
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поглощение излучения в материале. Закон Ламберта-Бугера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Закон Ламберта - Бугера (или Буге́ра - Ла́мберта)[10] определяет ослабление параллельного монохроматического пучка света при распространении его в поглощающей среде. Закон Ламберта – Бугера выражается следующей формулой: I out= I in×exp(- a · l) = I 0×(1- R)×exp(- a · l) (2.3.1а) или, для основания десятичных логарифмов, I out= I in 10 - k l = I 0×(1- R)×10 - k l. (2.3.1б) Здесь a и k - натуральный и десятичный коэффициенты поглощения соответственно. Таким образом, tint = I out / I in.= exp(- a · l) = 10 - k l; отсюда a = -ln t int·/ l (2.3.2а) и k = -lg t int·/ l, (2.3.2б) так что a = k ×2.3026. Коэффициент поглощения a или k является характеристикой материала как такового, а не конкретного образца, так как не зависит ни от толщины образца, ни от потерь на отражение; он является лишь функцией длины волны или частоты (см. ниже). Обычно используемая размерность этого коэффициента для бесцветных материалов – см-1 (для цветных оптических стекол – мм-1). Уравнения (2.3.1а) или (2.3.1а) закона Ламберта – Бугера служат математической основой для обработки экспериментальных данных о потерях энергии излучения в образцах той или иной толщины. Знание значения коэффициента поглощения a или k позволяет легко рассчитать коэффициент внутреннего пропускания образца любой толщины. Согласно найденному позднее закону Бера,[11] коэффициенты поглощения a и k растворов поглощающих веществ могут быть представлены в виде a = χ a ´ C, и k = χ k ´ C, где C - концентрация поглощающего вещества и χ a или χ k – удельный коэффициент поглощения (натуральный или десятичный соответственно) этого вещества, который предполагается независимым от концентрации. Объединение закона Ламберта – Бугера с законом Бера привело к уравнениям
и
которые называются поэтому законом Ламберта – Бугера – Бера. Этот объединенный закон достаточно широко используется не только для растворов, но и для твердых материалов (например, стекол), содержащих красящие примеси или активаторы:
В литературе иногда встречаются утверждения, что в некоторых случаях закон Ламберта – Бугера не соблюдается. Это утверждение на самом деле подменяет понятия, так как речь в этих случаях идет не о нарушениях базового закона Ламберта – Бугера (2.3.1а,б), который для изотропных безградиентных сред справедлив всегда, а о нарушениях лишь объединенного закона Ламберта – Бугера – Бера (2.3.3) из-за несоблюдения такой его составляющей, как закон Бера, для которого действительно характерны многочисленные отклонения в случаях, когда концентрация C превышает некоторое пороговое значение. Через значения a или k, найденные с помощью закона Ламберта – Бугера (2.3.1а,б), легко вычисляется безразмерный показатель поглощения k:
В случае слабого рассеяния малыми частицами закон рассеяния имеет вид, аналогичный закону Ламберта-Бугера (2.3.1а,б). Поэтому в практике производства бесцветных оптических стекол при описании интенсивности светового потока, прошедшего через слой материала, пользуются термином «коэффициент ослабления m», который определяется суммой m = k + s, (2.3.5) где s -коэффициент рассеяния. Для бесцветных оптических стекол значения s, как правило, много меньше k, и поэтому m ≈ k. Однако точные значения a, k или m не могут быть вычислены из эксперимента прямо с помощью соотношений (2.3.2а,б), так как в эксперименте измеряется не коэффициент внутреннего пропускания t int, а коэффициент внешнего пропускания t, зависящий от потерь на отражение (см. соотношение (2.1.3)). Для пластины из поглощающего материала мы получаем, пренебрегая многократным отражением: I = I out×(1 -R) = I 0 ×(1- R)2×exp(- a × l) = I 0 ×(1- R)2×10 - k l и t = I / I 0 = (1- R)2×exp(- a × l) = (1- R)2×10 - k l. Иногда для оценочных расчетов влиянием отражения пренебрегают, приравнивая коэффициент внешнего пропускания t коэффициенту внутреннего пропускания t int и используя его для расчета коэффициента поглощения по закону Ламберта – Бугера. Вносимая таким упрощением ошибка очень сильно зависит от показателя преломления материала. Для оконного стекла и оптических стекол типа крон с показателем преломления порядка 1.5 значение R составляет около 0.04 и соответственно t» 0.92 t int, что для грубых оценок еще допустимо. Однако для материалов с показателем преломления порядка 2.0 ситуация меняется: R» 0.11 и соответственно t» 0.79 t int, что неприемлемо. Поэтому для вычисления более точных значений a или k из экспериментальных данных о коэффициенте внешнего пропускания плоскопараллельной пластины следует использовать соотношения a = (1/ l)´[2ln(1- R) - ln t ] (2.3.6а) и k = (1/ l)´[2lg(1- R) - lg t ]. (2.3.6б) При углах падения, близких к нормали, значения коэффициента отражения R, необходимые для использования выражений (2.3.6а,б) в расчетах, могут быть вычислены с помощью соотношений (2.2.2а,б) или (2.2.3). Однако при этом вводится дополнительная погрешность, обусловленная тем, что при любом способе подготовки поверхности образца (кроме случая поверхности свежего скола, приготовленного в высоком вакууме) структура и даже состав поверхностного слоя несколько отличаются от свойственных объему материала. Прямое измерение коэффициента отражения не только удваивает объем измерений, но также увеличивает погрешность, поскольку ошибка его измерения, как правило, выше, чем ошибка измерения коэффициента пропускания. В качестве удобных практических характеристик потерь излучения в образцах используются также такие величины, как оптическая плотность D = -lg t и ее аналог для основания натуральных логарифмов, A = -ln t. Английский термин absorbance (по смыслу - поглощательная способность), используемый для обозначения последней величины, не имеет устоявшегося эквивалента в русской научной терминологии. Как видно, оптическая плотность D и поглощательная способность A зависят и от потерь на отражение, и от толщины образца. Таким образом, они являются характеристиками только конкретного образца (пластины), а не материала как такового. D = -lg t = -2lg (1- R) + k × l = DR + k × l (2.3.7а) и A = -ln t = -2ln (1- R) + a × l = AR+ + a × l, (2.3.7б) где DR и AR – поправки на отражение от двух поверхностей пластины, равные -2lg (1- R) и -2ln (1- R) соответственно. Для случая нормального падения луча из вакуума или воздуха
и
Можно устранить нежелательное влияние свойств поверхности образца, отличающихся от свойств объемного материала, на рассчитываемые значения коэффициентов поглощения (или ослабления), если использовать для измерений два образца разной толщины с одинаково приготовленными поверхностями. Поскольку для таких образцов поправки на отражение одинаковы, то разности их поглощающей способности или оптической плотности никак не связаны с эффектами их поверхностей: A 2 - A 1 = a ×(l 2 - l 1) и D 2 - D 1 = k ×(l 2 - l 1). Отсюда значения коэффициентов поглощения определяются очень простыми соотношениями: a = (A 2 - A 1) / (l 2 - l 1) (2.3.10а) и k = (D 2 - D 1) / (l 2 - l 1) (2.3.10б) Поэтому использование двух образцов разной толщины с последующим расчетом коэффициента поглощения по формулам (2.3.10а,б) представляет собой наиболее надежный метод его вычисления на основе закона Ламберта – Бугера. Следует, однако, понимать, что, независимо от конкретного пути вычисления, практическая применимость закона Ламберта – Бугера для таких вычислений ограничена областью не слишком сильного поглощения. Ясно, что когда оптическая плотность даже самого тонкого образца, который удается приготовить, превышает значения, допускаемые применяемым спектрофотометром, то измерения становятся невозможными. Однако и при не столь больших значениях оптической плотности (обычно от ~2.3 и выше), вычисление коэффициента поглощения по закону Ламберта – Бугера на основе прямых измерений пропускания становится нерациональным из-за резкого возрастания погрешности измерений. Для вычисления наиболее точных значений a или k из экспериментальных данных о коэффициенте внешнего пропускания следует учитывать и упоминавшееся выше явление многократного отражения в плоскопараллельной пластине. Существует ряд вариантов формул для описания вклада многократного отражения, различающихся в зависимости от того, сколько членов ряда последовательных отражений учитывается. Укажем здесь две из них. При пренебрежении возможностью интерференции в полностью прозрачной плоскопараллельной пластине ее суммарный коэффициент отражения R tot с учетом многократного отражения дается формулой R tot = 2 R /(1 + R). (2.3.11) Натуральный коэффициент поглощения пластины с учетом многократного отражения может вычисляться с помощью формулы
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

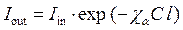 (2.3.3а)
(2.3.3а) (2.3.3б)
(2.3.3б)
 . (2.3.4)
. (2.3.4)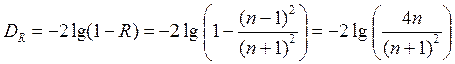 (2.3.8)
(2.3.8) (2.3.9)
(2.3.9) . (2.3.12)
. (2.3.12)


