
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое уравнение дисперсии комплексной диэлектрической проницаемости в современной науке. Модификация аналитической модели Друде.Содержание книги
Поиск на нашем сайте 4.2.1. Некоторые формальные преобразования При дальнейшей модификации форм записи дисперсионного уравнения для комплексной диэлектрической проницаемости в варианте Друде было прежде всего принято во внимание, что отношение 4 p N j e2 / m, стоящее в уравнениях (4.1.2) и (4.1.3а-в) перед дробью Далее, вид уравнений (4.1.3а) и (4.1.4б) предполагает, что суммирование ведется по всем видам осцилляторов, свойственных тому или иному веществу. Для целей применения дисперсионного уравнения для комплексной диэлектрической проницаемости к практическим задачам обработки экспериментальных данных это не совсем удобно, так как обрабатываемые данные обычно относятся к ограниченному спектральному диапазону, охватывающему положения лишь части осцилляторов. Поэтому модель Друде была модифицирована путем выделения суммы вкладов для K наиболее высокочастотных осцилляторов, собственные частоты wk которых чрезвычайно удалены от анализируемого спектрального диапазона:
Поскольку
которая представляет собой высокочастотную диэлектрическую проницаемость и которую принято обозначать символом осциллятора Sj, уравнение модели Друде принимает наиболее употребительную сейчас компактную форму:
Действительная и мнимая части комплексной диэлектрической проницаемости при такой форме записи модели Друде приобретают вид
и
Соответственно вышеупомянутое уравнение (4.1.4б) также было преобразовано в
оно нередко встречается в литературе. 4.2.2. Современное истолкование физического смысла параметров классической аналитической модели Друде. Как уже отмечалось выше, в диэлектрическую проницаемость при любых частотах входят не только вклады электронных возбуждений, на которые ориентированы уравнения (4.1.2), (4.1.3а) и (4.1.4б), но и вклады колебательных возбуждений. Кроме того, появление квантовой теории указало на целесообразность модификации некоторых величин, входящих в выражение для интенсивности осцилляторов Sj в классической модели, и для случая электронных переходов. Поэтому стало необходимым произвести некоторый пересмотр выражения для интенсивности Sj в уравнениях (4.2.1а-в) с учетом его зависимости от типа оптических возбуждений. Случай электронных переходов (ВУФ, УФ или видимый диапазон). Как следует из квантовомехянического рассмотрения, при взаимодействии электрона и кванта света с частотой, соответствующей частоте оптического возбуждения электрона, переход последнего на возбужденный уровень происходит не со стопроцентной вероятностью. Поэтому в числитель выражения для интенсивности Sj потребовалось ввести вероятность оптического перехода fj, нередко называемую также термином «сила осциллятора».[14] Далее, нужно было учесть, что поведение электрона в твердом теле определяется эффективной массой m * j, зависящей от свойств материала и вида перехода (а не массой свободного электрона, как в исходных моделях Друде и Лоренц-Лорентца). Поэтому для электронных переходов
Случай колебательных переходов (ИК диапазон). Здесь нужно учесть, что, в отличие от случая электронов, осциллятор включает как минимум две частицы, сравнительно близкие по массе. Поэтому его поведение определяется их приведенной массой M, задаваемой выражением
Далее, нужно учесть, что заряды частиц (атомов или ионов) обычно характеризуются относительными эффективными зарядами Zj, выражаемыми в долях заряда свободного электрона (то есть абсолютный заряд атома или иона равен произведению Zj × e). Как и в случае электронов, нужно также ввести вероятности оптических переходов fj. Поэтому для колебательных переходов
Таким образом, формы записи аналитической модели Друде в виде уравнений (4.1.2а-с) и (4.1.3а), а также форма записи аналитической модели Лоренц-Лорентца в виде уравнения (4.1.8) фактически не подходят для описания дисперсии диэлектрической проницаемости в области фундаментальных колебательных возбуждений в ИК диапазоне. Форма записи модели Друде в виде уравнений (4.2.1а-в) не претерпевает внешних изменений в зависимости от вида оптических возбуждений, но при анализе численных данных с помощью этих уравнений следует помнить о различии расшифровки символа Sj для разных видов оптических возбуждений. Классическое дисперсионное уравнение для комплексной диэлектрической проницаемости в таком осовремененном варианте Друде широко использовалось и продолжает успешно использоваться для количественного описания ИК спектров подавляющего большинства кристаллов (подробный перечень таких работ можно найти в [8]). В частности, на использовании этого уравнения основан широко известный метод дисперсионного анализа спектров кристаллов [19], широко обсуждаемый в [8] и рассматриваемый ниже в параграфе 6.2. 4.2.3. Контуры максимумов оптических постоянных, задаваемые классической аналитической моделью Друде. Рассмотрим теперь контуры максимумов действительной и мнимой частей комплексной диэлектрической проницаемости, показателя преломления, показателя поглощения и коэффициента поглощения, задаваемые уравнениями (4.2.1а-в). На рис. 14 показаны контуры действительной и мнимой частей комплексной диэлектрической проницаемости e¢(w) и e¢¢(w), создаваемые единственным осциллятором с частотой w 0.
Рис. 14. Контуры резонансов действительной и мнимой частей комплексной диэлектрической проницаемости e¢(w) и e¢¢(w), создаваемые осциллятором с частотой w 0 и значениями относительной интенсивности S / w 02 и коэффициента затухания g / w 0, равными 0.2 и 0.0175 соответственно. Можно видеть, что контур e¢¢(w) практически симметричен относительно w 0,[15] тогда как контур e¢(w) резко асимметричен и имеет область отрицательных значений. Следует обратить также внимание, что вид контура e¢(w) зависит (в отличие от контура e¢¢(w)) и от значения e ¥. При переходе от теоретического случая e ¥ = 1 (в реальности – для газов) к случаю твердого тела с e ¥ = 2.25 (что соответствует квадрату значения показателя преломления 1.5, типичного для оптических стекол типа крон в видимой области) контур e¢(w) становится не столь резким. Кроме того, в областях частот, удаленных от минимума, появляется диэлектрическая «подкладка» (e¢(w) > 0). Поскольку именно твердые тела, а не газы, представляют основной интерес как оптические материалы, то дальнейшие иллюстрации контуров будут даваться для случая e ¥ = 2.25. На рис. 15 показаны контуры показателя преломления n(w) и показателя поглощения k(w), создаваемые тем же осциллятором при e ¥ = 2.25.
Рис. 15. Контуры n(w) и k(w) вблизи частоты w 0 единственного осциллятора (J = 1). Относительные значения других параметров: S / w 02 = 0.20 и g / w 0 = 0.0175. Можно видеть, что контур k(w), в отличие от контура e¢¢(w), несимметричен и слегка смещен относительно w 0. Контур n(w), подобно контуру e¢(w), резко асимметричен, но имеет не область отрицательных значений, а область 0 < n(w) < 1. На рис. 16 и 17 показано, как влияет значение коэффициента затухания g на вид контуров n(w) и k(w). Можно видеть, что с увеличением g ширина контуров n(w) и k(w) существенно возрастает. Это и неудивительно, поскольку в классической модели коэффициент затухания – единственный фактор, определяющий полуширину полосы. Рис. 18 показывает ход частотных зависимостей n(w) и k(w), задаваемых двумя осцилляторами с достаточным промежутком между ними. Для удобства сравнения с приведенным выше рис. 13 значения частоты отложены справа налево. Видно, что модель двух осцилляторов достаточно хорошо воспроизводит качественную картину нормальной дисперсии реального материала.
Рис. 16. Изменение контуров максимумов n(w) вблизи частоты w 0 единственного осциллятора при вариации значений коэффициента затухания. Значения S / w 02 и
Рис. 17. Изменение контуров максимумов k(w) вблизи частоты w 0 единственного осциллятора при вариации значений коэффициента затухания. Значения S / w 02 и
Рис. 18. Частотные зависимости n(w) и k(w), задаваемые двумя осцилляторами с собственными частотами 700 и 1300 см-1. Перейдем далее к контуру максимума размерного коэффициента поглощения a (w). Согласно уравнению (4.2.1в),
а размерный коэффициент поглощения a (w) связан с безразмерным показателем поглощения k (w) соотношением a (w) · = 2 k (w)× w / c, где c - скорость света. Поэтому уравнение для a (w) принимает вид
Для одиночной линии вблизи ее максимума (J = 1) и при n(w)» 1 (случай газов) это выражение, прямо следующее из (4.2.1в), эквивалентно описанному ранее (см. параграф 3.3.2) лоренцеву контуру (3.1.7). Поэтому понятие «лоренцев контур» в его широком смысле относят также и к контурам максимумов мнимой части диэлектрической проницаемости (4.2.1в). Для демонстрации возможности свести уравнение (4.2.2) к ранней формуле лоренцева контура (3.1.7) рассмотрим участок контура вблизи его центра, вводя приближение w» w 0 и принимая J = 1 и n(w)» 1. Тогда w 0+ w » 2 w 0 и w 20- w 2» 2 w 0 (w 0- w ). Отсюда получаем:
и далее
При точном равенстве w = w 0 это выражение принимает вид
Тогда
При замене символов g = G, a = I и a max(w 0) = I 0 это выражение эквивалентно упрощенному лоренцеву контуру (3.1.7), выведенному в конце XIX века:
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 702; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , фактически представляет собой абсолютную интенсивность j -го осциллятора (оптического перехода), которую удобно обозначить собственным символом S j = 4 p N j e2 / m. Такая замена отношения 4 p N j e2 / m на символ одной переменной Sj была тем более уместна ввиду того, что в диэлектрическую проницаемость при любых частотах входят, строго говоря, вклады не только электронных возбуждений (как предполагают формы записи уравнений (4.1.2), (4.1.3а) и (4.1.4б), содержащие в явном виде заряд и массу электрона), но и колебательные, для которых параметры, входящие в отношение перед дробью
, фактически представляет собой абсолютную интенсивность j -го осциллятора (оптического перехода), которую удобно обозначить собственным символом S j = 4 p N j e2 / m. Такая замена отношения 4 p N j e2 / m на символ одной переменной Sj была тем более уместна ввиду того, что в диэлектрическую проницаемость при любых частотах входят, строго говоря, вклады не только электронных возбуждений (как предполагают формы записи уравнений (4.1.2), (4.1.3а) и (4.1.4б), содержащие в явном виде заряд и массу электрона), но и колебательные, для которых параметры, входящие в отношение перед дробью  .
. , то вклады таких осцилляторов в диэлектрическую проницаемость при текущих частотах w анализируемого спектрального диапазона являются почти бездисперсионными и соответственно
, то вклады таких осцилляторов в диэлектрическую проницаемость при текущих частотах w анализируемого спектрального диапазона являются почти бездисперсионными и соответственно  . Это позволяет заменить их сумму (вместе с единицей) одной константой:
. Это позволяет заменить их сумму (вместе с единицей) одной константой: ,
,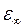 . Тогда при переопределении числа членов суммы как J=J – K, а также с учетом сказанного выше о замене отношения 4 p Nj e2 / m интенсивностью j -го
. Тогда при переопределении числа членов суммы как J=J – K, а также с учетом сказанного выше о замене отношения 4 p Nj e2 / m интенсивностью j -го (4.2.1а)
(4.2.1а)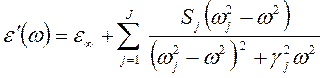 (4.2.1б)
(4.2.1б) . (4.2.1в)
. (4.2.1в) ; (4.2.2)
; (4.2.2) . (4.2.3а)
. (4.2.3а) , т. е.,
, т. е.,  .
. . (4.2.3б)
. (4.2.3б)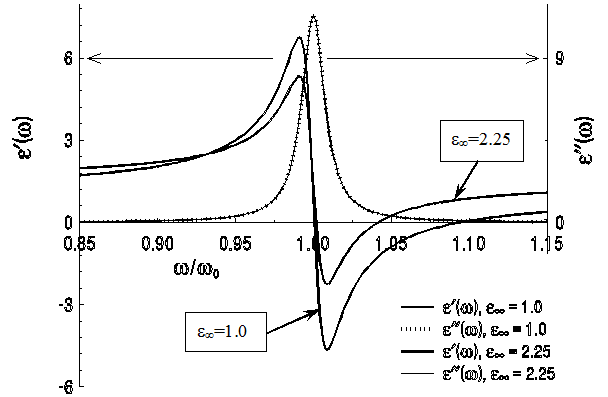




 ,
, . (4.2.4)
. (4.2.4)
 .
. .
. , и поэтому можно выразить
, и поэтому можно выразить  через
через  :
: .
. .
.


