
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды и механизмы поглощения электромагнитного излучения в различных спектральных диапазонахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Здесь следует, прежде всего, напомнить, что электромагнитное излучение принято делить на виды по частотным диапазонам (см. табл. 1). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Каждый из этих частотных диапазонов характеризуется своими специфическими процессами поглощения излучения, кратко перечисленными в последней колонке табл. 1. Понятия, упоминаемые в последней колонке табл. 1, предполагаются, как правило, известными в общих чертах из дисциплины «Физика твердого тела» (некоторые из них также детализируются позднее в специальных дисциплинах). Поэтому здесь даются лишь краткие пояснения некоторых терминов и принципиальных соотношений. Как будет показано ниже в главах 3 и 4, спектры коэффициента поглощения и показателя преломления (а значит, и коэффициента отражения) взаимосвязаны и располагаются почти в одних и тех же областях частот или длин волн. Поэтому все то, что говорится ниже о происхождении спектров поглощения в тех или иных областях частот, в равной мере относится и к происхождению остальных упомянутых видов оптических спектров. При поглощении кванта электромагнитного излучения электрон или атомная группа приобретает дополнительную энергию, которая вызывает переход системы с низшего энергетического уровня (обычно основного) на более высокие (возбужденные). Энергии переходов квантуются, поэтому переходы носят резонансный характер (то есть они совершаются только тогда, когда энергия или частота кванта приближается к энергии или частоте перехода). Таблица 1. Частотные диапазоны электромагнитного излучения и соответствующие им процессы поглощения
По физической природе возбуждаемых систем и соответствующих им оптических переходов спектры поглощения делятся на три типа: спектры электронных возбуждений, колебательные спектры и вращательные спектры. А. Спектры электронных возбуждений. Эти спектры нередко называются для краткости просто электронными оптическими спектрами (не путать с энергетическим спектром электронов в твердом теле или со спектрами фотоэлектронной эмиссии!). Они обусловлены переходами электронов валентных оболочек атомов на возбужденные электронные уровни. Наблюдаются для всех классов веществ. В твердых телах спектры электронных возбуждений в свою очередь подразделяются на два типа. А.1. Фундаментальные (или собственные) электронные спектры матрицы твердого тела. Механизмы формирования этих спектров обсуждаются ниже (см. параграф 1.2.1). Максимальные значения коэффициента поглощения в них достигают гигантских значений - до 106 см -1. Для материалов, прозрачных в видимом диапазоне (оптические стекла, кристаллы оксидов и галогенидов), фундаментальные электронные спектры занимают весь вакуумный ультрафиолетовый (ВУФ) и часть ближнего ультрафиолетового диапазона (см. таблицу), тем самым задавая их коротковолновый край собственного поглощения (см. ниже). Для ИК материалов (халькогенидные стекла, кристаллы кремния, германия, теллурида кадмия и др.) эти спектры смещаются в ближний УФ и видимый диапазоны. Соответственно коротковолновый край собственного поглощения таких материалов сдвигается к границе между видимым и ближним ИК диапазонами или целиком в ближний ИК диапазон. А.2. Спектры электронных переходов в валентных оболочках (а) атомов или ионов примесей, (б) атомов или ионов активаторов и (в) собственных точечных дефектов (если таковые присутствуют). Отдельные полосы поглощения или группы полос, соответствующие этим спектрам, могут наблюдаться в ближнем УФ, видимом и ближнем ИК диапазонах (см. табл. 1). Значения коэффициента поглощения в этих полосах сильно зависят от концентраций соответствующих атомов, ионов или дефектов. Более подробно эти спектры рассматриваются в одной из специальных дисциплин. Б. Колебательные спектры. Эти спектры обусловлены переходами атомных групп или ионов на возбужденные колебательные уровни. Наблюдаются для всех классов веществ, кроме веществ с чисто гомеополярными химическими связями. В твердых телах колебательные спектры в свою очередь подразделяются на несколько типов. Б.1. Фундаментальные спектры (или колебательные спектры первого порядка) матрицы твердого тела. Механизм формирования этих спектров обсуждается ниже (см. параграф 1.2.2). Максимальные значения коэффициента поглощения в них достигают значений порядка 104 см-1. Для веществ, состоящих из легких атомов (например, воды), фундаментальные колебательные спектры располагаются в высокочастотной части среднего ИК диапазона. Для оптических стекол и кристаллов фундаментальные колебательные спектры занимают не только средний, но и дальний ИК диапазоны (см. таблицу). Б.2. Многофононные колебательные спектры (или колебательные спектры второго, третьего и т.д. порядка) матрицы твердого тела. Эти спектры образуют системы полос поглощения последовательно убывающей интенсивности (см. ниже), которые могут простираться от высокочастотной части среднего ИК диапазона до видимого. Б.3. Колебательные спектры примесных групп или молекул (как фундаментальные, так и многофононные). В. Вращательные спектры. Они свойственны, как правило, только низкомолекулярным веществам (например, водяному пару), молекулы которых способны совершать вращения независимо друг от друга.[5] Эти спектры обусловлены переходами между различными вращательными уровнями. Поскольку для подавляющего большинства оптических материалов вращательные спектры нехарактерны, они не рассматриваются далее в данном разделе дисциплины. 1.2.1. Фундаментальное поглощение, обусловленное возбуждениями в твердых телах 1.2.1.1. Формирование электронных спектров твердого тела в одноэлектронном приближении Простейшая физическая модель, описывающая механизм формирования фундаментального электронного спектра поглощения твердого тела, дается так называемой одноэлектронной зонной теорией (или, точнее, зонной схемой, рассматриваемой в одноэлектронном приближении), которая разрабатывалась для описания свойств классических кристаллических полупроводников (см., например, [3]). Согласно этой схеме, иллюстрируемой рисунком 2, полностью заполненные валентные орбитали атомов матрицы твердого тела образуют, перекрываясь друг с другом, единую валентную зону разрешенных энергетических состояний электрона. На рис. 2 по оси абсцисс отложен так называемый волновой вектор. Значение волнового вектора характеризует волновое число (или энергию), а его ориентация – направление распространения электромаг-нитной волны или возбуждения в кристалле. Свободное движение электронов по валентной зоне невозможно только из-за отсутствия вакантных электронных состояний, в которые мог бы осуществиться переход. Орбитали следующей незаполненной электронной оболочки тех же атомов образуют, также перекрываясь друг с другом, единую пустую зону разрешенных энергетических состояний электрона. Эта вторая зона называется зоной проводимости. Электрон, достигший зоны проводимости за счет термического или оптического возбуждения, считается полностью утратившим связь с той орбиталью валентной зоны, с которой он был возбужден. Это означает, что такой электрон может беспрепятственно мигрировать по вакантным состояниям зоны под действием поля, тем самым обеспечивая электропроводность материала (отсюда и название этой зоны). Вакансия электрона, оставшаяся в валентной зоне, рассматривается как квазичастица с положительным зарядом, обозначаемая термином “дырка”, которая также может свободно мигрировать по этой зоне путем последовательного перескока электронов с заполненных орбиталей на эту вакансию.
Рис. 2. Простейшая зонная схема в одноэлектронном приближении. Пояснения в тексте.
Между валентной зоной и зоной проводимости располагается зона нереализуемых энергетических состояний электрона, которая так и называется – запрещенная зона (она обозначается символом Оптическое возбуждение с наименьшей возможной энергией соответствует переходу электрона с верхней границы (“потолка”) валентной зоны
где значение целого числа n определяется тем, являются соответствующие прямые переходы разрешенными (n = 1) или запрещенными (n = 3). Картина, иллюстрируемая рисунком 2, представляет собой предельно упрощенный случай двух зон с “плоскими” (то есть не зависящими от волнового вектора) границами. Реальные кристаллы могут иметь несколько перекрывающихся между собой валентных зон и зон проводимости, число которых и форма их границ зависят от симметрии решетки (эта симметрия определяет и конкретную структуру сплошного спектра при энергиях фотона
При наличии больших концентраций примесей или дефектов или при разупорядочении решетки границы валентной зоны и зоны проводимости размываются за счет появления “хвостов” локализованных состояний, простирающихся в запрещенную зону (см., например, [5,9]). Это, естественно, приводит и к размытию края поглощения. Наиболее типичная форма края поглощения
где Одноэлектронное приближение, кратко охарактеризованное выше, удовлетворительно описывает оптические свойства только классических полупроводников с достаточно малой шириной запрещенной зоны и очень высокими значениями статической диэлектрической проницаемости (кремний, германий, GaAs, InSb и т.п.). Для материалов с большей шириной запрещенной зоны и соответственно более низкой статической диэлектрической проницаемостью электростатическое взаимодействие электрона и дырки не утрачивается полностью. В результате возникает связанное электронно-дырочное состояние, обозначаемое термином “экситон” и ведущее себя в первом приближении как водородоподобный атом с дыркой вместо ядра и квантованными уровнями энергии электрона (см., например, [6]). Экситонные возбуждения проявляются в спектре поглощения в виде узких линий или серий таких линий, которые в большинстве случаев (например, в спектрах хлорида меди, щелочногалоидных кристаллов и твердых инертных газов) располагаются в области края межзонного поглощения. Однако полосы экситонных переходов могут наблюдаться и при энергиях фотона 1.2.1.2. Фундаментальное электронное поглощение в диэлектриках Для диэлектриков, в частности, оксидов, которые представляют для нас особый интерес как оптические материалы, механизмы формирования фундаментальных электронных спектров более сложны и гораздо менее изучены. Причиной является тот факт, что вследствие низкой статической диэлектрической проницаемости диэлектриков для них характерно очень сильное электронно-дырочное взаимодействие, благодаря которому системы экситонных полос играют в электронных спектрах диэлектриков гораздо большую роль, чем в случае полупроводников. Примером может служить УФ спектр оптических постоянных MgO, показанный на рис. 3. Видны интенсивные острые пики, характерные для экситонных переходов.
Рис. 3. Оптические постоянные кристалла MgO в УФ диапазоне [10].
Среди оксидов элементов III-V групп периодической системы, способных быть основой оптических стекол, только кремнезем (как кристаллический, так и стеклообразный) изучен достаточно подробно (см., например, [11]) с точки зрения его экспериментального электронного спектра. Спектры оптических постоянных стеклообразного SiO2 в ВУФ диапазоне представлены на рис. 4. Однако до сих пор отсутствует ясность в отнесении наблюдаемых четырех максимумов поглощения (отражения) кремнезема к тем или иным типам оптических возбуждений. В период, предшествовавший написанию монографии [11], большинство исследователей считало, что первые два максимума этого спектра при 10.4 (для стекла 10.2) и 11.5 эВ - это экситонные полосы со сложной внутренней структурой, а два следующих более широких максимума при 14.5 и 17.5 эВ - это уже детали спектра прямых межзонных переходов. Позднее ряд исследователей пришел к заключению (см. [11]), что и третий максимум при 14.5 эВ имеет экситонную природу. Наконец, в [12] был выполнен детальный полуэмпирический расчет электронного спектра кремнезема, который показал, что, по-видимому, все четыре наблюдаемых максимума имеют экситонную природу и что, таким образом, прямые
Рис. 4. Спектры оптических постоянных стеклообразного SiO2 в ВУФ диапазоне [8].
межзонные переходы вообще не играют существенной роли в формировании этого спектра. Таким образом, край собственного поглощения кремнезема задается длинноволновым крылом экситонного максимума с центром около 10.4 эВ для кристалла и 10.2 эВ для стекла, который сформирован наложением нескольких экситонных пиков разного происхождения [11]. Хотя при этом край поглощения может чисто эмпирически описываться правилом Урбаха (1.2.3), параметры последнего в данном случае не имеют прямой связи с природой происходящих процессов. 1.2.2. Фундаментальные колебательные спектры 1.2.2.1. Колебательные уровни двухатомной молекулы Простейшим вариантом вибратора (атомной системы, способной совершать колебания) является двухатомная молекула. Частота ее колебания определяется в первую очередь степенью жесткости химической связи между атомами и массами атомных ядер (подробнее см. ниже параграфы 4.1-4.2). Колебательные состояния молекулы квантуются, что порождает систему дискретных колебательных уровней. При достаточно низких температурах молекула, как правило, находится на основном (наинизшем) колебательном уровне и может переходить на более высокие уровни за счет поглощения энергии кванта ИК излучения. Если бы колебание было строго гармоническим (то есть полностью симметричным относительно центра равновесия), то классическая (без учета квантования уровней) кривая потенциальной (внутренней) энергии молекулы как функции отклонения межатомного расстояния от равновесного задавалась бы уравнением параболы. Колебания реальной молекулы характеризуются определенной степенью ангармонизма, в результате чего эта зависимость лучше описывается хорошо известной эмпирической кривой Морзе (см. рис. 5), задаваемой таким уравнением:
Рис. 5. Кривые U(x) для колебаний двухатомной молекулы. 1- идеализированный случай строго гармонических колебаний, 2 - кривая Морзе для колебаний реальной молекулы. Основные обозначения соответствуют приведенным для уравнения (1.2.4). Символом
U(x) = De [1 - exp -(x - re)]2, (1.2.4) где x - межатомное расстояние, re - равновесное межатомное расстояние, De - энергия диссоциации в равновесном состоянии. Из рис. 5 видно, что нарастание потенциальной энергии при растяжении химической связи происходит заметно медленнее, чем при таком же ее сжатии. При дальнейшем растяжении химической связи потенциальная энергия молекулы стремится к нулю, что соответствует ее полной диссоциации на атомы. Кривая Морзе представляет собой лишь простейшую, крайне идеализированную иллюстрацию явления. Реальные колебательные процессы, особенно в твердых телах, требуют более подробного рассмотрения. 1.2.2.2. Фундаментальные колебательные возбуждения в твердых телах Колебательное возбуждение в твердом теле носит название “фонон”. В кристалле фонон - это делокализованное состояние, представляющее собой плоскую волну возбуждения, пробегающую через всю его решетку (см., например, [2]). В простейшем случае ионных кристаллов фонон представляет собой взаимное смещение катионной подрешетки как целого и анионной подрешетки как целого. Для кубических кристаллов существует только одна собственная фононная частота Для веществ с заметной степенью ковалентности химической связи колебательные процессы оказываются намного сложнее. Опуская здесь рассмотрение всего комплекса вопросов влияния симметрии самой молекулы или структурной группы при усложнении ее трехмерной структуры (см., например, [7]) и симметрии взаимного расположения таких групп в элементарной ячейке кристалла,[6] перейдем сразу к важному для дальнейшего изложения дисциплины общему случаю наращивания полимерной цепочки от стадии двухатомной молекулы (мономера) до цепочки квазибесконечной длины (см., например, [14]). При присоединении третьего атома к этой двухатомной молекуле (то есть при образовании линейной трехатомной молекулы, содержащей два вибратора) происходит расщепление прежнего единственного колебания на два с частотами несколько меньше и несколько больше собственной частоты колебания с частотой Однако отнюдь не все эти состояния способны принимать участие в поглощении излучения. Для квазибесконечных упорядоченных структур (кристаллы) существует правило отбора по трансляционной симметрии, согласно которому только состояние, лежащее на краю колебательной зоны, способно воспринять энергию кванта излучения. Иначе говоря, вместо одной полосы поглощения в спектре исходного мономера, соответствующей колебанию с частотой Для трехмерной полимерной структуры кристалла картина существенно усложняется. Общее число возможных колебаний составляет уже 3N - 3, причем возникают различные колебательные зоны. Число и взаимное расположение этих зон (а значит, и полос поглощения, соответствующих краям этих зон) на шкале частот определяются закономерностями, которые выводятся, исходя из собственной симметрии структурных групп, формирующих каркас полимера, и симметрии их взаимного расположения в элементарной ячейке кристалла (или в области локализации фонона - см. ниже). Эти вопросы подробно рассматриваются лишь в специальной литературе (например, [13]) и в данном разделе дисциплины не затрагиваются. При не слишком сложной структуре материала число полос фундаментальных колебаний в ИК спектре его поглощения (отражения) может составлять 6-8 (как это имеет место, например, в случае кремнезема - см. рис. 6). Для кристаллов с особо сложными элементарными ячейками общее число полос фундаментальных колебаний в их спектрах может достигать нескольких десятков. Интенсивность любого колебательного возбуждения зависит от того, насколько изменяется дипольный момент атомной группы или молекулы в акте колебания. Существуют виды колебаний, при которых дипольный момент вообще остается постоянным (меняется лишь поляризуемость). Такие колебания не могут возбуждаться ИК излучением и соответственно не могут давать полос поглощения в ИК спектре (о них принято говорить, что они неактивны в ИК спектре). Место таких колебаний в общей систематике колебательных процессов и методы их экспериментального выявления не рассматриваются в данном разделе дисциплины. Особый случай представляют колебательные возбуждения в стеклах и других неупорядоченных материалах. Для них отменяется правило отбора по трансляционной симметрии и, что еще более важно, фононы оказыва-
Рис. 6. Спектры оптических постоянных стеклообразного SiO2 в ИК диапазоне [8].
ются локализованными в областях микроскопических размеров [8]. Дополнительные эффекты, обусловливаемые этими обстоятельствами, кратко описываются ниже в параграфах 5.2-5.3. 1.2.3. Многофононное поглощение С некоторой достаточно малой вероятностью поглощение ИК излучения может происходить и при частотах, либо примерно кратных частоте какого-либо фундаментального колебания (это - так называемые обертоны данного колебания), либо равных сумме двух или более частот различных фундаментальных колебаний (это - так называемые составные частоты). Возникающие вследствие этого спектры поглощения называются многофононными спектрами (или колебательными спектрами второго, третьего и т. д. порядка). Первый, второй и т. д. обертоны фундаментального колебания с частотой
Многофононное поглощение имеет большое значение для практического применения оптических материалов по следующим причинам: · Именно многофононное поглощение, а не коротковолновое крыло ближайшей фундаментальной полосы поглощения, определяет длинноволновую границу области прозрачности чистых оптических материалов. В качестве примера на рис. 7 показан собственный многофононный спектр кварцевого стекла из [15]. Это многофононное поглощение ограничивает область прозрачности кварцевого стекла длиной волны не свыше 4.5-4.6 мкм (тогда как длина волны ближайшего фундаментального колебания составляет 8.5 мкм). · Многофононное поглощение примесной воды (молекулы H2O и гидроксильные группы OH) в промышленных стеклах, наблюдаемой в ближнем ИК диапазоне (см., например, ниже рис. 27), влияет на радиационный теплоперенос в расплавах стекол и вызывает тушение люминесценции в лазерных стеклах.
Рис. 7. Собственный многофононный спектр кварцевого стекла [15].
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.014 с.) |


 – см. рис. 2). Между полупроводниками и диэлектриками нет качественного различия, и отнесение материала к одному из этих классов целиком определяется значением ширины запрещенной зоны. Если ширина запрещенной зоны достаточно велика (условно принятая граница отвечает неравенству
– см. рис. 2). Между полупроводниками и диэлектриками нет качественного различия, и отнесение материала к одному из этих классов целиком определяется значением ширины запрещенной зоны. Если ширина запрещенной зоны достаточно велика (условно принятая граница отвечает неравенству 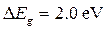 ), то материал обычно относят к диэлектрикам; если она ниже этой границы, то материал рассматривают как полупроводник.
), то материал обычно относят к диэлектрикам; если она ниже этой границы, то материал рассматривают как полупроводник. на низшую границу (“дно”) зоны проводимости
на низшую границу (“дно”) зоны проводимости 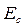 (стрелка 1 на рис. 2), энергия которого, естественно, равна
(стрелка 1 на рис. 2), энергия которого, естественно, равна  (
( , где h - постоянная Планка). Значения коэффициента поглощения
, где h - постоянная Планка). Значения коэффициента поглощения  для такого края в зависимости от частоты излучения описываются соотношениями общего вида
для такого края в зависимости от частоты излучения описываются соотношениями общего вида , (1.2.1)
, (1.2.1)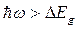 ). В частности, для ряда кристаллов зазор между потолком самой высоколежащей валентной зоны и минимумом какой-либо зоны проводимости, лежащим при другом значении волнового вектора, оказывается меньше, чем
). В частности, для ряда кристаллов зазор между потолком самой высоколежащей валентной зоны и минимумом какой-либо зоны проводимости, лежащим при другом значении волнового вектора, оказывается меньше, чем  . Поэтому становятся возможными так называемые непрямые (происходящие с изменением волнового вектора) оптические переходы при энергиях фотона
. Поэтому становятся возможными так называемые непрямые (происходящие с изменением волнового вектора) оптические переходы при энергиях фотона 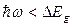 . Значения коэффициента поглощения
. Значения коэффициента поглощения 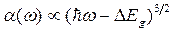 (1.2.2)
(1.2.2) , (1.2.3)
, (1.2.3) – константа, характеризующая сам материал, а также образец из него, приготовленный по определенной методике (технологии).
– константа, характеризующая сам материал, а также образец из него, приготовленный по определенной методике (технологии). , накладываясь на сплошной спектр прямых межзонных переходов [6].
, накладываясь на сплошной спектр прямых межзонных переходов [6].

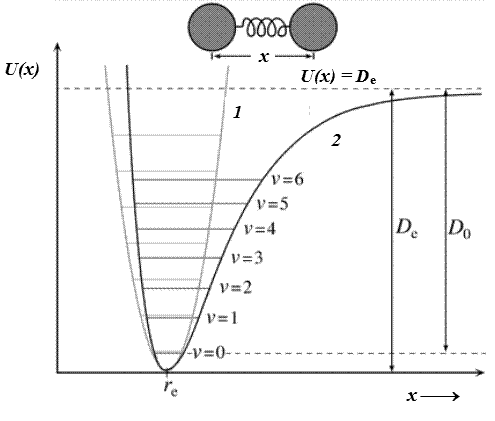
 обозначены номера колебательных уровней. D 0 – фактическая энергия диссоциации, соответствующая переходу с основного уровня (
обозначены номера колебательных уровней. D 0 – фактическая энергия диссоциации, соответствующая переходу с основного уровня ( ).
). , которой соответствует мощная полоса поглощения в среднем или дальнем ИК диапазоне.
, которой соответствует мощная полоса поглощения в среднем или дальнем ИК диапазоне. до
до  , где
, где  - полуширина этой зоны.
- полуширина этой зоны.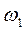 .
.
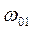 примерно соответствуют удвоенной, утроенной и т. д. частоте этого колебания (то есть относятся к спектрам второго, третьего и т. д. порядка соответственно) и поэтому обозначаются как
примерно соответствуют удвоенной, утроенной и т. д. частоте этого колебания (то есть относятся к спектрам второго, третьего и т. д. порядка соответственно) и поэтому обозначаются как  ,
,  и т. д. Точные значения частот обертонов на самом деле оказываются немного ниже за счет влияния ангармонизма. Различные составные частоты могут обозначаться как
и т. д. Точные значения частот обертонов на самом деле оказываются немного ниже за счет влияния ангармонизма. Различные составные частоты могут обозначаться как 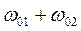 ,
, ,
,  и т.д.
и т.д.



