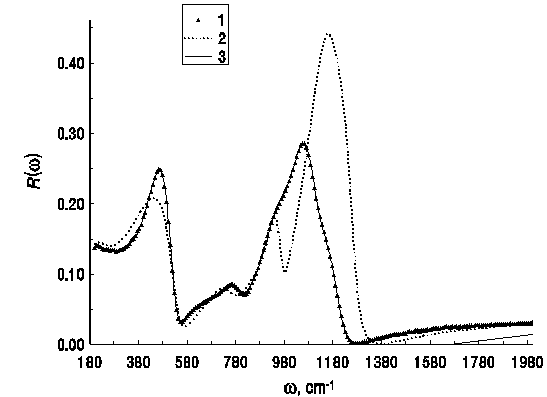Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод дисперсионного анализаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В отличие от метода Крамерса-Кронига, метод дисперсионного анализа может применяться как к спектру коэффициента отражения Впервые метод дисперсионного анализа был реализован в [19] для спектров отражения кристаллов на основе классической модели (4.2.1а-в), причем вариация параметров осуществлялась еще вручную методом проб и ошибок. В дальнейшем, естественно, был осуществлен переход к машинной вариации параметров по некоторому оптимальному алгоритму. В связи с этим потребовалось количественно характеризовать отклонения модельного спектра от экспериментального с помощью какой-либо функции невязки. Например, для случая анализа спектра отражения
где a и b - границы частотного диапазона, занимаемого анализируемым спектром. Можно видеть, что данная функция невязки представляет собой среднеквадратичную ошибку, усредненную по всему анализируемому спектру. Отсюда следует условие достижения наивысшего возможного качества подгонки анализируемого спектра:
где Принципиальная схема работы компьютерной программы дисперсионного анализа приведена на рис. 23. Несомненное достоинство метода дисперсионного анализа заключается в том, что и спектры оптических постоянных, и значения всех параметров полос сложного спектра рассчитываются, в отличие от метода Крамерса-Кронига, в ходе одной и той же вычислительной процедуры. Следовательно, погрешности расчета всех искомых величин определяются только погрешностью самой этой процедуры, то есть никакого суммирования погрешностей различных методов не происходит. Это преимущество метода дисперсионного анализа по сравнению с методом Крамерса-Кронига иллюстрируется схемой, представленной на рис. 24.
Рис. 23. Принципиальная схема работы компьютерной программы дисперсионного анализа. Цифры указывают последовательные номера выполняемых шагов.
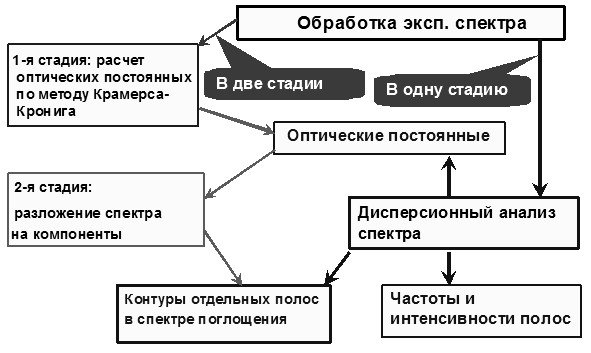
Рис. 24. Схема, сравнивающая виды и пути получения информации с помощью методов дисперсионного анализа и Крамерса-Кронига.
Важно также, что результаты применения метода дисперсионного анализа, в отличие от метода Крамерса-Кронига, практически нечувствительны к локальным ошибкам анализируемого спектра отражения. Существует множество различных версий метода дисперсионного анализа, различающихся как выбором конкретной модели дисперсии комплексной диэлектрической проницаемости (и соответственно пригодностью для того или иного класса веществ), так и алгоритмами минимизации функции невязки. В частности, была реализована и широко применяется версия метода дисперсионного анализа для стекол [8,16,23], использующая модель свертки (5.3.1а-в). Примеры качества аппроксимации экспериментальных спектров стекол, достигаемого с помощью метода дисперсионного анализа на основе модели свертки [8,16,23], приведены на рис. 25-27. На рис. 27 показан также результат разложения одного из этих спектров на спектральные компоненты (индивидуальные полосы).
Рис. 25. Аппроксимация ИК спектра отражения боросиликатного стекла. 1 – экспериментальный спектр (точки), 2 – модельный спектр, построенный по начальным приближениям параметров, 3 – модельный спектр после завершения аппроксимации.
Рис. 26. Процесс приближения модельного спектра к экспериментальному ИК спектру отражения стекла 33.4Na2O*66.6SiO2 [8] по мере увеличения числа циклов подгонки.
Рис. 27. Разложение спектра примесного поглощения гидроксильных групп и молекул воды в кварцевом стекле КУ1 на отдельные полосы поглощения.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , так и к спектру коэффициента поглощения
, так и к спектру коэффициента поглощения 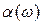 . В методе дисперсионного анализа той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных, является конкретная аналитическая модель дисперсии комплексной диэлектрической проницаемости. Она выбирается исследователем среди имеющихся моделей как наиболее подходящая для исследуемого материала. С помощью модели дисперсии комплексной диэлектрической проницаемости производится вычисление начального модельного спектра отражения или поглощения при произвольно взятых значениях параметров этой модели. Сущность вычислительной процедуры метода дисперсионного анализа состоит в минимизации отклонений модельного спектра от экспериментального путем итерационного процесса последовательной вариации всех параметров модели.
. В методе дисперсионного анализа той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных, является конкретная аналитическая модель дисперсии комплексной диэлектрической проницаемости. Она выбирается исследователем среди имеющихся моделей как наиболее подходящая для исследуемого материала. С помощью модели дисперсии комплексной диэлектрической проницаемости производится вычисление начального модельного спектра отражения или поглощения при произвольно взятых значениях параметров этой модели. Сущность вычислительной процедуры метода дисперсионного анализа состоит в минимизации отклонений модельного спектра от экспериментального путем итерационного процесса последовательной вариации всех параметров модели. удобно использовать [8] функцию невязки Q вида
удобно использовать [8] функцию невязки Q вида , (6.3.1)
, (6.3.1) , (6.3.2)
, (6.3.2) - случайная ошибка измерения.
- случайная ошибка измерения.