
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы количественной обработки экспериментальных оптико-спектроскопических данныхСодержание книги
Поиск на нашем сайте
Как видно из всего вышеизложенного, знание возможно более точных значений оптических постоянных материалов в возможно более широком диапазоне частот имеет большое научное и практическое значение. Однако при значениях показателя поглощения свыше 0.0001 прямое независимое измерение значений показателя преломления становится невозможным (слишком мало энергии излучения спектрального источника начинает проходить через измерительную призму). При значениях показателя поглощения свыше 0.001 становится невозможным и надежное измерение характеристик поглощения (коэффициент пропускания образца толщиной всего лишь 1 мм становится менее 10%). В этих условиях един-
Рис. 22. Сравнение контуров n(w) и k(w) вблизи частоты w 0 единственного осциллятора при значениях s / w 0, равных нулю (модель Друде) и 0.035 (модель свертки). Значения S / w 02, g / w 0 и
ственной надежно измеряемой оптической функцией становится энергетический коэффициент отражения, зависящий, согласно уравнениям (2.2.3) или (2.2.5а,б), от обеих оптических постоянных. Проблема, однако, заключается в том, что при обычном измерении коэффициента отражения исследователь получает для каждого конкретного значения частоты одно уравнение (например, уравнение вида (2.2.3)) с двумя неизвестными. Таким образом, задача не имеет решения без привлечения независимой дополнительной информации. Отсюда возникает необходимость либо в получении такой дополнительной информации чисто экспериментальным путем, либо в специальных вычислительных методах извлечения физически значимых и практически важных данных об оптических постоянных из стандартных «сырых» экспериментальных данных о коэффициенте отражения. Методы двух углов и двух поляризаций Для не слишком больших значений показателя поглощения Метод Крамерса-Кронига Метод Крамерса-Кронига базируется на использовании соотношения Крамерса-Кронига (3.1.5) для фазового угла. Существенно, что это соотношение предусматривает интегрирование от нуля до бесконечности, а экспериментальный спектр отражения
Для первого и третьего интегралов, соответствующих неизмеряемым спектральным диапазонам Например, вид
где C - константа, а показатель степени k подбирается в пределах 3 < k < 4. Уточнение вида модельных функций и значений их параметров производится с помощью привязочных точек, для которых значения фазового угла известны из независимых соображений (например, во всей области высокой прозрачности фазовый угол по определению равен нулю) или измерений. В литературе описано множество версий метода Крамерса-Кронига, различающихся выбором модельных функций, спектральной областью применения и степенью надежности вычисления значений оптических постоянных. Известно, что в целом результаты применения метода Крамерса-Кронига весьма чувствительны к локальным ошибкам анализируемого спектра отражения. Наличие таких ошибок может привести к получению ложных экстремумов в спектрах оптических постоянных. Значения фазового угла, полученные с помощью уравнения (6.2.1), используются вместе со значениями
и
Как и в случае двух предыдущих методов, получаемые с помощью метода Крамерса-Кронига результаты целиком ограничиваются спектрами оптических постоянных. Если исследователю нужно найти не только спектры оптических постоянных как таковые, но также значения частот и интенсивностей полос, перекрывающихся между собой в сложном спектре мнимой части диэлектрической проницаемости, он должен разложить этот спектр на такие индивидуальные полосы с помощью уже какого-то другого, независимого метода разложения. В этом случае итоговая погрешность расчета параметров полос будет равна сумме погрешностей метода вычисления оптических постоянных (в частности, метода Крамерса-Кронига) и метода разложения сложного спектра.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.100 (0.006 с.) |


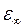 те же, что и на рис. 15.
те же, что и на рис. 15. существуют два разных метода прямого вычисления оптических постоянных из экспериментальных данных о коэффициенте отражения
существуют два разных метода прямого вычисления оптических постоянных из экспериментальных данных о коэффициенте отражения  (см., например, [24]). Оба они основаны на том, что уравнения Френеля позволяют получить при наклонном падении луча два разных значения
(см., например, [24]). Оба они основаны на том, что уравнения Френеля позволяют получить при наклонном падении луча два разных значения  ) погрешность расчета по порядку величины приближается к самим вычисляемым значениям оптических постоянных. Следовательно, эти методы непригодны для использования в широких диапазонах частот, включающих области фундаментального поглощения. Для таких областей были разработаны два других метода, свободные от ограничений по значениям показателя поглощения и предназначенные для обработки массивов значений
) погрешность расчета по порядку величины приближается к самим вычисляемым значениям оптических постоянных. Следовательно, эти методы непригодны для использования в широких диапазонах частот, включающих области фундаментального поглощения. Для таких областей были разработаны два других метода, свободные от ограничений по значениям показателя поглощения и предназначенные для обработки массивов значений  ).
). :
: 6.2.1)
6.2.1) и
и  , должны быть подобраны какие-то подходящие модельные функции
, должны быть подобраны какие-то подходящие модельные функции  и
и 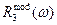 , задающие ожидаемую дисперсию
, задающие ожидаемую дисперсию  в этих диапазонах. Предполагаемый вид этих модельных функций и является той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных.
в этих диапазонах. Предполагаемый вид этих модельных функций и является той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных.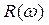 в области энергий свыше 30 эВ часто аппроксимируется степенной функцией вида
в области энергий свыше 30 эВ часто аппроксимируется степенной функцией вида
 для расчета спектров оптических постоянных с помощью формул
для расчета спектров оптических постоянных с помощью формул (6.2.2а)
(6.2.2а) (6.2.2б)
(6.2.2б)


