
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение, преломление, поглощение и пропускание монохроматического излучения – количественные соотно-шенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2.1. Количественные характеристики прохождения монохроматиче-ского луча через пластину из оптического материала 2.2. Отражение на границе раздела двух сред 2.2.1. Отражение на границе раздела двух прозрачных сред 2.2.2. Отражение на границе сильно поглощающего материала 2.3. Поглощение излучения в материале. Закон Ламберта-Бугера Оптика материала в диапазоне прозрачности и его фундаментальные спектры поглощения как взаимосвя-занные классы физических явлений: ранние подходы 3.1. Феноменология 3.2. Соотношения Крамерса-Кронига 3.3. Описание частотной зависимости оптических постоянных в явном виде: начало истории 3.3.1. Формула Зелльмейера 3.3.2. Контур линии поглощения в теории Лоренца Классическая теория дисперсии и ее аналитические модели дисперсии оптических постоянных кристаллов 4.1. История классической теории дисперсии. Дисперсионные уравне-ния для комплексной диэлектрической проницаемости (аналитические модели Друде и Лоренц-Лорентца) 4.1.1. Аналитическая модель дисперсии диэлектрической проницае-мости в приближении отсутствия локального поля (модель Друде) 4.1.2. Аналитическая модель дисперсии диэлектрической проницае-мости с поправкой на локальное поле (модель Лоренц-Лорентца) 4.1.3. Представления о рефракции 4.2. Классическое уравнение дисперсии комплексной диэлектрической проницаемости в современной науке. Модификация аналитической модели Друде 4.2.1. Некоторые формальные преобразования 4.2.2. Современное истолкование физического смысла параметров классической аналитической модели Друде Влияние специфики структуры стекол на их оптические свойства 5.1. Неупорядоченность структуры как основополагающая особенность природы стеклообразного состояния 5.2. Следствия неупорядоченности структуры для оптических свойств 5.3. Дисперсионное уравнение для комплексной диэлектрической проницаемости стеклообразных веществ (аналитическая модель свертки) Методы количественной обработки экспериментальных оптико-спектроскопических данных 6.1. Методы двух углов и двух поляризаций 6.2. Метод Крамерса-Кронига 6.3. Метод дисперсионного анализа Оптические характеристики, используемые в фотонике и технологии оптических материалов для описания свойств стекол в диапазоне их прозрачности 7.1. Основные оптические характеристики 7.2. Диаграмма Аббе 7.3. Хроматические аберрации и их устранение 7.4. Частные дисперсии и относительные частные дисперсии 7.5. Правило Аббе. Нормальная прямая и "особые" стекла 7.6. Нормируемые и справочные характеристики качества оптического стекла Литература Введение Начиная знакомство с данным разделом дисциплины "Оптическое материаловедение", студентам нужно иметь в виду, что этот раздел предполагает наличие у них некоторого базового объема знаний по смежным естественнонаучным дисциплинам (таким, как, например, «Физика твердого тела»). Необходимость таких исходных базовых знаний обусловлена тем, что при изложении всех вопросов от самых истоков непосредственно в данном разделе дисциплины объем этого раздела превысил бы все разумные рамки. При этом следует также учитывать, что любые названия конкретных дисциплин являются достаточно условными. В природе не существует жестких разграничительных линий между различными классами явлений. Поэтому, например, в средние века, когда весь имеющийся объем знаний о естественных науках еще мог быть охвачен и проанализирован мозгом одного человека, не возникало и необходимости как-то разграничивать эти науки друг от друга, и все они обозначались единым термином – натурфилософия. По мере развития естественных наук исследователи оказались вынужденными проводить какие-то разграничительные линии, чтобы структурировать все возрастающий объем знаний и получить возможность специализироваться в тех или иных направлениях. Естественно, эти разграничительные линии и, соответственно, названия конкретных дисциплин менялись и продолжают меняться с течением времени. Например, первое издание всеобъемлющей монографии Роберта Вуда, вышедшее в 1909 г., называлось «Физическая оптика»: в то время понятие «Физическая оптика» включало в себя почти все, что к тому времени было известно существенного обо всем классе оптических явлений (включая вопросы, выделившиеся позднее в направление «Спектроскопия»). Вышедшая в 1967 г. монография Макса Гарбуни «Оптическая физика» (в русском переводе – «Физика оптических явлений» [1]) снова освещает, несмотря на различие названий, тот же круг общих вопросов, что и монография Роберта Вуда, отражая при этом уже значительно более поздний этап развития данной области науки и включая ряд новых аспектов. Современное же содержание термина «Оптическая физика» (как можно видеть, например, по дисциплине, обозначаемой этим термином в действующей учебной программе естественнонаучного цикла) стало существенно более узким по части изложения общих вопросов, но зато затрагивает многие новые направления, еще только появившиеся или даже просто не существовавшие во времена Макса Гарбуни. Ввиду такой условности границ между различными смежными дисциплинами некоторые исходные моменты излагаемых ниже вопросов (включая математические соотношения) неизбежно перекликаются с теми, которые представлены и в других дисциплинах (например, в тех же дисциплинах естественнонаучного цикла «Физика твердого тела» и «Оптическая физика»). Присутствие ряда таких общих исходных моментов в данном разделе необходимо ради сохранения логической последовательности изложения, так как здесь эти моменты и соотношения развиваются далее и детализируются до уровней, не достигаемых в других дисциплинах. Сравнивая аналогичные исходные уравнения в различных дисциплинах, следует иметь в виду, что набор мировых констант, участвующих в том или ином уравнении, и положение в нем множителя 2 p могут различаться в зависимости от выбора системы единиц. В данном разделе все уравнения приводятся для системы единиц CGSE, так как в системе СИ они были бы более громоздкими из-за необходимости введения дополнительных констант (прежде всего диэлектрической проницаемости вакуума, являющейся в системе СИ размерной величиной в отличие от системы CGSE, где она безразмерна и равна единице). Известно, что в качестве оптических материалов могут использоваться не только твердые тела, но и вещества в других агрегатных состояниях (например, жидкие и газообразные активные среды для некоторых типов лазеров). Однако в подавляющем большинстве случаев оптические материалы являются твердотельными, то есть по своей физической природе они относятся либо к кристаллам, либо к стеклам. Поэтому данный раздел дисциплины посвящен, прежде всего, именно этим классам оптических материалов. Общая схема взаимосвязей между различными группами оптических материалов приведена на рис. 1. Все оптические материалы для удобства последующего рассмотрения можно условно разделить по их практическому применению на две больших группы - пассивные и активные материалы (см. рис. 1). Пассивные оптические материалы служат для передачи световых потоков, несущих энергию излучения или оптическое изображение, и для формирования этого изображения. Активные оптические материалы служат дляуправления световыми потоками и генерации этих потоков. Исторически первые оптические материалы были именно пассивными материалами, а активные материалы возникли позднее. Они разрабатывались, используя имевшиеся пассивные оптические материалы как исходные матрицы для последующей модификации путем введения активаторов (то есть добавок определенных веществ) или направленного создания дефектов, которые придают матрице дополнительные свойства. Поэтому для понимания всей совокупности оптических свойств даже самых сложных современных активных материалов совершенно необходимы глубокие знания в области механизмов формирования оптических свойств пассивных материалов. Основополагающим требованием к пассивным оптическим материалам является оптическая однородность, то есть отсутствие заметных изменений волнового фронта при прохождении через слой материала в произвольно выбранном направлении. Вопрос об оптической однородности ставится принципиально различным образом для кристаллических и стеклообразных материалов. Для кристаллов наличие правильной решетки, обладающей свойством трансляционной симметрии, предопределяет, как известно, неизбежную анизотропию большинства или даже всех их свойств (более подробно данный вопрос уже рассматривался в предшествующем разделе данной дисциплины и затрагивался также в дисциплине естественнонаучного цикла «Физика твердого тела»). Изотропность оптических свойств и соответственно оптическая однородность свойственны лишь кристаллам кубической сингонии, для которых скорости распространения световой волны по трем осям решетки совпадают (тогда как некоторые другие их свойства – например, механические – все же обладают анизотропией). Для стекол, лишенных технологических дефектов, полная изотропность всех их свойств и соответственно оптическая однородность являются, напротив, их характерными отличительными чертами. Это обусловливается такой принципиальной физической особенностью стеклообразного состояния вещества как случайная неупорядоченность его структуры (этот вопрос более подробно затрагивается ниже в параграфе 5.1, а также рассматривается в последующем разделе данной дисциплины). К сожалению, в русскоязычной научной и педагогической литературе отсутствуют какие-либо издания, охватывающие достаточно большую часть тематики данного раздела дисциплины. Известные переводные монографии [1-3] уже не соответствуют современному состоянию науки и к тому же освещают лишь общие вопросы, не затрагивая расчетных методов и задач практического применения оптических материалов. То же самое относится и к хорошо известному учебнику [4]. Поэтому значительная часть необходимого материала оказывается рассеянной по узкоспециализированным монографиям (например, [5-7]) и оригинальным журнальным публикациям, а некоторые вопросы вообще не освещены в русскоязычной литературе. В англоязычной литературе превалируют те же тенденции – с тем исключением, что тематика данного раздела достаточно широко излагается как целое в монографии [8]. Однако эта монография имеется лишь в двух крупнейших научных библиотеках Петербурга и Москвы и поэтому мало доступна студентам. Данное учебное пособие призвано в какой-то мере возместить эти пробелы в имеющейся литературе.
Общая схема взаимосвязей между различными группами оптических материалов. Основные понятия физики оптических явлений в твердых телах Общие соотношения На макроскопическом уровне поведение материала под воздействием электрического поля световой волны определенной частоты описывается в линейном приближении с помощью уравнений Максвелла (см., например, [2]). Уравне́ния Ма́ксвелла (1864 г.) - основные уравнения классической электродинамики, описывающие эволюцию электромагнитного поля и его взаимодействие с зарядами и токами. В данном пособии они подробно не рассматриваются. Чтобы дать общее представление об уравнениях Максвелла, ниже приводится их вид в системе единиц CGSE:
Здесь: · ρ — плотность электрического заряда (в единицах СИ — Кл/м³); · j — плотность электрического тока (в единицах СИ — А/м²); · λ — удельная проводимость или, что то же, электропроводность (в единицах СИ — м/Ом); · E — напряжённость электрического поля (в единицах СИ — В/м); · H — напряжённость магнитного поля (в единицах СИ — А/м); · D — электрическая индукция (в единицах СИ — Кл/м²); · B — магнитная индукция (в единицах СИ — Тл = Вб/м²= кг·с-2·А-1); · rot — дифференциальный оператор ротора; · div — дифференциальный оператор дивергенции. Магнитная и электрическая постоянные вакуума обозначаются через ε0 и μ0. Поэтому для вакуума электрическая и магнитная индукция может быть записана (без учета очень малых квантовых эффектов) в виде
Уравнения Максвелла для вакуума без электрических зарядов и токов имеют вид:
Эта система дифференциальных уравнений имеет простое решение — гармоническая, плоская волна. Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу, и находятся в фазе. Волна распространяется со скоростью
где c - скорость света в вакууме. Общепринятые значения скорости света, электрической и магнитной постоянных в системе СИ приведены в таблице.
Для понимания дальнейшего изложения данной дисциплины достаточно знать, что, согласно решениям уравнений Максвелла, а) отклик материала на воздействие электрического поля световой волны полностью определяется его диэлектрической проницаемостью при этой частоте; б) диэлектрическая проницаемость материала с любой конечной (не равной нулю) электрической проводимостью (то есть любого материала, кроме вакуума) является комплексной величиной. Таким образом, используя широко распространенное в математике обозначение комплексной величины с помощью значка ˆ над ее символом, можно написать: Поскольку диэлектрическая проницаемость – это всегда квадрат показателя преломления, то показатель преломления также оказывается комплексной величиной
Соответственно e¢ = n 2 - k 2 (1.1.2а) и e¢¢ = 2 n´k. (1.1.2б) Рассмотрим теперь в общих чертах, что происходит в материале на микроуровне при воздействии на него электрической составляющей электромагнитного поля световой волны. Под воздействием приложенного электрического поля световой волны имеющиеся в нем электрические заряды (электроны, ионы и атомы, несущие какие-либо эффективные заряды) смещаются в направлении соответствующих полюсов. Это явление называется поляризацией материала. В результате в нем возникают наведенные диполи (которые добавляются к постоянным диполям, если таковые имелись в материале). Количественной мерой поляризации материала служит вектор поляризации (или, кратко, просто поляризация) Таким образом, действительная и мнимая части комплексной диэлектрической проницаемости (равно как и показателя преломления), которые определяют преломляющие и абсорбционные свойства материала соответственно, не являются независимыми: существует глубокая внутренняя взаимосвязь этих на первый взгляд различных свойств. Эта взаимосвязь подробно рассматривается ниже в подразделах 3-5. Во всех дисциплинах, относящихся к области физики оптических явлений, принято обозначать взаимосвязанные пары величин e¢ и e¢¢ и/или n и k собирательным термином «оптические постоянные». Именно такой смысл термина «оптические постоянные» и используется в данном учебно-методическом пособии.[3] В простейшем случае равенства внешнего (приложенного) электрического поля E и внутреннего электрического поля в материале E int[4] значение вектора поляризации
где N - число заряженных частиц (электронов, атомов или ионов) в единице объема вещества. Комплексный коэффициент пропорциональности Как же связать эту микроскопическую характеристику с вышеописанными характеристиками макромира? Из электростатики известно, что
Приравнивая это выражение и вышеприведенное выражение (3) для P, получаем, что в приближении равенства внешнего и внутреннего электрического поля комплексная диэлектрическая проницаемость выражается через поляризуемость соотношением
До сих пор рассмотрение ограничивалось случаем постоянной частоты световой волны (т. е. случаем монохроматического излучения). Однако оптические постоянные всегда являются, как известно, функциями частоты, что не рассматривается в рамках решений уравнений Максвелла (они являются слишком общими для такого рассмотрения). Поэтому, строго говоря, вышеприведенные выражения для
и
Здесь w - текущая круговая частота, являющаяся аргументом соответствующих функций. Она связана с длиной волны l соотношением w = 2p c/l, где c - скорость света. Наряду с круговой частотой используются и другие характеристики частоты: · линейная частота n (здесь n - греческая буква «ню»; не путать с латинской v!), характеризующая число периодов волны в секунду (размерность – Гц), · n = c/l = w/ 2p; · волновое число
Линейная частота используется, как правило, для волн радиодиапазона, а волновое число – для волн инфракрасного (ИК) диапазона. Для областей очень высоких частот излучение принято характеризовать также энергией кванта E (в эВ):
где h – постоянная Планка, или, при выражении длины волны в мкм,
Прежде чем переходить к анализу частотной зависимости оптических постоянных, необходимо напомнить вкратце физическую природу поглощения оптического излучения в различных спектральных диапазонах, а также количественные соотношения, описывающие изменения характеристик светового потока при прохождении через слой оптического материала.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.151 (0.03 с.) |


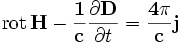








 ,
,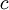


 .
. , в которой действительная часть n – это знакомый всем из школьного курса физики показатель
, в которой действительная часть n – это знакомый всем из школьного курса физики показатель  . (1.1.1)
. (1.1.1) - суммарный наведенный дипольный момент [2] единицы объема. Наличие не равного нулю поглощения энергии световой волны в материале вызывает отставание вектора поляризации
- суммарный наведенный дипольный момент [2] единицы объема. Наличие не равного нулю поглощения энергии световой волны в материале вызывает отставание вектора поляризации  по фазе от внешнего электрического поля этой волны Е, что и приводит к необходимости описания вектора поляризации и диэлектрической проницаемости (а, следовательно, и показателя преломления) как комплексных величин.
по фазе от внешнего электрического поля этой волны Е, что и приводит к необходимости описания вектора поляризации и диэлектрической проницаемости (а, следовательно, и показателя преломления) как комплексных величин. определяется соотношением
определяется соотношением , (1.1.3)
, (1.1.3) между приложенным полем и вкладом в значение вектора поляризации называется поляризуемостью соответствующей частицы вещества. Таким образом, поляризуемость служит микроскопической характеристикой поляризации.
между приложенным полем и вкладом в значение вектора поляризации называется поляризуемостью соответствующей частицы вещества. Таким образом, поляризуемость служит микроскопической характеристикой поляризации. . (1.1.4)
. (1.1.4) . (1.1.5)
. (1.1.5) и
и  следует переписать в виде
следует переписать в виде (1.1.6)
(1.1.6) . (1.1.7)
. (1.1.7)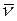 (его размерность – см-1):
(его размерность – см-1):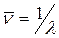 .
. ,
,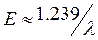 .
.


