
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закономерности излучения абсолютно черного телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Закон Стефана - Больцмана. Полная (по всему спектру) излучательная способность абсолютного черного тела прямо пропорциональна четвертой степени его абсолютной (термодинамической) температуре Т: εT = где σ =5,67.10─8 Вт/м2К4 постоянная Стефана – Больцмана. εT численно равна площади фигуры, ограниченной кривой ελ,T. и горизонтальной осью λ. 2. Закон смещения Вина (1893г). Длина волны (λмакс), на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна его абсолютной (термодинамической) температуре Т. λмакс=b /T, где b = 2,9.10-3 м К постоянная Вина. Этим объясняется изменение цвета физических тел при изменении их температуры. Например, для металлических предметов при комнатных или чуть выше температур, максимум их теплового излучения находится в инфракрасной части спектра, поэтому мы это излучение не видим. Когда мы повышаем температуру металла, максимум его теплового излучения перемещается в сторону коротких волн и мы видим его как свечение раскаленного металла. У Солнца, при температуре Т≈58000К, максимум теплового излучения приходится в видимый часть спектра (λмакс ≈500 нм),который, отчасти, совпадает с максимумом чувствительности нашего глаза. Значения λмакс и ν макс не связаны формулой с=λ·ν, т.к. максимумы εν,Τ и ελ,Т расположены в разных частях спектра. Законы 1 и 2 выводились, опираясь на закономерности классической термо- и электродинамики.
3. Формула Рэлея - Джинса Для малых ν и больших λ и Τ εν,Τ= но при больших ν или когда hν>>kT она резко расходится с экспериментальной кривой.
4. Формула Вина (закон излучения Вина) Для больших ν и малых λ и(hν>>kT) εν,Τ =cν3f(ν/T) или ελ,Τ= Для объяснения распределения энергии в спектре абсолютно черного тела немецкий физик М.Планк выдвигал чрезвычайно смелую гипотезу, которая, в дальнейшем, блестяще подтвердилась и коренным образом изменила развитию физики, и не только физики. Для этого ему пришлось отказаться от установившегося в физике представления об электромагнитном излучении как о непрерывной электромагнитной волне, которая может иметь любую частоту и в соответствии с этим переносить любую энергию. Всякое тело состоит из громадного количества атомов; каждый из них по своим свойствам излучать электромагнитные волны подобен миниатюрному вибратору, который колеблется со многими частотами и излучает энергию соответствующих частот. Поэтому считалось, что тела излучают электромагнитные волны всевозможных частот, а их излучение непрерывно. Согласно гипотезе Планка, энергия атома – вибратора может изменяться лишь определенными отдельными порциями (квантами)[17], кратными некоторой энергии ε, т.е может принимать только значения ε, 2ε, 3ε,…, nε. Величина элементарной порции энергии называется квантом энергии и определяется как: ε = hν = hc/λ где ν и λ – частота и длина волны колебания атома, h – универсальная постоянная Планка (h=6,625.10-34 Дж . с). По гипотезе Планка атомы не только имеют дискретные значения энергии, но излучают и поглощают электромагнитные волны дискретными порциями, кратными величины hν. На основе представлений о квантовом характере теплового излучения Планк получил математическое выражение для ελ,T, которое полностью соответствовало экспериментальным данным.
В атомной физике используется также другое значение постоянной Планка ħ=h/2π, при этом элементарная порция энергии кванта ε = ħω, где ω – круговая частота (ħ=1,055·10─34Дж·с). Зная σ и b можно вычислить h, k, c, и наоборот, h, k, c можно выражать через σ и b. Например, σ=
Фотоэффект Фотоэлектрическим эффектом (фотоэффектом) называется освобождение (полное или частичное) электронов от связей с атомами и молекулами вещества под воздействием света (видимого, инфракрасного и ультрафиолетового). Для твердых и жидких тел различается внешний и внутренний фотоэффект. Если под воздействием света электроны выходят за пределы освещаемого вещества (полное освобождение), то фотоэффект называется внешним (открыт в 1887г. Г.Герцем). Если же электроны теряют связь только со «своими» атомами и молекулами, но остаются внутри освещаемого вещества (полупроводники и в меньшей мере диэлектрики) в качестве «свободных электронов» (частичное освобождение), увеличивая тем самым электропроводимость вещества, то фотоэффект называется внутренним. В газах фотоэффект состоит в явлении фотоионизации – вырывании электрона из атомов и молекул газа под действием света. Электроны, вылетающие с поверхности тела пи внешнем фотоэффекте, называются фотоэлектронами. Фотоэлектроны, ускоренные электрическим полем между катодом и анодом, создают фотоэлектрический ток (фототок). На рисунке приведена зависимость фототока I, от напряжения U между катодом и анодом (вольт - амперная характеристика фотоэффекта). Из этой зависимости следует, что по мере увеличения U фототок постепенно возрастает, т. е. все большое число фотоэлектронов достигает анода. Максимальное значения тока Iнас. - фототока насыщения – определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода.
Основные закономерности внешнего фотоэффекта: 1. При фиксированной частоте падающего света сила фототока насыщения Iнас. Прямо пропорциональная падающему интенсивности света Е или световому потоку (закон Столетова): Iнас=γЕ, где γ – коэффициент чувствительности облучаемой поверхности. Он зависит от природы и состояния поверхности, а также от λ. 2. Независимо от интенсивности света фотоэффект начинается только при определенной (для данного вещества) минимальной частоте света, называемой красной границей фотоэффекта (ν0). Фотоэффект имеет место когда ν>ν или λ<λ (λ0=с/ν0). 3. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с ростом частоты света и не зависит от его интенсивности Внешний фотоэффект безинерционен: фототок возникает через 10 -9 с после освещения катода. Находящиеся внутри металла свободные электроны не могут выйти из металла, так как кулоновские силы положительных ядер притягивают их обратно. Чтобы электроны вырвались наружу, надо совершить работу, для чего у тепловых электронов не хватает энергии. Когда свет падает на металл, то энергия света передается электрону, который уже может совершить работу выхода из вещества. Весь вопрос был в том – как свет передает свою энергию электрону. Все попытки объяснить этот процесс, исходя из волновой природы света, не венчались успехом. Тогда Эйнштейн, используя идею Планка о квантах электромагнитного излучения, представил этот процесс передачи энергии света электрону как взаимодействие световых квантов (фотонов [18]) с электроном. Каждый фотон взаимодействует только с одним электроном и передает ему всю свою энергия, равную hν. Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии meυ2макс /2. По закону сохранения энергии: hν = А + meυ2макс /2 (Уравнение Эйнштейна для внешнего фотоэффекта). Гипотеза Эйнштейна, которая в дальнейшем блестяще подтвердилась, полностью объяснила все экспериментальные закономерности фотоэффекта. Фототок исчезает тогда, когда кинетическая энергия фотоэлектрона meυ2макс /2 ровняется работе, которую надо совершить чтобы преодолеть задерживающее электрическое поле eUз. Красная граница фотоэффекта можно найти из hν0=A → ν0=A/h. Так же λ0=c/ν0=hc/A. При внутреннем фотоэффекте проводимость полупроводника (диэлектрика) резко увеличивается при их освещении. Существует также многофотонный (нелинейный) фотоэффект, при котором электрон получает энергию от N фотонов (при очень большой интенсивности света или лазера). В этом случае уравнение Эйнштейна принимает вид: Nhν=A+mυ2/2, а красная граница длин волн увеличивается. В настоящее время в различных областях науки и техники широко используются фотоэлементы – приемники излучения, работающие на основе фотоэффекта преобразующие энергию излучения в электрическую. Квантовая теория электромагнитных волн и эйнштейновское объяснение фотоэффекта окончательно подтвердили квантовую сущность света. Получилась странная ситуация с точки зрения классической физики, которая всегда четко разграничивала объекты, имеющие волновую природу (например, свет и звук), и объекты, имеющие дискретную корпускулярную структуру (например, система материальных точек). Свет в некоторых явлениях (интерференция, дифракция, дисперсия и др.) себя ведет как волна, а в некоторых явления (излучение черного тела, фотоэффект и др.) – как частица – фотон. Одним из наиболее значительных достижений современной физики заключается в том, что она не противопоставляет друг другу волновые и квантовые свойства света. Двойственную природу света (корпускулярно - волновой дуализм света) объясняется тем, что в некоторых явлениях более четко выражается волновые свойства света, а в некоторых – корпускулярные. Чем больше длины волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые свойства света и, наоборот, чем меньше длина волны, тем больше энергия и импульс фотона и тем труднее обнаруживаются волновые свойства света. Одна из попыток объяснить корпускулярно-волновой дуализм сводиться к понятиям волновых пакетов. Дело в том, что, излучение никогда не может быть охарактеризовано единственной точно определенной частотой. О частоте волны можно говорить в том случае, когда эта волна равномерно распределена во всем пространстве. Это означает, что волна с единственной частотой должна иметь бесконечную протяженность. Однако все генераторы электромагнитных волн, будь то антенны или атомы, изучают лишь в течение конечных отрезков времени. Следовательно, волны излучения никогда не имеют бесконечной протяженности и не могут поэтому характеризоваться единственной частотой. Существующее в действительности излучение всегда состоит из набора (суперпозиции) волн с разными частотами. Если эти частоты заключены в узкой области около центральной частоты, то интерференция соответствующих волн оказывается конструктивной в одной области пространства и деструктивной во всем остальном пространстве. Результат такой суперпозиции волн приводит к тому, что колебания локализируются в ограниченном пространстве. Такая локализованная группа колебаний называется волновым пакетом. Волновой пакет электромагнитного излучения (т.е. фотон) распространяется как целое со скоростью света.
Волновой пакет, показанный в рисунке, состоит только из 6 колебаниями; в случае светового фотона, подобного только что описанному, волновой пакет имеет примерно 10 5−106 колебаний. Пакет, составленный из столь большого числа колебаний, сохраняет многие из своих волновых характеристик. Но вместе с тем он будет дискретным образованием, так что будет взаимодействовать, например, при комптоновском рассеянии или в фотоэлектрическом эффекте, с каждым электроном в отдельности. Свет не волна и не частица, а и волна, и частица одновременно! Строение вещества § 3.1. Модели атома Резерфорда Ученых всегда интересовал вопрос – как устроена материя? Из чего состоит окружающее нас вещество? Еще древние греки предполагали, что вещественный мир состоит из мельчайших частиц, называемых атомами. Атомами (от древнегреческого слова «неделимое») называли самые маленькие частицы вещества, которые еще сохраняют свойства данного вещества. Следует отметить, что в некоторых книгах под атомами, не без основания, подразумевают и молекулы, так как последние тоже удовлетворяют такому определению атома. Ведь разделив молекулу воды на атомы, мы получаем уже не воду, а отдельные атомы водорода и кислорода. Но, тем не менее, пока общепринято молекулами обозначать совокупность различных атомов. Это, по сути, философское определение осталось неизменным вплоть до конца XIX века. К тому периоду химические науки достигли больших успехов. Периодическая система химических элементов Д.И.Менделеева (1869г.) позволила правильно расположить по клеточкам известные в то время 64 элемента и уточнить многие их характеристики (например, атомный вес некоторых из них). Более того, она предсказала существование новых, еще не открытых элементов и их основные свойства (количество открытых химических элементов перевалило за сотню: недавно российскими учеными был открыт, пока не имеющий названия, элемент №118). С открытием электрона английским физиком Дж.Дж.Томсоном (1897г.), серьезно встал вопрос о внутренней структуре атома. Сам Дж.Дж.Томсон попытался на основе накопленных экспериментальных данных создать модель атома. Факты, которые лежат в основе его модели таковы: линейные размеры атомов с различными массами приблизительно равны 10 -10 м, внутри них находятся отрицательно заряженные электроны, а сам атом электрически нейтрален. По этому, согласно модели Томсона, атом представляет собой непрерывно заряженный положительным зарядом шар с определенной массой и радиусом ~10-10 м, внутри которого около своих положений равновесия колеблются электроны, суммарный отрицательный заряд которых равен положительному заряду шара. Но эксперименты Э.Резерфорда с рассеянием α-частиц (об α-частицах см. «радиоактивность»), проходящих через вещество, опровергли эту модель. Знаменитый опыт Резерфорда схематично показан на рисунке, где поток α–частиц двигаясь в Исходя из результатов своих опытов Резерфорд 1911г. предложил ядерную (планетарную) модель строения атома [19]. По этой модели, весь положительный заряд и почти вся масса (>99,94%) атома сосредоточены в атомном ядре, размер которого ничтожно мал (порядка 10-15–10-14 м ) по сравнению с размером атома (10-10 м). Вокруг ядра по замкнутым орбитам, как планеты вокруг Солнца, движутся электроны, образуя электронную оболочку атома. Заряд ядра, величина которого совпадает с порядковым номером химического элемента, равен по абсолютному значению суммарному заряду электронов. Таким образом, атом в целом является чрезвычайно «ажурным» микрообразованием: совокупностью небольшого числа очень малых частиц вещества (ядра и электронов), расположенных в сравнительно большом объеме.
Постулаты Бора Внешне привлекательная модель Резерфорда имела внутренние противоречия: электрон, вращаясь вокруг ядра (т.е. двигаясь с ускорением), по всем законам классической электродинамики, должен испускать электромагнитное излучение, терять свою энергию, и постепенно приближаясь к ядру, в конце концов, упасть на него (расчеты указывают время падения ~10-8 с). Другое затруднение в рамках классической физики создавал объяснение линейчатых спектров водорода и других химических элементов. Компромиссное решение для атомов водорода и водородоподобных атомов (He+, Li2+, Be3+ и тому подобных) предложил 1913г. датский физик Н. Бор, выдвинув свои постулаты. Постулаты Бора. Электроны могут двигаться в атоме не по любым орбитам, а только по стационарным орбитам вполне определенного радиуса. Движение электронов по стационарным орбитам НЕ сопровождается излучением (поглощением) энергии. 2. Переход электрона с одной стационарной орбиты на другую сопровождается излучением (или поглощением) одной порции (кванта) энергии. Энергия этого кванта электромагнитного излучения равна разности энергий стационарных состояний атома до (W1) и после (W2) излучения (поглощения) и выражается через: где h = 6,63 . 10 -34 Дж . с постоянная Планка,
Таким образом, частота электромагнитных волн, излучаемых атомом, определяется не частотой вращения электронов в атоме, а разностью энергии стационарных состояний атома. Эта разность энергии стационарных состояний для каждого атома, иона имеет строго определенные значения, которыми объясняется постоянный, индивидуальный набор спектральных линий данного атома или иона. Обобщая постулаты Бора Атом устойчив только в состояниях, соответствующих дискретным значениям энергии (W 1, W 2, W 3,…); переход атома из одного устойчивого состояния в другое сопровождается излучением или поглощением кванта энергии, определяемого условием частот.
Применение постулатов Бора с законами классической физики позволяет определить радиусы стационарных орбит атома водорода. Кулоновская сила Отсюда При n=1 R1≈0,053нм≈0,53 . 10-10м. В атомной физике это значение (Боровский радиус) используется как единицу измерения длины. Кинетическая и потенциальная энергия атома водорода: Wкин = Wпот = Общая энергия W =Wкин +Wпот = Где использовано выражение для r и ħ=h/2π. W <0 т.к. уровня отсчета потенциальной энергии выбран так, что W →0 при r→∞. W1=−13,56эв, это и есть энергия ионизации водорода. Из постулата Бора hν=Wk −Wn частота излучения при переходе n→k.
где R= Квантовая теория Бора, количественно хорошо объясняя строение атома водорода и водородоподобных элементов, неприменима для многоэлектронных атомов. Тем не менее, она дает возможность качественно (и притом весьма наглядно) объяснить общие черты строения многоэлектронных атомов и их спектров, в частности дает возможность обосновать закономерности расположения химических элементов в периодической системе Менделеева. § 3.3. Правила отбора Паули, квантовые числа и таблица Менделеева В квантовой механике строение многоэлектронных атомов объясняется при помощи четырех квантовых чисел, которые однозначно характеризуют движение электрона вокруг ядра. 1. Главное квантовое число n определяет энергетические уровни атома, общие для группы электронов и принимает только целочисленные значения от 1 до ∞. Электроны с одинаковым n образуют электронные оболочки с буквенными обозначениями: n=1(K), 2(L), 3(M), 4(N), 5(O), 6(P), 7(Q),… Строго говоря, квантовые числа связаны с волновыми свойствами атомных электронов, но в целях наглядности квантовым числам обычно приписывают также геометрический смысл. В данном случае, главное квантовое число определяет размер орбиты (ее радиус в случае круговой или большую полуось в случае эллиптических орбит). Как мы убедились, у водорода с ростом n увеличивается размер по закону rn~n2. n=1 соответствует основному, невозбужденному состоянию атома водорода, все остальные с n=2,3,…, - возбужденному. 2. Орбитальное (побочное) квантовое число ℓ определяет энергетические подуровни атома и, при заданном n, принимает целочисленные значения от 1 до n-1 (всего n значения). Электроны с одинаковыми ℓ образуют электронные подоболочки с буквенными обозначениями: ℓ= 0(s), 1(p), 2(d), 3(f), 4(g), 5(h),…, n-1 (всего n значений).
mℓ принимает целочисленные значения от _ ℓ до +ℓ (всего 2 ℓ+ 1 значений): mℓ = 0, ±1, ±2, …±ℓ. 4. Спиновое квантовое число ms (иногда обозначают s) характеризует ориентацию (знак) спина электрона и может принимать только два значения: ms. =±1/2 (что соответствует противоположно направленным спинам электронов). Спин (как заряд) определяет собственный (внутренний) момент импульса (количество движения) частицы, обусловленный ее квантовой природой. Распределение электронов в атоме подчиняется п ринципу Паули (1925) (принцип исключения). · В одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел Руководствуясь этим принципом, предлагается самостоятельно вывести формулу для максимального числа электронов в оболочке Z(n)= · Принцип минимума энергии – электроны заполняют энергетические уровни атома так, чтоб их распределение в атоме соответствовало минимуму энергии атома. Каждый последующий уровень электроны заселяют тогда, когда полностью заполнены предыдущие уровни. Однако это условие выполняется для химических элементов до №=19 (Калий), после чего минимум энергии распределения электронов в атоме достигается, если электроны, не заполняя какие-то нижние подоболочки, занимают более высокие уровни. Это происходит из-за того, что с увеличением количества электронов, увеличиваются кулоновские взаимодействия между электронами. Поэтому и в оптическом, и в химическом отношениях атом К схож с атомами Li и Na, которые также имеют внешний валентный электрон в s-состоянии. Аналогично атом Ca схож атомам Be и Mg. В нижестоящей таблице представлены обозначения оболочек и подоболочек, а также распределение электронов по оболочкам и подоболочкам в атоме.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.011 с.) |

 ελ,Tdλ=σT4,
ελ,Tdλ=σT4, (~ 1/λ2),
(~ 1/λ2),
 или
или 
 ,
, 
 Из ВАХ фотоэффекта видно, что при U=0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью υ, а значит, отличной от нуля кинетической энергией meυ2макс /2 и поэтому могут достигнуть анода без (вопреки) внешнего поля. Фототок исчезает при некотором задерживающем напряжении Uз, когда ни один из электронов, даже обладающий при вылете из катода максимальной скоростью υмакс, не может преодолеть задерживающего поля и достигнуть анода.
Из ВАХ фотоэффекта видно, что при U=0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью υ, а значит, отличной от нуля кинетической энергией meυ2макс /2 и поэтому могут достигнуть анода без (вопреки) внешнего поля. Фототок исчезает при некотором задерживающем напряжении Uз, когда ни один из электронов, даже обладающий при вылете из катода максимальной скоростью υмакс, не может преодолеть задерживающего поля и достигнуть анода. Область частот, соответствующая световому фотону, чрезвычайно узка. Возьмем, например, фотон желтого света с центральной частотой 5.1014с-1. При излучении такого фотона атомом область частот вокруг центральной частоты соответствует всего лишь Δν/ν ≈ 2.10-6, что отвечает диапазону длин волн 0,001нм. Это означает, что ни одна из спектральных линий не является абсолютно резкой. Все они всегда имеют некоторую естественную ширину.
Область частот, соответствующая световому фотону, чрезвычайно узка. Возьмем, например, фотон желтого света с центральной частотой 5.1014с-1. При излучении такого фотона атомом область частот вокруг центральной частоты соответствует всего лишь Δν/ν ≈ 2.10-6, что отвечает диапазону длин волн 0,001нм. Это означает, что ни одна из спектральных линий не является абсолютно резкой. Все они всегда имеют некоторую естественную ширину. вакууме и проходя сквозь золотую фольгу (толщиной около 1 мкм), падал на люминесцирующий экран. Удар каждой α–частицы об экран вызывал кратковременную вспышку – сцинтилляцию, наблюдаемую в микроскоп. Если модель Томсона соответствовала истине, α–частицы не могли прорваться через толщу фольги. Но результаты опытов Резерфорда оказались неожиданным: большинство α–частиц проходит сквозь фольгу без заметных отклонения от первоначального направления, некоторые частицы отклоняются на небольшой угол и лишь незначительная часть α–частиц претерпевает сильное отклонение. Поскольку легкие электроны при взаимодействиях с тяжелыми и очень быстрыми α–частицами не могут существенно изменить их движение, естественно предполагать, что отклонение α–частиц вызвано массивными атомными ядрами, которые, согласно результатам эксперимента, занимают очень небольшой объем в атоме.
вакууме и проходя сквозь золотую фольгу (толщиной около 1 мкм), падал на люминесцирующий экран. Удар каждой α–частицы об экран вызывал кратковременную вспышку – сцинтилляцию, наблюдаемую в микроскоп. Если модель Томсона соответствовала истине, α–частицы не могли прорваться через толщу фольги. Но результаты опытов Резерфорда оказались неожиданным: большинство α–частиц проходит сквозь фольгу без заметных отклонения от первоначального направления, некоторые частицы отклоняются на небольшой угол и лишь незначительная часть α–частиц претерпевает сильное отклонение. Поскольку легкие электроны при взаимодействиях с тяжелыми и очень быстрыми α–частицами не могут существенно изменить их движение, естественно предполагать, что отклонение α–частиц вызвано массивными атомными ядрами, которые, согласно результатам эксперимента, занимают очень небольшой объем в атоме. ,
,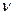 - частота электромагнитного излучения.
- частота электромагнитного излучения. При переходе электрона с одной стационарной орбиты на другую (ближнюю к ядру), излучается квант энергии, равный разности энергетических уровней атома до излучения и после него. Самопроизвольный переход электрона на более далекую орбиту, т.е. самопроизвольный переход атома на более высокий энергетический уровень, невозможен. Для осуществления такого перехода необходимо сообщить атому определенное количество энергии извне, т.е. возбудить атом.
При переходе электрона с одной стационарной орбиты на другую (ближнюю к ядру), излучается квант энергии, равный разности энергетических уровней атома до излучения и после него. Самопроизвольный переход электрона на более далекую орбиту, т.е. самопроизвольный переход атома на более высокий энергетический уровень, невозможен. Для осуществления такого перехода необходимо сообщить атому определенное количество энергии извне, т.е. возбудить атом. сообщает электрону центростремительное ускорение
сообщает электрону центростремительное ускорение  , удерживая его на орбите радиусом r. По второму закону Ньютона
, удерживая его на орбите радиусом r. По второму закону Ньютона  = m
= m 

 или r~n2 r1:r2:r3:r4:…=1:4:9:16:…
или r~n2 r1:r2:r3:r4:…=1:4:9:16:… ,
, , к ак потенциальная энергия между протоном (+е) и электроном (+е)
, к ак потенциальная энергия между протоном (+е) и электроном (+е) ,
, ,
, =1,0974.107м-1=3,29.1015с-1, (Rλ=Rν.c) постоянная Ридберга.
=1,0974.107м-1=3,29.1015с-1, (Rλ=Rν.c) постоянная Ридберга. Отсюда видно, что орбитальное квантовое число ℓ не может совпадать с главным квантовым числом n. Орбитальное квантовое число ℓ определяет значение орбитального момента импульса (механический орбитальный момент) электрона. Из квантовой теории вытекает, что момент импульсане может принимать произвольное значение и имеет дискретное значение по формуле: Lℓ=
Отсюда видно, что орбитальное квантовое число ℓ не может совпадать с главным квантовым числом n. Орбитальное квантовое число ℓ определяет значение орбитального момента импульса (механический орбитальный момент) электрона. Из квантовой теории вытекает, что момент импульсане может принимать произвольное значение и имеет дискретное значение по формуле: Lℓ=  . Орбитальное квантовое число ℓ определяет форму орбиты или ее эксцентриситет (расстояние между фокусами эллиптической орбиты). Иными словами, оно обусловливает ее вытянутость. Чем больше ℓ, тем больше вытянута эллиптическая орбита электрона (при ℓ= 0 или s мы имеем дело с круговым вращением электрона)[20]. А это означает, что если водород находится в невозбужденном состоянии, то электрон может вращаться только по круговой орбите. Другие формы орбит появляются, когда электрон поднимается на верхние, возбужденные уровни.
. Орбитальное квантовое число ℓ определяет форму орбиты или ее эксцентриситет (расстояние между фокусами эллиптической орбиты). Иными словами, оно обусловливает ее вытянутость. Чем больше ℓ, тем больше вытянута эллиптическая орбита электрона (при ℓ= 0 или s мы имеем дело с круговым вращением электрона)[20]. А это означает, что если водород находится в невозбужденном состоянии, то электрон может вращаться только по круговой орбите. Другие формы орбит появляются, когда электрон поднимается на верхние, возбужденные уровни. 3. Магнитное квантовое число mℓ определяет возможную пространственную ориентацию орбитального момента, проекция которого на заданное направление z (например на
3. Магнитное квантовое число mℓ определяет возможную пространственную ориентацию орбитального момента, проекция которого на заданное направление z (например на  внешнего магнитного поля) принимает ряд дискретных значении, кратных ħ (пространственное квантование): Lℓz=mℓ.ħ.
внешнего магнитного поля) принимает ряд дискретных значении, кратных ħ (пространственное квантование): Lℓz=mℓ.ħ. =2n2
=2n2


