
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновые свойства микрочастицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из универсального закона взаимосвязи массы и энергии вытекает, что энергия Е и масса mф фотона связаны соотношением: Е= mф. с2. Так как фотон обладает энергией E=hν, то его масса mф = Поставив это выражения массы в формулу импульса фотона, получаем, что импульс фотона Луи де Брайль в 1924 году пришел к выводу, что корпускулярно-волновой дуализм присущ не только излучению и световым фотонам, но и материальным частицам, то есть любая движущаяся частица вещества должна, как квант излучения – фотон, обладать и волновыми свойствами. Для длин волн микрочастиц, он предлагал выражение, аналогичное для фотона, т.е. любой частице, обладающей импульсом p=mυ, свойственна длина волны:
где Предсказанные де Бройлем волновые свойства частиц впоследствии были обнаружены экспериментально при наблюдении дифракции электронов и других частиц на кристаллах (опыты Дэвиссона-Джермера в 1927г.). Более того, было доказано, что волновые свойства частиц не являются свойствами их коллектива, а присущи каждой частице в отдельности. Проходя через металлическую фольгу, и пучок электронов, и идущие друг за другом отдельные электроны, показывают схожую дифракционную картину.
В связи с этим возникал вопрос; почему раньше в макромире не обнаружились волны де Бройля? Простые расчеты показывают, что, например, частице с m = 1мг и υ=1м/с, соответствует волна де Бройля с Рассчитав по формуле де Бройля длину волны
Существование волн де Бройля позволяет истолковать корпускулярно - волновой дуализм света в более широком смысле: двойственная природа присуща не только свету, но всем микрочастицам! Микрообъекты существенно (качественно) отличаются от привычных для нас объектов макромира. Для частиц или тел макромира такая двойственная природа невозможно представить. Частица макромира занимает ограниченную область пространства и движется по определенной траектории (или покоится); волна же распределена в пространстве непрерывно и ее энергия передается всем точкам пространства. Сочетая в себе свойства частицы и волны, микротела «не ведут себя ни как волны, ни как частицы …». Отличие микрочастицы от волны заключается в том, что она всегда обнаруживается как неделимое целое (никто никогда не наблюдал, например, полэлектрона). В то же время волну можно разделить на части (например, направив световую волну на полупрозрачное зеркало) и воспринимать затем каждую часть в отдельности. Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы ε и частотой ν волны де Бройля: ε =h ν. Это свидетельствует о том, что соотношение между энергией и частотой в этой формуле имеет характер универсального соотношения, справедливого как для фотонов, так и для любых других микрочастиц. Делались попытки корпускульярно-волновой дуализм объяснить моделями, где частицы рассматривались как «узкие» волновые пакеты, «составленные» из волн де Бройля. Это позволило, как бы отойти от двойственности свойств частиц. Такая гипотеза соответствовала локализации частицы в данный момент времени в определенной ограниченной области пространства. Тем более, что скорость распространения центра такого пакета (групповая скорость) оказалась равной скорости частиц. Однако подобное представление частицы в виде волнового пакета (группы волн де Бройля) оказалось несостоятельным из-за сильной дисперсии волн де Бройля. Т.к. скорость волн де Бройля зависит от длины волны, дисперсия приводила к «быстрому расплыванию» (примерно за 10-26с) волнового пакета или даже разделению его на несколько пакетов.
По словам академика Фока; «для атомного объекта (микрочастицы) существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна-частица. Всякое иное, более буквальное, понимание этого дуализма в виде какой-нибудь модели (классической) неправильно».
§3.8. Соотношение неопределенности Гейзенберга
Из корпускулярно – волнового дуализма следует, что применение к объектам микромира понятий классической механики (физики) не всегда правомерно и должно иметь некоторые ограничение. В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координаты и импульс. Микрочастицы из-за наличия у них волновых свойств существенно отличаются от классических частиц. Одно из основных различий заключается в том, что нельзя говорить о движении микрочастицы по определенной траектории и неправомерно говорить об одновременных точных значениях ее координаты и импульса: понятие «длина волны в данной точке» лишено физического смысла. Поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным. В.Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определенную координату (x, y, z), и определенную соответствующую проекцию импульса (px, py, pz), причем неопределенности этих величин удовлетворяют условиям Δx.Δpx ≥ h, Δy. Δpy ≥ h, Δz.Δpz ≥ h, т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h (h - постоянная Планка). Для микрочастиц не существуют состояний, в которых ее координаты и импульс одновременно имели бы точные значения.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.30.193 (0.012 с.) |

 .
. , отсюда
, отсюда  .
.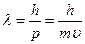 (формула де Бройля),
(формула де Бройля), - длина волны де Бройля, h =6,625.10-34 Дж.с – постоянная Планка.
- длина волны де Бройля, h =6,625.10-34 Дж.с – постоянная Планка.



