
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновые свойства микрочастиц. Гипотеза де Бройля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где А – постоянная амплитуда волны, k – волновой вектор (его направление совпадает с направлением распространения волны, а модуль равен 2π/λ). Согласно корпускулярно-волновому дуализму материи, ω = E/ħ и р = ħk. Учитывая эти соотношения и выражение (72), видим, что с движением частицы, имеющей определенные энергию и импульс, связывается волна вида называемая плоской волной де Бройля. Основные уравнения, связывающие корпускулярные свойства электромагнитного излучения (энергия и импульс фотона) с волновыми свойствами [частота (длина волны)]: E = hv, p = hv/c. Свет, обладая одновременно корпускулярно-волновыми свойствами, обнаруживает определенные закономерности в их проявлении. Так, волновые свойства света проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, а корпускулярные – в процессах взаимодействия света с веществом. Чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые свойства света И Наоборот Взаимосвязь между двойственными корпускулярно-волновыми свойствами света можно объяснить, если использовать, как это делает квантовая оптика, статистический подход к рассмотрению закономерностей распространения света. ГИПОТЕЗА ДЕ БРОЙЛЯ Луи де Бройль в 1924 г. постулировал, что корпускулярно-волновой дуализм имеет универсальный характер и распространяется не только на световые корпускулы (фотоны), но и на все частицы материи: частицы вещества (в частности, электроны) наряду с корпускулярными обладают также и волновыми свойствами. Количественные соотношения, связывающие корпускулярные (энергия и импульс) и волновые [частота (длина волны)] характеристики микрочастиц, такие же, как для фотона: E = hv = ħω, p = h/λ = ħk, где k = 2π/λ – волновое число, а ħ = h/2π – постоянная Планка. Длина волны, связанная с частицей, где р – импульс частицы, λ называется длиной волны де Бройля. Для нерелятивистской частицы длина волны де Бройля Для релятивистской частицы длина волны де Бройля
(в данном случае Если Т – кинетическая энергия частицы, то Е = Т + т0с2. Тогда Гипотеза де-Бройля была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Электрон при ударе о фотопластинку оказывает на нее такое же действие, как и фотон. Полученная таким способом электронограмма золота (рис. 61) сопоставлена с полученной в аналогичных условиях рентгенограммой алюминия (рис. 62). Сходство обеих картин поразительно. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что мы имеем дело с универсальным явлением – общим свойством материи Простейшей волной с частотой ω и волновым вектором k является плоская монохроматическая волна.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.008 с.) |

 , (72)
, (72) ,
, , (71)
, (71)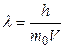 , где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то
, где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то  (71)
(71)
 ). Выразив с помощью соотношения
). Выразив с помощью соотношения  импульс частицы р через ее полную энергию Е, найдем
импульс частицы р через ее полную энергию Е, найдем 
 .
.


