
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прохождение частицы через одномерный потенциальный барьер.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим движение частицы в поле сил, которое может быть представлено в виде прямоугольного одномерного потенциального барьера конечной ширины l и высоты Uo (рис. 69). Подобный барьер описывается потенциальной энергией вида Предположим, что частица движется в положительном направлении оси х. Энергия частицы может быть как больше (Е> Uo), так и меньше (Е< Uo)высоты потенциального барьера. Случай 1: Е> Uo (рис. 70). По классической теории, частица преодолеет потенциальный барьер и попадет в область 3, где продолжает двигаться с той же энергией, а значит, и с той же скоростью, что и в области 1 (скорость частицы в области 2, естественно, меньше, так как здесь кинетическая энергия частицы T2 = E - U0).
Рассмотрим поведение квантовой частицы. В случае E > U0 уравнение Шредингера для стационарных состояний примет вид: для областей 1, 3 для области 2 Обозначив
где λ1,3 и λ2 – соответственно длины волн де Бройля в областях 1, 3 и 2, получим уравнения
Общие решения дифференциальных уравнений (125) и (126) для трех областей:
Как уже указывалось ранее, члены вида Тогда
В случае Е < Uo уравнение Шредингера для стационарных состояний примет вид: для областей 1, 3
для области 2 Общие решения дифференциальных уравнений (132) и (133) для трех областей:
В частности, для области 1 полная волновая функция имеет вид
Тогда Внутри барьера решение (135) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели экспонент не мнимые, а действительные. Однако теперь нельзя отбрасывать экспоненциально возрастающее решение, так как область, где U0 > E, имеет конечные размеры. Условия непрерывности волновой функции и ее первой производной в точках х = 0 и х = l [см. условия (131)] с учетом выражений (134), (135) и (137) приведут к уравнениям
Решая уравнения (138) и (139) относительно А2 и В2,получаем
Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер. Для описания туннельного эффекта используется коэффициент прозрачности D потенциального барьера, равный отношению плотности потока прошедших частиц n3 к плотности потока падающих n1. Учитывая что, (формулы приводятся без вывода) находим Тогда, согласно (140) получим, что где Do – постоянный множитель, который, как показывают точные расчеты, не очень отличается от единицы. Из формулы (141) следует, что коэффициент прозрачности (вероятность проникновения сквозь потенциальный барьер) быстро убывает с увеличением ширины барьера, а также с ростом его высоты. Теперь становится понятным рассматриваемое выше условие
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.61.142 (0.007 с.) |

 (121)
(121)
 , (121)
, (121) . (122)
. (122)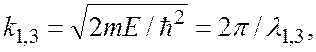 (123)
(123) , (124)
, (124) , (125)
, (125) . (126)
. (126)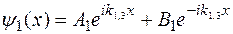 , (127)
, (127) , (128)
, (128) . (129)
. (129)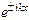 соответствуют плоским волнам, распространяющимся в положительном
соответствуют плоским волнам, распространяющимся в положительном  и отрицательном
и отрицательном  направлениях оси х (о волне как таковой можно говорить после умножения координатной части волновой функции на временной множитель
направлениях оси х (о волне как таковой можно говорить после умножения координатной части волновой функции на временной множитель  ).
). . (130)
. (130) (131)
(131) (для областей 1 и 3
(для областей 1 и 3  ), (132)
), (132) , где
, где  . (133)
. (133) , (134)
, (134) , (135)
, (135) . (136)
. (136)
 . (137)
. (137) ,
, ,
, , (138)
, (138) . (139)
. (139) ,
, .
. ,
, 
 . (140)
. (140) . Учитывая, что
. Учитывая, что  , запишем выражение для коэффициента прозрачности:
, запишем выражение для коэффициента прозрачности:  , (141)
, (141) , а именно оно определяет потенциальный барьер малой проницаемости.
, а именно оно определяет потенциальный барьер малой проницаемости.


