
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы геометрической оптики. Абсолютный и относительный показатели преломления. Явление полного внутреннего отражения.Содержание книги
Поиск на нашем сайте
Электромагнитная теория света. В первой трети XIX в. произошел переворот в оптических представлениях. В результате работ Т. Юнга (Англия) Уравнение Максвелла и О. Ж. Френеля (Франция) старая ньютоновская корпускулярная теория, рассматривавшая свет как поток светоносных частиц, была отвергнута. Возродились на новой основе и в новом физико-математическом истолковании представления Гюйгенса о свете как волновом движении эфира. Крупным достижением физики XIX в. была выдвинутая английским ученым Джемсом Кларком Максвеллом (1831—1879) электромагнитная теория света (1865 г.), обобщившая опыты и теоретические построения многих физиков различных стран в области электромагнетизма, термодинамики и оптики. Последователь Эрстедта и Фарадея, Максвелл разработал теорию электромагнитного поля. Математическим выражением нового учения явилась система уравнений, в равной мере относящихся как к электромагнитным, так и к оптическим явлениям и описывающих структуру электромагнитного поля. Из уравнений Максвелла в качестве основного следствия вытекал вывод о существовании электромагнитных волн, распространяющихся со скоростью света, и устанавливалась связь света с электромагнетизмом. Позднее существование электромагнитных волн было экспериментально доказано Генрихом Герцем (1857—1894) и явилось основой для всей радиотехники. Физико-математические построения Максвелла сыграли важную роль в дальнейшем развитии естествознания и техники. Однако теория Максвелла не давала исчерпывающей характеристики всех электромагнитных явлений. Максвелл, как и все физики XIX в., исходил еще из предположения о существовании эфира — последней из мнимых «невесомых жидкостей», которая пережила и флогистон и теплород, но которой в конце концов предстояло разделить их судьбу. В «Диалектике природы» Энгельс отмечал, что в области электричества еще предстоит сделать открытие, «подобное открытию Дальтона», т. е. атомистике, — открытие, «даю цее всей науке средоточие, а исследованию — прочную основу».(Ф Энгельс, Диалектика природы, стр. 84.) Прогноз Энгельса подтвердился, после того как была разработана электронная теория и учение об электричестве оказалось неразрывно связано с учением о строении атома.
Свет - электромагнитная волна, излучаемая атомами вещества. Электромагнитная волна представляет собой совокупность переменных электрического и магнитного полей, распространяющихся в пространстве со скоростью, v = 1/(m·m0·e·e0)1/2 =c/(m·e)1/2 Известно, что с = 3·108 м/с. В веществе скорость света v = c/n, Изменение электрического и магнитного поля волны происходят в одинаковой фазе. Электрические и магнитные поля перпендикулярны друг другу. Мгновенный снимок волны изображен на рисунке.
Кольца Ньютона. Кольца Ньютона. Являются классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей. В отраженном свете оптическая разность хода (с учетом потери половины при отражении), при условии что n=1, а I=0, где d — ширина зазора. r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая d=r2/2R. Следовательно,. Приравняв, к условиям максимума и минимума получим выражения для радиуса m-го светлого и темного колец: Измеряя радиусы соответствующих колец можно (зная радиус кривизны линзы) определить и наоборот, найти радиус кривизны линзы. Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны. Поэтому система светлых и темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску. Все рассуждения были приведены для отраженного света. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на /2. т.е. максимумам интерференции в отраженном свете соответствует минимумы в проходящем, и наоборот.
Как вариант:
Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклуюлинзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами
Дифракция от щели. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна
или
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.
С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол т (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно. Отметим, что дифракция на круглом отверстии и дифракция на диске впервые рассмотрены Френелем.
Как вариант: Бесконечно длинную щель можно образовать, расположив ряжом две обращенные в разные стороны полуплоскости. Следовательно, задача и дифракции Френеля от щели может быть решена с помощью спирали Карню. Волновую пов-ть падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу. Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку Р’, лежащую против края щели, начало результирующего вектора переместится в середину спирали О. Конец вектора переместится по спирали в направлении полюса F1. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (вектор, соответствующий точке Р’’). Интенсивность света при этом достигнет минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки Р в противоположное сторону, так как дифракционная картина симметрична относительно середины щели. Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (а) и отличные от нуля минимумы (б).
Формула Рэеля-Джинса и ультрофиолетовая катастрофа.Квантовая гипотеза и формула Планка. Формула Рэлея – Джинса для спектральной плотности энергетической светимости черного тела
где закон излучения Вина может быть записан в виде
Формула Рэлея – Джинса и закон Вина (имеется в виду закон излучения) – частные законы. Первая из них дает правильное спектральное распределение при малых частотах (hv<<kT), а второй – при больших частотах (hv>>kT). Они не дают общей картины распределения энергии по всему диапазону частот. Тогда средняя энергия осциллятора а спектральная плотность энергетической светимости черного тела Формула Планка для спектральной плотности энергетической светимости черного тела:
где h – постоянная Планка, k – постоянная Больцмана, c – скорость распространения света в вакууме. Из формулы Планка можно вывести частные законы, описывающие тепловое излучение.
Внешний фотоэффект. Внешний фотоэффект подчиняется следующим трем законам, полученным из обобщения опытных данных: I. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода за единицу времени, пропорционально интенсивности света. II. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой ν. III. Для каждого вещества существует «красная граница» фотоэффекта, т. е. минимальная частота v0 света (зависит от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен. Объяснение фотоэффекта дано на основе квантовой теории. Фотоэффект описывается уравнением Эйнштейна, выражающим закон сохранения энергии при фотоэффекте: т. е. энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону максимальной кинетической энергии. Подставляя в уравнение Эйнштейна (67) выражение (66), приходим к объяснению второго закона фотоэффекта
«Красная граница» зависит лишь от работы выхода электрона, т. е. от химической природы вещества и состояния его поверхности. Объяснение безынерционности фотоэффекта на основе квантовых представлений тривиально: испускание фотоэлектронов происходит сразу, как только на фотокатод падает излучение с ν > ν0.
Эффект Комптона. Эффект Комптона – упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ – излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Разность Δλ = λ' - λ (комптоновскип сдвиг) не зависит от длины волны λ падающего излучения и от природы рассеивающего вещества, а зависит только от угла θ между направлениями рассеянного и первичного излучений: где λc = h/(moc) – комптоновская длина волны электрона [ т0 – масса покоя электрона, λc = 2,42631058·10-12 м].
закон сохранения импульса p = p' + p или, используя теорему косинусов, закон сохранения энергии W0 + E = W + E', (70) где p = hv/c, p' = hv'/c, Wo = moc2 – энергия электрона до столкновения (m0 – масса покоя электрона), E = hv – энергия налетающего фотона,
ГИПОТЕЗА ДЕ БРОЙЛЯ Луи де Бройль в 1924 г. постулировал, что корпускулярно-волновой дуализм имеет универсальный характер и распространяется не только на световые корпускулы (фотоны), но и на все частицы материи: частицы вещества (в частности, электроны) наряду с корпускулярными обладают также и волновыми свойствами. Количественные соотношения, связывающие корпускулярные (энергия и импульс) и волновые [частота (длина волны)] характеристики микрочастиц, такие же, как для фотона: E = hv = ħω, p = h/λ = ħk, где k = 2π/λ – волновое число, а ħ = h/2π – постоянная Планка. Длина волны, связанная с частицей, где р – импульс частицы, λ называется длиной волны де Бройля. Для нерелятивистской частицы длина волны де Бройля Для релятивистской частицы длина волны де Бройля
(в данном случае Если Т – кинетическая энергия частицы, то Е = Т + т0с2. Тогда Гипотеза де-Бройля была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Электрон при ударе о фотопластинку оказывает на нее такое же действие, как и фотон. Полученная таким способом электронограмма золота (рис. 61) сопоставлена с полученной в аналогичных условиях рентгенограммой алюминия (рис. 62). Сходство обеих картин поразительно. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что мы имеем дело с универсальным явлением – общим свойством материи Простейшей волной с частотой ω и волновым вектором k является плоская монохроматическая волна. Спин Расщепление спектральных линий обусловлено расщеплением энергетических уровней. Для объяснения мультиплетности спектров американские физики (1925) Дж. Уленбек и С. Гаудсмит высказали гипотезу о том, что электрон обладает собственным механическим моментом импульса Ls, получившим название спина электрона. Спин электрона – квантовая величина, у нее нет классического аналога. Кроме того, оказалось, что существование спина и его свойств – прямое следствие уравнения Дирака, которое заменяет уравнение Шредингера в релятивистской квантовой механике. Согласно общим выводам квантовой механики, спин квантуется по закону где s – спиновое квантовое число. По аналогии с орбитальным моментом импульса, проекция Lsz спина квантуется так, что вектор Таким образом, собственный механический момент электрона принимает только одно значение: Проекция спина на направление внешнего магнитного поля в соответствии с (98) имеет вид где тs, – магнитное спиновое квантовое число. Проекция вектора не может быть больше модуля этого вектора, поэтому тs не должно по модулю превышать s, но тs может иметь разные знаки, откуда следует, что тs = ±s = ±1/2. (158) Таким образом, проекция собственного механического момента импульса электрона на ось z может принимать два значения: Спину электрона где величина называемая гиромагнитным отношением для спиновых моментов, оказалась на опыте в два раза больше, чем для орбитальных моментов [см. (152)]. Поэтому обычно говорят, что собственный механический момент (спин) электрона равен ½ (подразумевают в единицах ħ), а собственный (спиновый) магнитный момент равен одному магнетону Бора. Опыты Штерна и Герлаха Прямым доказательством существования спина электрона служат опыты Штерна и Герлаха (1921), в которых измерялись магнитные моменты атомов химических элементов именно, первой группы Периодической системы элементов. Это обусловлено тем, что для определения механического и магнитного моментов одного электрона необходимо использовать атомы, у которых механические (и магнитные) моменты всех электронов, кроме одного, компенсируют друг друга. Так как атомы первой группы Периодической системы имеют один валентный электрон, то моменты импульса и магнитные моменты этих атомов будут совпадать с моментами электрона. В опытах Штерна и Герлаха пучки нейтральных атомов (или молекул) в вакууме пропускались через область, в которой с помощью полюсных наконечников S и N специальной формы (рис. 77) создавалось магнитное поле, сильно неоднородное вблизи полюса S. Частицы пропускались вдоль оси у. В таком магнитном поле основная составляющая силы, действующей на атом,
пропорциональна z -составляющей магнитного момента и неоднородности магнитного поля Действительно, вдоль оси z (рис. 77) происходило расщепление пучка атомов серебра, щелочных металлов и водорода, но всегда наблюдалось только два пучка, одинаково отклоненных в противоположные стороны и расположенных симметрично относительно пучка в отсутствие магнитного поля. Это можно объяснить только тем, что магнитный момент валентного электрона при наличии поля может принимать два значения, одинаковых по модулю и противоположных по знаку. «Невероятность» данного результата заключается в том, что невозбужденные атомы серебра, щелочных металлов и водорода находятся в s -состоянии (l = 0). В этом состоянии момент импульса электрона Ll, равен нулю [см. 155]. Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту [см. (151)], поэтому он также равен нулю и магнитное поле не должно оказывать влияния на движение атомов, находящихся в основном состоянии, т. е. расщепления быть не должно. Кроме того, если бы в пучке были атомы в p состоянии (l = 1), то пучок должен был бы расщепиться на три компонента в соответствии с числом возможных значений магнитного квантового числа Таким образом, результаты опытов Штерна и Герлаха приводят к выводу, что расщепление в магнитном поле пучка атомов первой группы Периодической системы, заведомо находящихся в s-состоянии, на два компонента объясняется двумя возможными ориентациями спинового магнитного момента валентного электрона. Это хорошо согласуется с заключением о спине из спектроскопических данных [см. (157) и (158)].
Как уже рассматривалось ранее, состояние электрона в атоме можно однозначно описать, если воспользоваться любым набором четырех независимых квантовых чисел, например числами п, l, ml и ms. Эти числа могут принимать следующие значения: главное п = 1, 2, 3,... орбитальное l = 0, 1, 2,..., n - 1 магнитное ml = 0, ±1, ±2,..., ±l магнитное спиновое тs= ± 1/2. Согласно классической теории, электроны в основном (невозбужденном) состоянии атома должны занимать самый нижний, т. е. основной, энергетический уровень. Однако, как оказалось впоследствии, заполнение электронных оболочек атома подчиняется принципу, сформулированному Паули на основе обобщения опытных данных.
Билет 41 Теплоемкость твердых тел В качестве модели твердого тела рассмотрим правильно построенную кристаллическую решетку, в узлах которой частицы (атомы, ионы, молекулы), принимаемые за материальные точки, колеблются около своих положений равновесия — узлов решетки — в трех взаимно перпендикулярных направлениях. Таким образом, каждой составляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых, согласно закону равнораспределения энергии по степеням свободы (см. § 50), обладает энергией kT. Внутренняя энергия моля твердого тела
где NA— постоянная Авогадро; NAk=R (R — молярная газовая постоянная). Молярная теплоемкость твердого тела
т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом
состоянии одинакова (равна 3 R) и не зависит от температуры. Этот закон был эмпирически получен французскими учеными П. Дюлонгом (1785—1838) и Л. Пти (1791—1820) и носит название закона Дюлонга и Пти. Если твердое тело является химическим соединением (например, NaCl), то число частиц в моле не равно постоянной Авогадро, а равно nNA, где n — число атомов в молекуле (для NaCl число частиц в моле равно 2 NA, так, в одном моле NaCl содержится NA атомов Na и NA атомов Cl). Таким образом, молярная теплоемкость твердых химических соединений
т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение. Как показывают опытные данные (табл. 4), для многих веществ закон Дюлонга и Пти выполняется с довольно хорошим приближением, хотя некоторые вещества (С, Be, В) имеют значительные отклонения от вычисленных теплоемкостей. Кроме того, так же как и в случае газов (см. § 53), опыты по измерению теплоемкости твердых тел при низких температурах показали, что она зависит от температуры (рис. 113). Вблизи нуля кельвин теплоемкость тел пропорциональна Т 3, и только при достаточно высоких температурах, характерных для каждого вещества, выполняется условие (73.1). Алмаз, например, имеет теплоемкость, равную 3 R при1800 К! Однако для большинства твердых тел комнатная температура является уже достаточно высокой. Таблица 4
Расхождение опытных и теоретических значений теплоемкостей, вычисленных на основе классической теории, объяснили, исходя из квантовой теории теплоемкостей, А. Эйнштейн и П. Дебай. Билет 42 Понятие о квантовой теории теплоемкости. Фононы Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры (см. § 53). Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии (kT <<D E), то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному. Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т. е. D E вращ<<D E кол (см. § 230), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости (см. рис. 80). Функции распределения Ферми — Дирака для T =0 К и T >0 заметно различаются (рис. 312) лишь в узкой области энергий (порядка kT). Следовательно, в процессе нагревания металла участвует лишь незначительная часть всех электронов проводимости.Этим и объясняется отсутствие заметной разницы между теплоемкостями металлов и диэлектриков, что не могло быть объяснено классической теорией (см. § 103). Как уже указывалось (см. § 73), классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая статистика решила эту задачу. Так, А. Эйнштейн, приближенно считая, что колебания атомов кристаллической решетки независимы (модель кристалла как совокупности независимых колеблющихся с одинаковой частотой гармонических осцилляторов), создал качественную квантовую теорию теплоемкости кристаллической решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллической решетке не являются независимыми (рассмотрел непрерывный спектр частот гармонических осцилляторов). Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно-волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е= Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке — он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе. Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе — Эйнштейна (см. § 235), так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным; поэтому в формуле (235.1) для фононов необходимо m положить равным нулю. Применение статистики Бозе — Эйнштейна к фононному газу — газу из невзаимодействующих бозе-частиц — привело П. Дебая к количественному выводу, согласно которому при высоких температурах, когда T >> T D (классическая область), теплоемкость твердых тел описывается законом Дюлонга и Пти (см. § 73), а при низких температурах, когда T << T D (квантовая область), — пропорциональна кубу термодинамической температуры: СV~Т 3. В данном случае TD — характеристическая температура Дебая, определяемая соотношением kТD= Модель квазичастиц — фононов — оказалась эффективной для объяснения открытого П. Л. Капицей явления сверхтекучести жидкого гелия (см. § 31, 75). Теория сверхтекучести, созданная (1941) Л. Д. Ландау и развитая (1947) российским ученым Н. Н. Боголюбовым (р. 1909), применена впоследствии к явлению сверхпроводимости (см. § 239). Билет 43 Размер, состав и заряд атомного ядра. Массовое и зарядовое числа Э. Резерфорд, исследуя прохождение a-частиц с энергией в несколько мегаэлектрон-вольт через тонкие пленки золота (см. § 208), пришел к выводу о том, что атом состоит из положительно заряженного ядра и окружающих его электронов. Проанализировав эти опыты, Резерфорд также показал, что атомные ядра имеют размеры примерно 10–14 — 10–15 м (линейные размеры атома примерно 10–10 м). Атомное ядро состоит из элементарных частиц — протонов и нейтронов (протонно-нейтронная модель ядра была предложена российским физиком Д. Д. Иваненко (р. 1904), а впоследствии развита В. Гейзенбергом). Протон (р) имеет положительный заряд, равный заряду электрона, и массу покоя тр= 1,6726×10–27кг» 1836 тe, где тe — масса электрона. Нейтрон (n) — нейтральная частица с массой покоя тп= 1,6749×10–27кг»1839 тe. Протоны и нейтроны называются нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом Ze, где Z — зарядовое число ядра, равное числу протонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева. Известные в настоящее время 107 элементов таблицы Менделеева имеют зарядовые числа ядер от Z = 1 до Z = 107. Ядро обозначается тем же символом, что и нейтральный атом: Сейчас протонно-нейтронная модель ядра не вызывает сомнений. Рассматривалась также гипотеза о протонно-электронном строении ядра, но она не выдержала экспериментальной проверки. Так, если придерживаться этой гипотезы, то массовое число А должно представлять собой число протонов в ядре, а разность между массовым числом и числом электронов должна быть равна зарядовому числу. Эта модель согласовывалась со значениями изотопных масс и зарядов, но противоречила значениям спинов и магнитных моментов ядер, энергии связи ядра и т. д. Кроме того, она оказалась несовместимой с соотношением неопределенностей (см. § 215). В результате гипотеза о протонно-электронном строении ядра была отвергнута. Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. От числа же электронов зависит их распределение по состояниям в атоме, от которого, в свою очередь, зависят химические свойства атома. Следовательно, заряд ядра определяет специфику данного химического элемента, т.е. определяет число электронов в атоме, конфигурацию их электронных оболочек, величину и характер внутриатомного электрического поля. Ядра с одинаковыми Z, но разными А (т. е. с разными числами нейтронов N=A–Z) называются изотопами, а ядра с одинаковыми А, но разными Z — изобарами. Например, водород (Z =1) имеет три изотопа: Радиус ядра задается эмпирической формулой
где R 0 = (1,3¸1,7)10–15 м. Однако при употреблении этого понятия необходимо соблюдать осторожность (из-за его неоднозначности, например из-за размытости границы ядра). Из формулы (251.1) вытекает, что объем ядра пропорционален числу нуклонов в ядре. Следовательно, плотность ядерного вещества примерно одинакова для всех ядер (»1017 кг/м3).
Спин ядра и его магнитный момент Использование приборов высокой разрешающей способности и специальных источников возбуждения спектра позволило обнаружить сверхтонкую структуру спектральных линий. Ее существование В. Паули объяснил (1924) наличием у атомных ядер собственного момента импульса (спина) и магнитного момента. Собственный момент импульса ядра — спин ядра — складыва
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.016 с.) |






 (62)
(62) – средняя энергия осциллятора с собственной частотой ν. В области больших частот формула Рэлея – Джинса резко расходится с экспериментом, а также с законом смещения Вина. Кроме того, попытка получить закон Стефана – Больцмана из этой формулы дает абсурдный результат.
– средняя энергия осциллятора с собственной частотой ν. В области больших частот формула Рэлея – Джинса резко расходится с экспериментом, а также с законом смещения Вина. Кроме того, попытка получить закон Стефана – Больцмана из этой формулы дает абсурдный результат. (63)
(63) ,
,
 (64)
(64) (65)
(65) , (67)
, (67)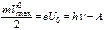 .
.
 , (68)
, (68)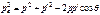 (69)
(69) – энергия электрона после столкновения E ' = hv' – энергия рассеянного фотона
– энергия электрона после столкновения E ' = hv' – энергия рассеянного фотона , (71)
, (71)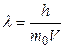 , где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то
, где т0 – масса покоя частицы. Если Т – кинетическая энергия частицы [ Т=р2/(2т) ], то  (71)
(71)
 ). Выразив с помощью соотношения
). Выразив с помощью соотношения  импульс частицы р через ее полную энергию Е, найдем
импульс частицы р через ее полную энергию Е, найдем 
 .
. (156)
(156) , может принимать 2s + 1 ориентации. Если с помощью спина объяснять расщепление спектральных линий, а значит и термов, на два подуровня, то следует предположить, что 2s+1=2, откуда
, может принимать 2s + 1 ориентации. Если с помощью спина объяснять расщепление спектральных линий, а значит и термов, на два подуровня, то следует предположить, что 2s+1=2, откуда  . Поскольку спиновое квантовое число имеет единственное значение
. Поскольку спиновое квантовое число имеет единственное значение 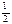 , то оно, не внося различия между состояниями, для их описания вместе с другими квантовыми числами обычно не используется.
, то оно, не внося различия между состояниями, для их описания вместе с другими квантовыми числами обычно не используется. , причем является такой же фундаментальной характеристикой электрона, как его заряд и масса.
, причем является такой же фундаментальной характеристикой электрона, как его заряд и масса.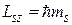 , (157)
, (157) .
. , соответствует собственный (спиновый) магнитный момент
, соответствует собственный (спиновый) магнитный момент  ,пропорциональный
,пропорциональный  , и направленный в противоположную сторону:
, и направленный в противоположную сторону:  , (159)
, (159) (160)
(160)
 (В — индукция магнитного поля). Так как сила зависит от
(В — индукция магнитного поля). Так как сила зависит от 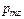 , то пучок частиц должен расщепиться на столько компонентов, сколько возможных проекций на ось z имеет магнитный момент. Если магнитный момент заряженной частицы обусловлен орбитальным моментом
, то пучок частиц должен расщепиться на столько компонентов, сколько возможных проекций на ось z имеет магнитный момент. Если магнитный момент заряженной частицы обусловлен орбитальным моментом 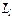 , то пучок должен расщепиться на 2l+1 компонентов.
, то пучок должен расщепиться на 2l+1 компонентов. .
.
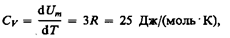 (73.1)
(73.1)
 . Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.
. Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах. , где
, где 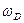 —предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113).
—предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113). , гдеХ — символхимического элемента, Z атомный номер (число протонов в ядре), А — массовоечисло (число нуклонов в ядре).
, гдеХ — символхимического элемента, Z атомный номер (число протонов в ядре), А — массовоечисло (число нуклонов в ядре). Н—протий (Z =1, N =0),
Н—протий (Z =1, N =0),  Н—дейтерий (Z =1, N =1),
Н—дейтерий (Z =1, N =1),  Н — тритий (Z =1, N =2), олово—десять, и т. д. В подавляющем большинстве случаев изотопы одного и того же химического элемента обладают одинаковыми химическими и почти одинаковыми физическими свойствами (исключение составляют, например, изотопы водорода), определяющимися в основном структурой электронных оболочек, которая является одинаковой для всех изотопов данного элемента. Примером ядер-изобар могут служить ядра
Н — тритий (Z =1, N =2), олово—десять, и т. д. В подавляющем большинстве случаев изотопы одного и того же химического элемента обладают одинаковыми химическими и почти одинаковыми физическими свойствами (исключение составляют, например, изотопы водорода), определяющимися в основном структурой электронных оболочек, которая является одинаковой для всех изотопов данного элемента. Примером ядер-изобар могут служить ядра  Ве,
Ве,  В,
В,  С. В настоящее время известно более 2500 ядер, отличающихся либо Z, либо А, либо тем и другим.
С. В настоящее время известно более 2500 ядер, отличающихся либо Z, либо А, либо тем и другим.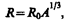 (251.1)
(251.1)


