
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитный момент атома. Атом в механическом поле. опыты Штерна и ГерлахаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Магнитный и механический моменты атомов обусловлены магнитным и механическим моментами орбитального движения электронов, а также собственными магнитными моментами и спинами электронов. Магнитные моменты и спины ядер здесь во внимание не принимаются, поскольку магнитные свойства атомов определяются в основном магнитными свойствами электронов. Электрон, движущийся по замкнутой орбите вокруг ядра, эквивалентен контуру с током
где S – площадь орбиты. Момент (149), обусловленный движением электрона по орбите, называют орбитальным магнитным моментом. Направление тока противоположно направлению движения электрона (рис. 76), а направление вектора С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса Ll, модуль которого
где т – масса электрона, r – радиус орбиты, v – скорость движения электрона по орбите (учли, что v=2πfr, S=πr2). Вектор L называемый орбитальным механическим моментом электрона образует с направлением его движения правовинтовую систему. Очевидно, что для проекций моментов pmz и Llz сохраняется та же связь: (Llz=ħml). Величину называют магнетоном Бора. Он является универсальной единицей измерения магнитных моментов. Возвращаясь к формуле (153), отметим, что проекция орбитального магнитного момента электрона на произвольную ось z может принимать только дискретные значения, т. е. квантуется, причем квантуется по тому же закону, что и проекция орбитального механического момента электрона (обе проекции, Модуль орбитального механического момента электрона
где l – орбитальное квантовое число.
Спин Расщепление спектральных линий обусловлено расщеплением энергетических уровней. Для объяснения мультиплетности спектров американские физики (1925) Дж. Уленбек и С. Гаудсмит высказали гипотезу о том, что электрон обладает собственным механическим моментом импульса Ls, получившим название спина электрона. Спин электрона – квантовая величина, у нее нет классического аналога. Кроме того, оказалось, что существование спина и его свойств – прямое следствие уравнения Дирака, которое заменяет уравнение Шредингера в релятивистской квантовой механике. Согласно общим выводам квантовой механики, спин квантуется по закону где s – спиновое квантовое число. По аналогии с орбитальным моментом импульса, проекция Lsz спина квантуется так, что вектор Таким образом, собственный механический момент электрона принимает только одно значение: Проекция спина на направление внешнего магнитного поля в соответствии с (98) имеет вид где тs, – магнитное спиновое квантовое число. Проекция вектора не может быть больше модуля этого вектора, поэтому тs не должно по модулю превышать s, но тs может иметь разные знаки, откуда следует, что тs = ±s = ±1/2. (158) Таким образом, проекция собственного механического момента импульса электрона на ось z может принимать два значения: Спину электрона где величина называемая гиромагнитным отношением для спиновых моментов, оказалась на опыте в два раза больше, чем для орбитальных моментов [см. (152)]. Поэтому обычно говорят, что собственный механический момент (спин) электрона равен ½ (подразумевают в единицах ħ), а собственный (спиновый) магнитный момент равен одному магнетону Бора. Опыты Штерна и Герлаха Прямым доказательством существования спина электрона служат опыты Штерна и Герлаха (1921), в которых измерялись магнитные моменты атомов химических элементов именно, первой группы Периодической системы элементов. Это обусловлено тем, что для определения механического и магнитного моментов одного электрона необходимо использовать атомы, у которых механические (и магнитные) моменты всех электронов, кроме одного, компенсируют друг друга. Так как атомы первой группы Периодической системы имеют один валентный электрон, то моменты импульса и магнитные моменты этих атомов будут совпадать с моментами электрона. В опытах Штерна и Герлаха пучки нейтральных атомов (или молекул) в вакууме пропускались через область, в которой с помощью полюсных наконечников S и N специальной формы (рис. 77) создавалось магнитное поле, сильно неоднородное вблизи полюса S. Частицы пропускались вдоль оси у. В таком магнитном поле основная составляющая силы, действующей на атом,
пропорциональна z -составляющей магнитного момента и неоднородности магнитного поля Действительно, вдоль оси z (рис. 77) происходило расщепление пучка атомов серебра, щелочных металлов и водорода, но всегда наблюдалось только два пучка, одинаково отклоненных в противоположные стороны и расположенных симметрично относительно пучка в отсутствие магнитного поля. Это можно объяснить только тем, что магнитный момент валентного электрона при наличии поля может принимать два значения, одинаковых по модулю и противоположных по знаку. «Невероятность» данного результата заключается в том, что невозбужденные атомы серебра, щелочных металлов и водорода находятся в s -состоянии (l = 0). В этом состоянии момент импульса электрона Ll, равен нулю [см. 155]. Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту [см. (151)], поэтому он также равен нулю и магнитное поле не должно оказывать влияния на движение атомов, находящихся в основном состоянии, т. е. расщепления быть не должно. Кроме того, если бы в пучке были атомы в p состоянии (l = 1), то пучок должен был бы расщепиться на три компонента в соответствии с числом возможных значений магнитного квантового числа Таким образом, результаты опытов Штерна и Герлаха приводят к выводу, что расщепление в магнитном поле пучка атомов первой группы Периодической системы, заведомо находящихся в s-состоянии, на два компонента объясняется двумя возможными ориентациями спинового магнитного момента валентного электрона. Это хорошо согласуется с заключением о спине из спектроскопических данных [см. (157) и (158)].
Как уже рассматривалось ранее, состояние электрона в атоме можно однозначно описать, если воспользоваться любым набором четырех независимых квантовых чисел, например числами п, l, ml и ms. Эти числа могут принимать следующие значения: главное п = 1, 2, 3,... орбитальное l = 0, 1, 2,..., n - 1 магнитное ml = 0, ±1, ±2,..., ±l магнитное спиновое тs= ± 1/2. Согласно классической теории, электроны в основном (невозбужденном) состоянии атома должны занимать самый нижний, т. е. основной, энергетический уровень. Однако, как оказалось впоследствии, заполнение электронных оболочек атома подчиняется принципу, сформулированному Паули на основе обобщения опытных данных.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , где f – частота вращения электрона по орбите, е – абсолютная величина заряда электрона. Орбитальному току соответствует магнитный момент
, где f – частота вращения электрона по орбите, е – абсолютная величина заряда электрона. Орбитальному току соответствует магнитный момент  , модуль которого
, модуль которого , (149)
, (149) образует левовинтовую систему с направлением движения электрона (заряд электрона – отрицательный), причем вектор
образует левовинтовую систему с направлением движения электрона (заряд электрона – отрицательный), причем вектор  перпендикулярен плоскости орбиты электрона.
перпендикулярен плоскости орбиты электрона. (150)
(150)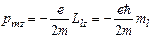
 (153)
(153)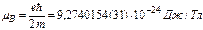 (154)
(154) и
и  , определяются одним и тем же магнитным квантовым числом тl,).
, определяются одним и тем же магнитным квантовым числом тl,). , (155)
, (155) .
. (156)
(156) , может принимать 2s + 1 ориентации. Если с помощью спина объяснять расщепление спектральных линий, а значит и термов, на два подуровня, то следует предположить, что 2s+1=2, откуда
, может принимать 2s + 1 ориентации. Если с помощью спина объяснять расщепление спектральных линий, а значит и термов, на два подуровня, то следует предположить, что 2s+1=2, откуда  . Поскольку спиновое квантовое число имеет единственное значение
. Поскольку спиновое квантовое число имеет единственное значение 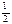 , то оно, не внося различия между состояниями, для их описания вместе с другими квантовыми числами обычно не используется.
, то оно, не внося различия между состояниями, для их описания вместе с другими квантовыми числами обычно не используется. , причем является такой же фундаментальной характеристикой электрона, как его заряд и масса.
, причем является такой же фундаментальной характеристикой электрона, как его заряд и масса.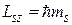 , (157)
, (157) .
. , соответствует собственный (спиновый) магнитный момент
, соответствует собственный (спиновый) магнитный момент  ,пропорциональный
,пропорциональный  , и направленный в противоположную сторону:
, и направленный в противоположную сторону:  , (159)
, (159) (160)
(160)
 (В — индукция магнитного поля). Так как сила зависит от
(В — индукция магнитного поля). Так как сила зависит от 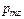 , то пучок частиц должен расщепиться на столько компонентов, сколько возможных проекций на ось z имеет магнитный момент. Если магнитный момент заряженной частицы обусловлен орбитальным моментом
, то пучок частиц должен расщепиться на столько компонентов, сколько возможных проекций на ось z имеет магнитный момент. Если магнитный момент заряженной частицы обусловлен орбитальным моментом 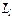 , то пучок должен расщепиться на 2l+1 компонентов.
, то пучок должен расщепиться на 2l+1 компонентов. .
.


