
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон электромагнитной индукции. Правило ЛенцаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Явление электромагнитной индукции было открыто Фарадеем в 1831 году. Опыты Фарадея показали, что во всяком замкнутом проводящем контуре при изменении числа линий магнитной индукции, проходящих через него, возникает электрический ток. Этот ток был назван индукционным током. Например, в момент вдвигания магнита и в момент его выдвигания из катушки наблюдается отклонение стрелки гальванометра. Отклонения стрелки при вдвигании и выдвигании противоположны. Отклонения тем больше, чем быстрее двигается магнит. Если вдвигать и выдвигать магнит в катушку другим полюсом, то отклонения стрелки будут противоположны первоначальным
В другом опыте одна из катушек К1 находится внутри другой катушки К2. В момент включения или выключения тока через катушку К1, или при его изменении, или при перемещении катушек относительно друг друга наблюдается отклонение стрелки гальванометра, если по К1 протекает ток.
Полное число линий магнитной индукции через площадь контура представляет собой магнитный поток. Таким образом, причиной возникновения индукционного тока является изменение магнитного потока через контур. Если контур расположен в однородном магнитном поле, индукция которого равна В, то магнитный поток через контур, площадь которого S: Φ = B·S·cosα (3.10) Где α угол между вектором В и нормалью n к поверхности контура.
Магнитный поток – скалярная величина. Если линии вектора В выходят из площадки, то магнитный поток считается положительным, если входят в неё – отрицательным. В системе СИ единицей магнитного потока является вебер (Вб). Один вебер – это магнитный поток, создаваемый однородным магнитным полем индукцией 1Тл сквозь площадку 1м², перпендикулярную линиям индукции. 1Вб = 1Тл·м². Возникновение индукционного тока означает, что при изменении магнитного потока Φ в контуре возникает ЭДС индукции. Она определяется скоростью изменения магнитного потока, т.е. е = – ΔΦ / Δt (3.11) Формула (3.11) выражает закон Фарадея. Знак минус есть математическое выражение правила Ленца, которое гласит, что индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей. Иначе говоря: Индукционный ток создаёт магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
48.Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе. Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной.
Иногда бывает полезно также ввести понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных килограммах (кг−1). Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль−1). Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией Обычно обозначается греческой буквой В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как
и
Для изотропных веществ соотношение:
можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру). В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:
где Граничные условия получаются из уравнений Максвелла предельным переходом. Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме.
где
где Эти граничные условия показывают непрерывность нормальной компоненты вектора магнитной индукции (нормальная компонента электрической индукции непрерывна только при отсутствии на границе поверхностных зарядов). Из уравнения непрерывности можно получить граничное условие для токов:
Важным частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. В результате тангенциальная компонента электрического и нормальная магнитного поля на границе с идеальным проводником равны нулю:
47. Теорема о циркуляции магнитного поля — циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. В математической формулировке для магнитостатики теорема имеет следующий вид:
Здесь
Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса. Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики). Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности
Тогда теорема о циркуляции запишется в форме
где под В динамическом случае - то есть в общем случае классической электродинамики - когда поля меняются во времени (а в средах при этом меняется и их поляризация) - и речь тогда идет об обобщенной теореме, включающей Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M. В СИ: В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ. В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было». Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором B 0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах. При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо). Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля[1]. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна. молекулах. В магнетике на магнитное поле макротоков (внешнее магнитное поле) накладывается дополнительное поле микротоков(внутреннее). Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества:
Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём. В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как
и является функцией координат. Связь между M и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):
где χ m называют магнитной восприимчивостью. В ферромагнитных материалах нет однозначной связи между M и H из-за магнитного гистерезиса. Магнитная индукция определяется через намагниченность как:
45. Строение атомов и молекул. Намагничивание вещества. Моле́кула (новолат. molecula, уменьшительное от лат. moles — масса) — электрически нейтральная частица, образованная из двух или более связанных ковалентными связями атомов, наименьшая частица химического вещества. В физике к молекулам причисляют также одноатомные молекулы, то есть свободные (химически не связанные) атомы (например, инертных газов, ртути и т. п.). Причисление к молекулам одноатомных молекул, то есть свободных атомов, например одноатомных газов, приводит к совмещению понятий «молекула» и «атом». С точки зрения квантовой механики молекула представляет собой систему не из атомов, а из электронов и атомных ядер, взаимодействующих между собой. Молекулы и макромолекулы подавляющего большинства химических соединений являются диамагнитными. Магнитная восприимчивость молекул (χ) для отдельных органических соединений может быть выражена как сумма значений χ для отдельных связей. Молекулы, имеющие постоянный магнитный момент, является парамагнитными. К таковым относятся молекулы с нечетным количеством электронов на внешней оболочке (например, NO и любые свободные радикалы), молекулы, содержащие атомы с незаполненными внутренними оболочками (переходные металлы и т. д.). Магнитная восприимчивость парамагнитных веществ зависит от температуры, поскольку тепловое движение препятствует ориентации магнитных моментов в магнитном поле. А́том (от др.-греч. ἄτομος — неделимый) — частица вещества микроскопических размеров и массы, наименьшая часть химического элемента, являющаяся носителем его свойств. Атом состоит из атомного ядра и электронов. Если число протонов в ядре совпадает с числом электронов, то атом в целом оказывается электрически нейтральным. В противном случае он обладает некоторым положительным или отрицательным зарядом и называется ионом. В некоторых случаях под атомами понимают только электронейтральные системы, в которых заряд ядра равен суммарному заряду электронов, тем самым противопоставляя их электрически заряженным ионам. Ядро, несущее почти всю (более чем 99,9 %) массу атома, состоит из положительно заряженных протонов и незаряженных нейтронов, связанных между собой при помощи сильного взаимодействия. Атомы классифицируются по количеству протонов и нейтронов в ядре: число протонов Z соответствует порядковому номеру атома в периодической системе и определяет его принадлежность к некоторому химическому элементу, а число нейтронов N — определённому изотопу этого элемента. Число Z также определяет суммарный положительный электрический заряд (Ze) атомного ядра и число электронов в нейтральном атоме, задающее его размер. Считается, что при намагничивании тело приобретает магнитный дипольвый момент Рм = qMl, где qu — магнитный заряд тела, а l — расстояние между положительным (северным) и отрицательным (южным) зарядами. Магнитный момент единицы объема вещества М = pJV (V — объем тела) называют намагниченностью. Как правило, намагниченность прямо пропорциональна напряженности вызвавшего её магнитного поля Н. Коэффициент пропорциональности к называют магнитной восприимчивостью вещества. Чем больше к, тем лучше намагничивается данный материал. В технике способность вещества намагничиваться чаще характеризуют магнитной проницаемостью f. Исходя из того, что магнитная индукция В = Цо(Н + М) = f., абсолютная магнитная проницаемость вещества f = f.o(1 + к). Величину = 1 + к называют относительной магнитной проницаемостью. По значению к и fL все вещества делят на диамагнетики, парамагнетики и ферромагнетики. Исходя из того, что никаких магнитных зарядов (монополей) у намагниченных тел не существует, их представление, не верно. В намагниченном теле реальны лишь круговые токи, которые создают МП подобное полю диполя. Это показал ещё Ампер, поэтому токи и получили название токов Ампера. Токи Ампера /А представляют собой векторную сумму молекулярных токов, обусловленных вращением электронов вокруг своей оси и вокруг ядра атома, а также вращением ядерной материи. 44. Магнитная энергия тока. Объемная плотность энергии магнитного поля. Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф =LI, причем при изменении тока на d I магнитный поток изменяется на dФ= L d I. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу d А=I dФ =LI d I. Тогда работа по созданию магнитного потока Ф будет равна Следовательно, энергия магнитного поля, связанного с контуром,
Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля. Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим
Так как I=Bl/ (m 0 mN) (см. (119.2)) и В=m 0 mH (см. (109.3)), то
где Sl = V — объем соленоида. Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.
54. Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Дифференциальная форма Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций ( Закон Гаусса Закон Гаусса для магнитного поля Закон индукции Фарадея Теорема о циркуляции магнитного поля Введённые обозначения: · · · · · · · ·
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины Интегральная форма Закон Гаусса Закон Гаусса для магнитного поля Закон индукции Фарадея Теорема о циркуляции магнитного поля Введённые обозначения: · · · При интегрировании по замкнутой поверхности вектор элемента площади Словесное описание законов Максвелла, например, закона Фарадея, несёт отпечаток традиции, поскольку вначале при контролируемом изменении магнитного потока регистрировалось возникновение электрического поля (точнее электродвижущей силы). В общем случае в уравнениях Максвелла (как в дифференциальной, так и в интегральной форме) векторные функции
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1084; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.149 (0.017 с.) |





 , где
, где  — намагниченность вещества под действием магнитного поля,
— намагниченность вещества под действием магнитного поля, 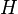 — напряженность магнитного поля.
— напряженность магнитного поля. и напряжённостью магнитного поля
и напряжённостью магнитного поля  . Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).


 ,
, — относительная, а
— относительная, а  — магнитная постоянная (магнитная проницаемость вакуума).
— магнитная постоянная (магнитная проницаемость вакуума). ,
, ,
, — единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,
— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,  — плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных итп токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).
— плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных итп токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе). ,
, ,
, — поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды).
— поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды). ,
, ,
, ,
, ,
,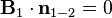 ,
,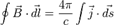
 — вектор магнитной индукции,
— вектор магнитной индукции,  — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме[4]:
— плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме[4]:
 и введя вектор напряжённости магнитного поля
и введя вектор напряжённости магнитного поля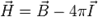


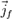 (в отличие от
(в отличие от  в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку
в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку 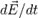 , - всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене
, - всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене  .
. где
где 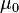 — магнитная постоянная.
— магнитная постоянная.


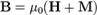 (в системе СИ)
(в системе СИ)
 (130.1)
(130.1)
 (130.2)
(130.2)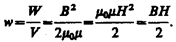 (130.3)
(130.3) ):
): Электрический заряд является источником электрической индукции.
Электрический заряд является источником электрической индукции. Не существуетмагнитных зарядов.
Не существуетмагнитных зарядов. Изменение магнитной индукции порождает вихревое электрическое поле.
Изменение магнитной индукции порождает вихревое электрическое поле.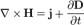 Электрический ток и изменение электрической индукции порождают вихревое магнитное поле
Электрический ток и изменение электрической индукции порождают вихревое магнитное поле — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);
— плотность стороннего электрического заряда (в единицах СИ — Кл/м³); — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как
— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как  , где
, где  — (средняя)скорость движения этих носителей в окрестности данной точки,
— (средняя)скорость движения этих носителей в окрестности данной точки, 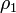 — плотность заряда этого типа носителей (она в общем случае не совпадает с
— плотность заряда этого типа носителей (она в общем случае не совпадает с  — скорость света в вакууме (299 792 458 м/с);
— скорость света в вакууме (299 792 458 м/с); — напряжённость электрического поля (в единицах СИ — В/м);
— напряжённость электрического поля (в единицах СИ — В/м); — напряжённость магнитного поля (в единицах СИ — А/м);
— напряжённость магнитного поля (в единицах СИ — А/м); — электрическая индукция (в единицах СИ — Кл/м²);
— электрическая индукция (в единицах СИ — Кл/м²); — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1); — дифференциальный оператор набла, при этом:
— дифференциальный оператор набла, при этом: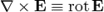 означает ротор вектора,
означает ротор вектора, означает дивергенцию вектора.
означает дивергенцию вектора. ,
,  ,
,  и
и  и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
и учитывающие индивидуальные свойства среды, называются материальными уравнениями. Поток электрической индукции через замкнутую поверхность
Поток электрической индукции через замкнутую поверхность  пропорционален величине свободного заряда, находящегося в объёме
пропорционален величине свободного заряда, находящегося в объёме  , который окружает поверхность
, который окружает поверхность  Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).
Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).
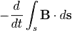 Изменениепотока магнитной индукции, проходящего через незамкнутую поверхность
Изменениепотока магнитной индукции, проходящего через незамкнутую поверхность  , который является границей поверхности
, который является границей поверхности 
 Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность
Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность  — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём
— двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём 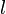 ).
). — электрический заряд, заключённый в объёме
— электрический заряд, заключённый в объёме  — электрический ток, проходящий через поверхность
— электрический ток, проходящий через поверхность  направлен из объёма наружу. Ориентация
направлен из объёма наружу. Ориентация  при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по
при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по  .
. являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.


