
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность поля заряженной плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
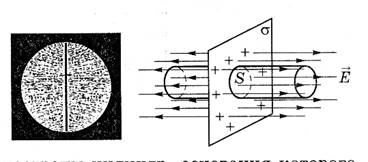
Бесконечная плоскость, заряженная с поверхностной плотностью заряда
Ф= Приравняем правые части уравнений:
Выразим
Найдем напряженность электрического поля между разноименно заряженными пластинами с одинаковой поверхностной плотностью:
Найдем поле вне пластин:
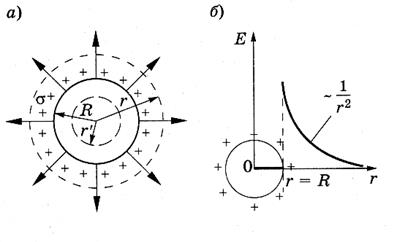
Напряженность поля заряженной сферы
Ф=
Ф=ES (3) для r < R
Для r = R ( Для r > R
Напряженность поля, созданного шаром, заряженным равномерно по всему объему Объемная плотность заряда,
Для r < R ( Для r = R
Для r > R
8. РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА Электростатическое поле - эл. поле неподвижного заряда.
Работа поля (эл. силы) не зависит от формы траектории и на замкнутой траектории = нулю.
Теорема о циркуляции для электростатического поля. Поскольку электростатическое поле является центральным, то силы, действующие на заряд в таком поле, являются консервативными. Так как
9. Потенциал Система "заряд - электростатическое поле" или "заряд - заряд" обладает потенциальной энергией, подобно тому, как система "гравитационное поле - тело" обладает потенциальной энергией. Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал - это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией. Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной. Потенциальная энергия поля - это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом. Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице. Разность потенциалов Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Принцип суперпозиции Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора. Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:
Энергия электростатического поля системы точечных зарядов равна:
10. Равномерно заряженная плоскость.
Из условий симметрии следует, что вектор E везде перпендикулярен плоскости. Кроме того, в симметричных относительно плоскости точках вектор E будет одинаков по величине и противоположен по направлению.
где
Когда напряженность поля не зависит от расстояния между плоскостями, такое поле называют однородным. График зависимости E (x) для плоскости.
Разность потенциалов между двумя точками, находящимися на расстояниях R 1 и R 2от заряженной плоскости, равна
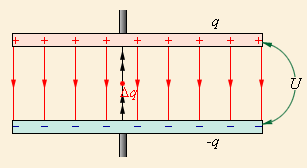
Пример 2. Две равномерно заряженные плоскости.
Разность потенциалов между плоскостями
Пример 3. Тонкий заряженный стержень.
Для расчета напряженности поля в произвольной точке, находящейся на расстоянии r от оси стержня, проведём через эту точку цилиндрическую поверхность
По теореме Гаусса, поток вектора E равен алгебраической сумме электрических зарядов, находящихся внутри поверхности (в данном случае цилиндра) делённой на произведение электрической постоянной
где
Разность потенциалов электрического поля между двумя точками, находящимися на расстояниях R 1 и R 2 от оси стержня, найдём, пользуясь связью между напряжённостью и потенциалом электрического поля. Так как напряжённость поля изменяется только в радиальном направлении, то
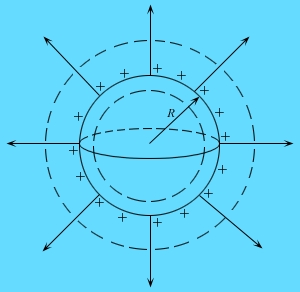
Пример 4. Заряженная сферическая поверхность.
Линии напряжённости направлены по радиусам от центра сферы, а модуль вектора E зависит только от расстояния r от центра сферы. Для расчёта поля выберем замкнутую сферическую поверхность радиуса r.
где
Напряжённость уменьшается по тому же закону, что и напряженность поля точечного заряда, т. е. по закону
Пример 5. Заряженный по объему шар из диэлектрика.
При r < R (внутри шара)
Вне шара (r > R) потенциал электрического поля меняется по закону
Внутри шара (r < R) потенциал описывается выражением
В заключение, приведем выражения для расчета напряженностей полей заряженных тел, различной формы
11.
12. Проводник – это твердое тело, в котором имеются “свободные электроны”, перемещающиеся в пределах тела. Металлические проводники в целом являются нейтральными: в них поровну отрицательных и положительных зарядов. Положительно заряженные – это ионы в узлах кристаллической решетки, отрицательные – электроны, свободно перемещающиеся по проводнику. Когда проводнику сообщают избыточное количество электронов, он заряжается отрицательно, если же у проводника «отбирают» какое-то количество электронов, он заряжается положительно. Избыточный заряд распределяется только по внешней поверхности проводника.
1. Напряженность поля в любой точке внутри проводника равна нулю. 2. Вектор на поверхности проводника направлен по нормали к каждой точке поверхности проводника. Действительно, если бы условие 1 не выполнялось, то подвижные носители электрических зарядов, имеющиеся в каждом проводнике, под действием сил поля пришли бы в движение (в проводнике возник бы электрический ток) и равновесие было бы нарушено. Из 1 следует, что поскольку Из того факта, что поверхность проводника эквипотенциальна следует, что непосредственно у этой поверхности поле направлено по нормали к ней в каждой точке (условие 2). Если бы это было не так, то под действием касательной составляющей заряды пришли бы в движение по поверхности проводника. т.е. равновесие зарядов на проводнике было бы невозможным. Из 1 следует, что поскольку Внутри проводника избыточных зарядов нет. Заряды распределяются только на поверхности проводника с некоторой плотностью s и находятся в очень тонком поверхностном слое (его толщина около одного-двух межатомных расстояний). 13. Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды. 14. Общая задача электростатики Вектор напряженности по теореме Гаусса
В случае
Пусть известны граничные условия на поверхностях проводников: значения При решении задачи определяется значение Рассмотрим пример. Найдем напряженность в пустой полости проводника. Потенциал в полости удовлетворяет уравнению Лапласа; потенциал на стенках проводника Решение уравнения Лапласа в этом случае тривиальное, и по теореме единственности других решений нет
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает · электростатическое поле, · стационарное поле температуры, · поле давления, · поле потенциала скорости в гидродинамике. Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона. Это уравнение имеет вид: где В трёхмерной декартовой системе координат уравнение принимает форму:
В декартовой системе координат оператор Лапласа записывается в форме
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод». 15.
16. Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накоплениязаряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Мкость Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад. Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга, в системе СИ выражается формулой: Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади. При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения. Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов. [править]Удельная ёмкость Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя. 18. В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 19597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.011 с.) |

 (1)
(1)
 (2)
(2) : для расчета напряженности электрического поля, созданного бесконечной плоскостью, выделим в пространстве цилиндр, ось которого перпендикулярна заряженной плоскости, а основания – параллельны ей и одно из оснований проходит через интересующую нас точку поля. Согласно теореме Гаусса поток вектора напряженности электрического поля сквозь замкнутую поверхность равен:
: для расчета напряженности электрического поля, созданного бесконечной плоскостью, выделим в пространстве цилиндр, ось которого перпендикулярна заряженной плоскости, а основания – параллельны ей и одно из оснований проходит через интересующую нас точку поля. Согласно теореме Гаусса поток вектора напряженности электрического поля сквозь замкнутую поверхность равен: , с другой стороны он же: Ф=E
, с другой стороны он же: Ф=E 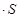
 =
=  - через поверхностную плотность заряда и найдем напряженность электрического поля:
- через поверхностную плотность заряда и найдем напряженность электрического поля:



 (1)
(1) (2)
(2) (3)
(3) ;
;  (4)
(4)
 ;
;  , т.к.
, т.к.  (внутри сферы нет зарядов)
(внутри сферы нет зарядов) ;
;  ;
;  )
) 

 распределенного по шару:
распределенного по шару: (1)
(1)
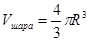 (2)
(2)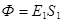 ; Ф=
; Ф=  )
) 

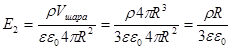



 Так как d l /cosα=dr, то
Так как d l /cosα=dr, то  Работа при перемещении заряда Q0 из точки 1 в точку 2
Работа при перемещении заряда Q0 из точки 1 в точку 2  (1) от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е.
(1) от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е. 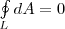 (2) Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = E l d l, где E l = Ecosα — проекция вектора Е на направление элементарного перемещения. Тогда формулу (2) можно представить в виде
(2) Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = E l d l, где E l = Ecosα — проекция вектора Е на направление элементарного перемещения. Тогда формулу (2) можно представить в виде  (3) Интеграл
(3) Интеграл  называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называетсяпотенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность. Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля).
называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называетсяпотенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность. Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля).
 представляет собой элементарную работу, которую силы поля производят над единичным зарядом, то работа консервативных сил на замкнутом контуре равна
представляет собой элементарную работу, которую силы поля производят над единичным зарядом, то работа консервативных сил на замкнутом контуре равна


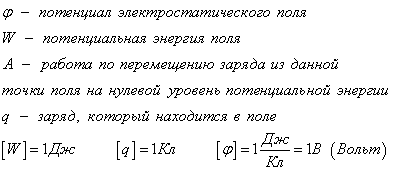



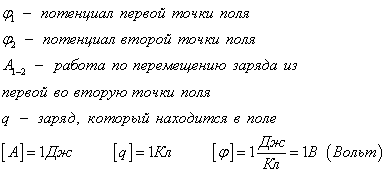





 , можно рассчитать, воспользовавшись теоремой Гаусса.
, можно рассчитать, воспользовавшись теоремой Гаусса.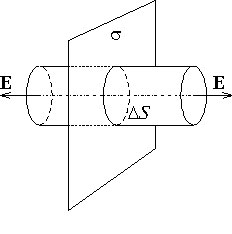
 ,
, - площадь основания цилиндра. Цилиндр вырезает из плоскости заряд
- площадь основания цилиндра. Цилиндр вырезает из плоскости заряд  . Если плоскость находится в однородной изотропной среде с относительной диэлектрической проницаемостью
. Если плоскость находится в однородной изотропной среде с относительной диэлектрической проницаемостью  , то
, то .
.

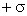 и
и  . Напряженность поля найдем как суперпозицию напряжённостей полей каждой из плоскостей. Электрическое поле отлично от нуля только в пространстве между плоскостями и равно
. Напряженность поля найдем как суперпозицию напряжённостей полей каждой из плоскостей. Электрическое поле отлично от нуля только в пространстве между плоскостями и равно  .
.
 , где d - расстояние между плоскостями.
, где d - расстояние между плоскостями. 
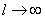 заряженным с линейной плотностью заряда
заряженным с линейной плотностью заряда  стержнем, используем теорему Гаусса.
стержнем, используем теорему Гаусса.
 ,
, и относительной диэлектрической проницаемости среды
и относительной диэлектрической проницаемости среды 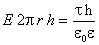 ,
, заряд той части стержня, которая находится внутри цилиндра. Следовательно, напряжённость электрического поля
заряд той части стержня, которая находится внутри цилиндра. Следовательно, напряжённость электрического поля .
.
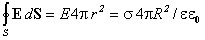 ,
,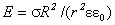 .
. .
.  .
. .
. 
 равномерно заряжен по объёму с плотностью
равномерно заряжен по объёму с плотностью  , то создаваемое им электрическое поле также является центрально-симметричным.
, то создаваемое им электрическое поле также является центрально-симметричным.  .
.  , так что
, так что .
. , поток вектора E через поверхность будет определяться зарядом
, поток вектора E через поверхность будет определяться зарядом  .
. 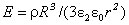 .
.  ).
).
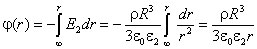 .
. .
.


 Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.



 ,
,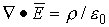
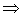
 - уравнение Пуассона.
- уравнение Пуассона. - нет зарядов между проводниками, получаем
- нет зарядов между проводниками, получаем - уравнение Лапласа.
- уравнение Лапласа. ; тогда данная задача имеет единственное решение согласно теореме единственности.
; тогда данная задача имеет единственное решение согласно теореме единственности. и затем поле
и затем поле  между проводниками
между проводниками  .
.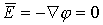 , т.е. поля в полости проводника нет.
, т.е. поля в полости проводника нет.
 — оператор Лапласа или лапласиан, а
— оператор Лапласа или лапласиан, а  — вещественная или комплексная функция на некотором многообразии.
— вещественная или комплексная функция на некотором многообразии.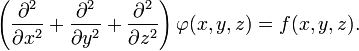
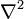 и уравнение Пуассона принимает вид:
и уравнение Пуассона принимает вид: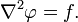

 Величину
Величину  (1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен
(1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен  Применяя формулу (1), получим, что емкость шара
Применяя формулу (1), получим, что емкость шара  , где
, где  —относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице),
—относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице),  — электрическая постоянная, численно равная 8,854187817·10−12 Ф/м. Эта формула справедлива, лишь когда d много меньше линейных размеров пластин.
— электрическая постоянная, численно равная 8,854187817·10−12 Ф/м. Эта формула справедлива, лишь когда d много меньше линейных размеров пластин.
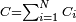 или
или 

 или
или 




