
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле равномерно заряженной бесконечной плоскостиСодержание книги
Поиск на нашем сайте
а) выбор гауссовой поверхности:
б) считаем Σqi внутри "гауссова ящика": очевидно,
в) приравниваем результат, полученный в пункте а), к результату пункта б), деленному на ε0:
Выражаем E:
Поле равномерно заряженной бесконечной плоскости однородно. Поле плоского конденсатора По 9.3.6.
Поле однородно заряженного бесконечного цилиндра
Поле однородно заряженной сферы
Поле объемного заряженного шара
Работа электростатического поля
Из (5.3.2), (5.3.3):
Работа электрического поля точечного заряда Пусть Е создается точечным зарядом q, тогда из (9.3.7)
из (5.3.3):
Потенциал - энергетическая характеристика поля Потенциал электростатического поля в точке r равен отношению потенциальной
φ - не зависит от q'! Единица потенциала - 1 вольт (1 В)
Разность потенциалов, связь с работой
Потенциал поля точечного заряда Из (9.5.1)
Из (9.6.2)
Значит, потенциал поля, создаваемого точечным зарядом q:
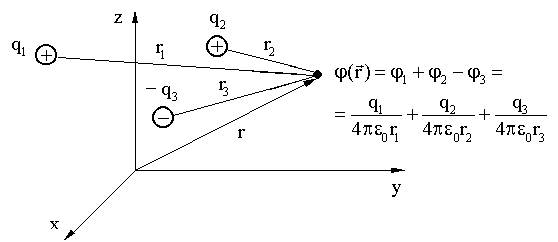
Потенциал поля системы точечных зарядов
В общем случае:
здесь qi - алгебраические величины. Электрон-вольт - внесистемная единица работы
Связь между напряженностью и потенциалом
а) через напряженность, из (5.3.2), (9.3.5)
б) через разность потенциалов (9.6.2):
Приравнивая, получим:
Возьмем
Для
Для
Вектор напряженности:
Обозначим
Это оператор градиента, или оператор Гамильтона. Тогда
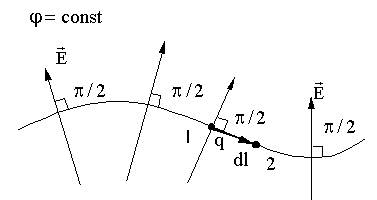
9.8. Эквипотенциальная поверхность (лат. aequus - равный) - поверхность, все точки которой имеют одинаковый потенциал, т.е.
Перемещаем заряд q вдоль эквипотенциальной поверхности:
См. (9.6.2), (9.5) Линии напряженности перпендикулярны эквипотенциальным поверхностям.
Проводник в электрическом поле Проводник?
В проводнике, из-за столкновений с ионами, средняя дрейфовая скорость электронов порядка 1мм/с, но скорость распространения электрического поля с=3·108 м/с. Условия равновесия зарядов на проводнике Равновесие -
Проводник во внешнем электрическом поле Мысленный опыт:
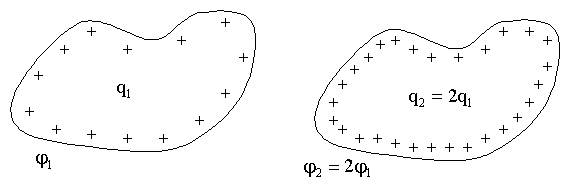
Электроемкость уединенного проводника
Таким образом:
Электроемкость конденсатора Конденсатор - это два проводника, обычно плоской цилиндрической или сферической формы, расположенные на небольшом расстоянии друг от друга. Проводники, обкладки конденсатора, заряжают разноименными зарядами, равными по абсолютной величине:
Емкость конденсатора:
9.11.1. Электроемкость плоского конденсатора
Из (9.11):
Энергия электрического поля
q+ = q- = q,
где
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.199.4 (0.011 с.) |

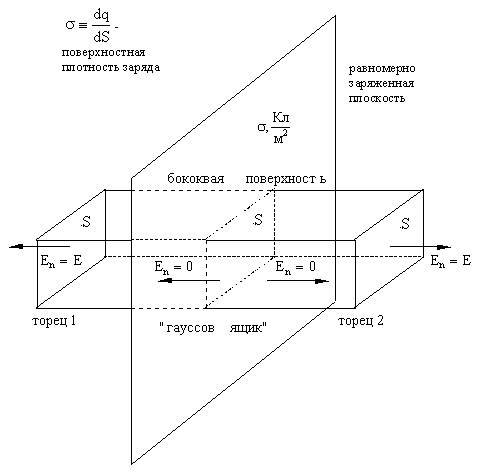
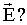 - только по нормали к плоскости! Значит, S надо выбрать так, чтобы вектор
- только по нормали к плоскости! Значит, S надо выбрать так, чтобы вектор  был либо параллелен ей (Еn=0), либо перпендикулярен (Еn=E).
был либо параллелен ей (Еn=0), либо перпендикулярен (Еn=E).
 ;
; .
.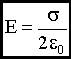 .
.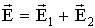 .
. 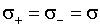 , то по 9.4.4.1
, то по 9.4.4.1  .
.


 - линейная плотность заряда.
- линейная плотность заряда. 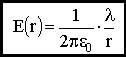 , при r > R.
, при r > R.
 при r > R. Если r < R, то E = 0.
при r > R. Если r < R, то E = 0.
 - объемная плотность заряда
- объемная плотность заряда 

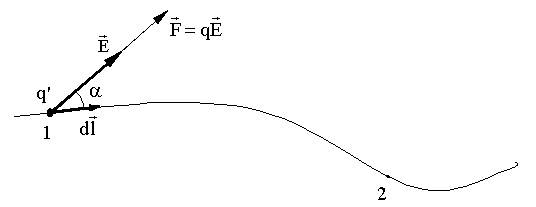
 из (9.3.5).
из (9.3.5). .
. ;
; ,
, .
.
 ,
,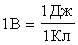 .
. . Из (9.6):
. Из (9.6):  ;
;  ;
; 

 .
. .
. .
. ,
,
 ,
, ;
;


 из точки 1 в точку 2.
из точки 1 в точку 2.  ,
, 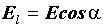 ;
; .
. .
. .
. .
.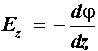 .
. .
. .
. - оператор набла.
- оператор набла.



 .
. .
. 
 (объем проводника эквипотенциален)
(объем проводника эквипотенциален)  - на поверхности, сама поверхность (9.7), (9.8) - эквипотенциальная.
- на поверхности, сама поверхность (9.7), (9.8) - эквипотенциальная.


 начинают двигаться против поля.
начинают двигаться против поля.

 .
.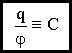
 .
. .
. .
.
 по (9.4.4.2):
по (9.4.4.2): 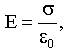 по (9.4.4.1):
по (9.4.4.1): 
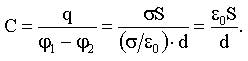

 .
.  (9.4.4.2).
(9.4.4.2). . См. (9.3.5)
. См. (9.3.5) в объеме ΔV исчезло, значит работа A12 совершена за счет убыли энергии поля:
в объеме ΔV исчезло, значит работа A12 совершена за счет убыли энергии поля: .
.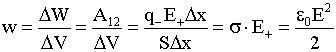 ,
,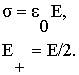 .
.


