
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одновременность событий в разных системах отсчетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В системе K' одновременно (в момент времени t'), нo в разных местах (x'1 и, x'2) произошли два события.
Время первого события в системе К:
второго
Видно, что t2> t1, т. к. x'2>x'1. В системе К события не одновременны. Промежуток времени между двумя событиями
Пусть в системе К' в одной и той же точке с координатой х' происходят в моменты времени t'1 и t'2 два события (например, две вспышки света). В этой системе промежуток времени между событиями: В системе К:
Т.к. γ всегда больше единицы, то Δt > Δt'. Длина тела в разных системах отсчета
Пусть стержень длины l0 лежит вдоль оси x' в системе К'. Как измерить его длину в системе К, относительно которой он движется? Мы, в системе К, должны в один и тот же момент времени t (по чаcам системы К) измерить координаты начала и конца стержня. Их разница и будет длиной движущегося стержня. Тогда:
8.6.4. Преобразование скоростей Пусть материальная точка движется в системе К со скоростью
Компоненты скорости материальной точки (3.8.2.):
Т.к.
То
Это формулы релятивистского преобразования скоростей, они дают связь между компонентами скорости частицы в различных системах отсчета: в системе K и в движущейся со скоростью V системе K'. Релятивистская динамика Релятивистский импульс В классической механике В релятивистской механике, где v → c,
Выражение для релятивистского импульса отличается от классического множителем γ. 8.7.2. Уравнение движения в релятивистской механике такое же, как и в классической (4.6)
Релятивистское выражение для энергии
Энергия покоя При скорости материальной точки v=0
Кинетическая энергия (энергия движения)
8.7.3.3. Релятивистский инвариант Из (8.7.3) и (8.7.1) следует, что
т.е. не зависит от выбора системы отсчета. Электричество
Постоянное электрическое поле Постоянный электрический ток Постоянное электрическое поле Электрический заряд Электрический заряд - определение Электрический заряд - характеристика частиц, определяющая интенсивность их электромагнитного взаимодействия. Два вида зарядов
Существует два вида электрических зарядов, условно называемых положительными и отрицательными. Взаимодействие зарядов разных знаков
Элементарные частицы - носители заряда Носителями заряда являются элементарные частицы, заряд элементарных частиц, если они заряжены, одинаков по абсолютной величине e = 1.6·10-19 Кл. 9.1.5. Электрон имеет отрицательный заряд (-е), протон - положительный (+е), заряд нейтрона равен нулю. Из этих частиц построены атомы любого вещества. Суммарный заряд атома равен нулю. 9.1.6. Закон сохранения заряда утверждает: В электрически изолированной системе суммарный заряд не может изменяться. 9.1.7. Релятивистская инвариантность заряда означает, что его величина, измеренная в различных инерциальных системах отсчета, оказывается одинаковой. Взаимодействие точечных зарядов 9.2.1. Точечный заряд - модель заряженного тела, сохраняющая три его свойства: положение в пространстве, заряд и массу. 9.2.2. Закон Кулона
ε0 = 8.85 ·10-12 Ф/м.
9.2.3. Единица заряда в системе СИ - кулон Один кулон (1 Кл) определяется через единицу силы тока, см. (10.1). 9.2.4. Принцип суперпозиции утверждает, что сила взаимодействия двух зарядов не изменится, если к ним добавить еще какие либо заряды. Для зарядов на рисунке это значит, что
Электрическое поле 9.3.1. Заряд - источник поля. Всякий покоящийся заряд создает в пространстве вокруг себя только электрическое поле. Движущийся - еще и магнитное. 9.3.2. Заряд - индикатор поля. О наличии электрического поля судят по силе, действующей на неподвижный положительный точечный заряд, помещенный в это поле (пробный заряд).
9.3.3. Напряженность - силовая характеристика электрического поля. Если на неподвижный точечный заряд qпр. действует сила, то значит, в точке нахождения этого заряда существует электрическое поле, напряженность которого определяется так:
9.3.4. Единица напряженности в системе СИ имеет название вольт на метр (В/м), при такой напряженности на заряд в 1 Кл действует сила в 1 Н. Происхождение размерности В/м см (9.7). 9.3.5. Знаем напряженность - найдем силу
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.190.254 (0.009 с.) |


 ,
, .
.

 .
. .
.
 ,
, .
.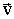 .
.  .
.
 ;
; ;
;  ;
;  .
. (4.5), при v << c.
(4.5), при v << c. .
. но
но 
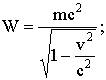

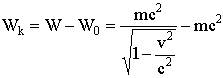 .
. - inv, инвариант,
- inv, инвариант,


 .
. ,
, .
. и
и  не зависят от присутствия заряда q3,
не зависят от присутствия заряда q3,  и
и  не зависят от присутствия заряда q2, аналогично -
не зависят от присутствия заряда q2, аналогично -  и
и  не завися от заряда q1.
не завися от заряда q1.
 ,
аналогично и для остальных зарядов:
,
аналогично и для остальных зарядов:


 .
.
 , то мы можем найти силу, действующую на точечный заряд, помещенный в точку r (9.3.3)
, то мы можем найти силу, действующую на точечный заряд, помещенный в точку r (9.3.3) .
.


