
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь плотности тока и скорости упорядоченного движения зарядовСодержание книги
Поиск на нашем сайте
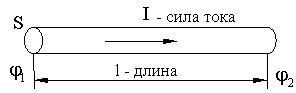
Сила тока:
Вектор 10.3. ЭДС источника
φ1 = φ2, если траектория замкнута.
где q - заряд, над которым сторонние силы совершили работу Aст.сил.
Единица ЭДС - такая же, как и единица потенциала - вольт. Закон Ома для участка цепи
R - сопротивление проводника.
ρ - удельное сопротивление (из таблиц).
Закон Ома в дифференциальной форме
Закон Ома (10.4) для элементарного объема проводника.
См. (9.7) Используя (10.2) получим:
Закон Джоуля-Ленца в дифференциальной форме
Количество тепла, выделяемое в элементарном объеме с сопротивлением R при прохождении тока I в течении времени dt:
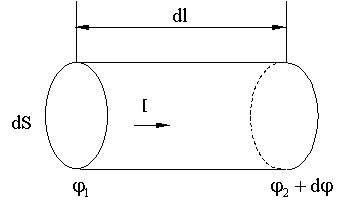
См. (10.2), (10.4), (10.5). Закон Ома для неоднородного участка цепи Неоднородный участок - участок, содержащий ЭДС.
dA12 переходит в джоулево тепло I2Rdt (10.6):
Закон Ома для неоднородного участка цепи:
Магнетизм. Уравнения Максвелла
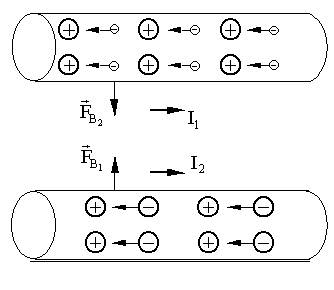
Магнитное поле в вакууме Магнитное поле в веществе Уравнения Максвелла Магнитное поле в вакууме Движущийся заряд - источник магнитного поля, индикатор магнитного поля - другой движущийся заряд
Проводник с током создает только магнитное поле, другой проводник с током реагирует только на магнитное поле
Рамка с током как регистратор магнитного поля. Вектор магнитной индукции
Вращающий момент (7.1)
11.3.1. Линии магнитной индукции: а) замкнуты, т.к. в природе нет магнитных зарядов; Закон Био-Савара-Лапласа
Модуль вектора
Применение закона Био-Савара-Лапласа для нахождения магнитного поля прямого тока
Независимо от положения
Для бесконечного проводника α1 = 0, α2 = π, Сos α1 - Сos α2 = 2
Теорема о циркуляции вектора В Циркуляция вектора В по произвольному контуру равна алгебраической сумме токов, охватываемых контуром, помноженной на μ0. 11.5.1. Циркуляция вектора
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |


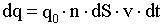 ,
где q0 - заряд одного носителя; n - число зарядов в единице объема; dS·v·dt - объем.
,
где q0 - заряд одного носителя; n - число зарядов в единице объема; dS·v·dt - объем.
 .
. .
.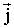 направлен как и вектор
направлен как и вектор 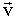 .
. .
. .
. .
.
 ,
,
 .
. ,
, .
.

 ,
,
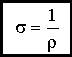 .
.





 ,
где dq(φ1-φ2) - работа сил поля (9.6.2), dq ε12 - работа сторонних сил (10.3).
,
где dq(φ1-φ2) - работа сил поля (9.6.2), dq ε12 - работа сторонних сил (10.3).
 ,
, (10.1),
(10.1), .
. .
.

 ,
и магнитное поле с индукцией
,
и магнитное поле с индукцией 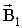 . На заряд q2 действуют две силы:
. На заряд q2 действуют две силы:  - электрическая, см. (9.3.5),
- электрическая, см. (9.3.5),  - магнитная сила, или сила Лоренца, см. (11.7). Если q2 неподвижен, на него действует ТОЛЬКО
- магнитная сила, или сила Лоренца, см. (11.7). Если q2 неподвижен, на него действует ТОЛЬКО  .
.

 .
. 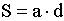
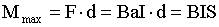 .
.  совпадает с направлением положительной нормали
совпадает с направлением положительной нормали  к рамке.
к рамке. 

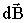
 плоскости, в которой лежит
плоскости, в которой лежит  и
и  и определяется правилом правого винта:
и определяется правилом правого винта: 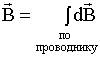
 .
.
 - без векторов!
- без векторов! 

 .
.
 Интеграл берется по замкнутому контуру.
Интеграл берется по замкнутому контуру.



