
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предсказание будущего - задача наукиСтр 1 из 12Следующая ⇒
Вводные сведения Предсказание будущего - задача науки Зачем естественные науки нужны людям? Одно из основных назначений наук о природе - предсказывать будущее состояние (поведение) изучаемых объектов. Предмет физики В чем состоит специфика физики, как одной из естественных наук, каков предмет физики? Физика - наука о наиболее простых общих свойствах окружающего нас мира. Физическая модель Как выделяют физики из бесконечного многообразия окружающего мира интересующие их немногочисленные простые свойства? Что такое физическая модель?
исследователь Модель какой-либо реальной системы - это другая система, в которой сохранены только существенные для рассматриваемой задачи свойства реальной системы и которую можно описать на языке данной науки. Модель какой-либо области явлений - это научная теория, изучающая эти явления. Физика строит модели действительного мира, которые может описать язык физики. Язык физики? На каком языке "говорит" физика? Язык физики количественный, точный. Он широко использует математику, иногда говорят: "Математика - язык физики". Предсказания (1.1) физических теорий - это точные, количественные предсказания. Экспериментальная и теоретическая физика Экспериментальная физика - это опыты, проводимые для: а) обнаружения новых фактов; б) проверки истинности предсказаний теории. Теоретическая физика формулирует физические законы, на основе которых объясняются обнаруженные на опыте факты и делаются предсказания новых явлений. Если предсказания теории подтверждаются большой совокупностью опытов, то теорию считают верной. Если на опыте не подтверждается хотя бы одно из предсказаний теории, то такую теорию необходимо либо изменить, либо заменить другой, более удовлетворительной. Старая теория в этом случае обычно не отбрасывается, но ее область применения уточняется и ограничивается.
Физические основы механики
Классическая механика, релятивистская механика, квантовая механика Элементы кинематики Динамика материальной точки Законы сохранения Кинематика вращательного движения Динамика вращательного движения
Элементы специальной теории относительности Классическая механика, релятивистская механика, квантовая механика Классическая механика Классическая механика справедлива для любых тел, кроме элементарных частиц. Скорости движения тел должны быть малы по сравнению со скоростью света, c = 3·108 м/с. В основе классической механики лежат законы Ньютона. Релятивистская механика Релятивистская механика, или специальная теория относительности. Согласно специальной теории относительности скорости тел не могут превышать скорость света. Релятивистская механика справедлива и при скоростях, сравнимых со скоростью света. Квантовая механика Квантовая механика изучает движение элементарных частиц. Элементы квантовой механики будут рассмотрены в третьей части конспекта. Предмет классической механики, ее основная задача Предмет механики Механика изучает изменение с течением времени взаимного положения материальных тел в пространстве и происходящие при этом взаимодействия между ними. Кинематика Кинематика - раздел механики, изучающий движения тел в пространстве и времени без рассмотрения вызывающих это движение взаимодействий. Динамика Динамика изучает движение тел учитывая взаимодействия между телами, которые обуславливают тот или иной характер движения. Статика Статика изучает законы равновесия системы тел. Эти законы следуют из законов динамики. Основная задача механики Основная задача механики - предсказывать будущее положение тел.
Элементы кинематики Материальная точка, система материальных точек, абсолютно твердое тело - простейшие физические модели Материальная точка Материальная точка - это одна из простейших физических моделей (1.3).
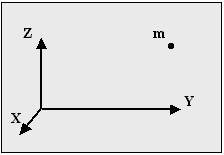
Тело из реального мира (см. рис.) иногда можно без ущерба для решаемой задачи заменить точкой в модельном мире, сохранив из всех многообразных свойств этого тела лишь два: положение в пространстве и массу. Эти две характеристики легко описать языком физики (1.4). Массу задают числом. Положение - координатами в выбранной системе координат (3.4.1).
Традиционное определение материальной точки: это тело, размерами которого можно пренебречь при описании его движения. Здесь вместе присутствуют понятия, описывающие и реальный мир, и модельный мир. 3.1.2. Система материальных точек Пример:
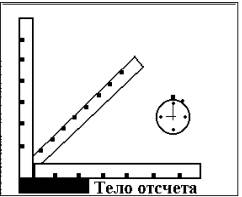
Абсолютно твердое тело Существуют такие задачи, в которых размерами тела нельзя пренебречь, но, в то же время, можно не учитывать изменение со временем размеров, формы тела. При решении таких задач используют модель - абсолютно твердое тело, т.е. реальное тело заменяют таким, у которого размеры и форма не меняются. Тело отсчета Тело отсчета - это тело, относительно которого определяют положение рассматриваемого нами тела или системы тел. Система отсчета Это система координат, связанная с телом отсчета (3.2) и выбранный способ измерения времени (часы).
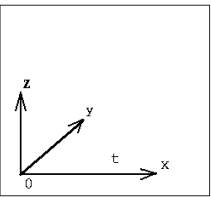
В реальном трехмерном мире система отсчета - это набор масштабных стержней (или линеек) и часы, расположенные в разных местах этих линеек. В модельном мире система отсчета превращается в трехмерную систему координат, положение которой связано с положением тела отсчета. В каждой точке пространства существует возможность определить время любого происшедшего в этой точке события. Координаты точки Первый способ задать положение материальной точки - это задать ее координаты. Например, три числа xА, yА, zА задают положение точки A в декартовой системе координат.
Компоненты радиус-вектора На плоскости:
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются координатами материальной точки. Модуль радиус-вектора
3.6. Путь - длина отрезка траектории (3.5). 3.7. Перемещение - вектор, проведенный из начального положения (3.4.1), (3.4.2) материальной точки (3.1.1) в ее конечное положение.
Компоненты скорости На следующем рисунке изображен вектор скорости
Так как С другой стороны: откуда т.е. компоненты скорости равны производным соответствующих координат по времени. 3.8.3. Модуль скорости - производная пути по времени.
По теореме Пифагора: Вычисление пройденного пути Для равномерного движения
Для произвольного движения:
v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
т.е. путь - это определенный интеграл от модуля скорости по времени. 3.10. Ускорение - это производная скорости по времени.
Учитывая (3.8), получим:
Ускорение - вторая производная радиуса-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение - это скорость изменения скорости. Динамика материальной точки 4.1. Почему в кинематике вводят только две производные от радиус-вектора:
А если ввести некую Можно, но обычно не нужно. Основная задача механики - предсказать положения тел в любой момент времени, т.е. предсказать вид функции Закон обнаруживается на более глубоком уровне - на уровне второй производной от радиус - вектора:
Двигаясь по этой цепочке "обратным ходом", мы можем, получив из закона природы (второй закон Ньютона) ускорение Размерность силы
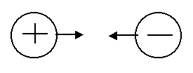
1 ньютон (1Н) - это сила, которая массе 1 кг сообщает ускорение 1 м/с. 4.7. Третий закон Ньютона Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример - взаимодействие двух электрических зарядов:
Законы сохранения Внутренние и внешние силы
5.1.2. Замкнутая система
5.1.3. Импульс системы материальных точек - это векторная сумма импульсов всех материальных точек, входящих в систему
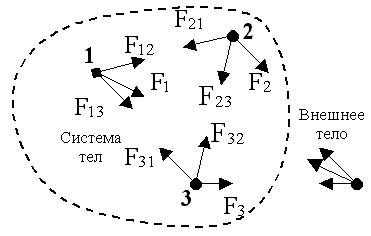
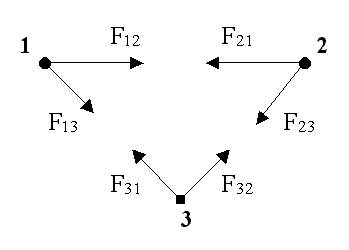
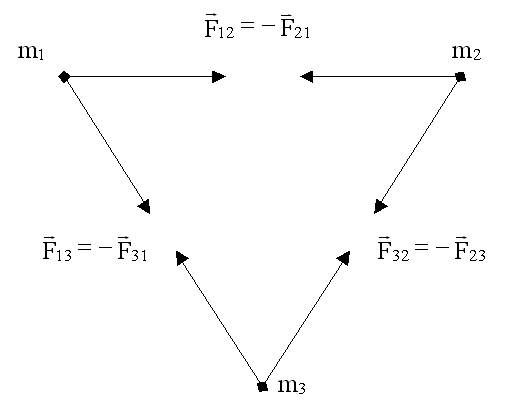
Закон сохранения импульса Импульс замкнутой системы сохраняется, т.е. не изменяется со временем. На рисунке изображена замкнутая система, состоящая из трех тел.
По II закону Ньютона (4.6), примененному к каждому телу рассматриваемой замкнутой системы, имеем:
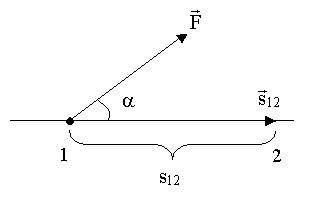
Работа Работа постоянной силы
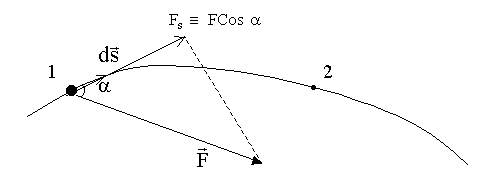
Элементарная работа
Работа переменной силы
Единица измерения работы [A]=[F].[s]= H.м = джоуль, Дж 5.4. Мощность P - это скорость совершения работы, т.е.
Единица мощности
Кинетическая энергия
Используя (5.3.2) справа и преобразуя левую часть,
получим
Половина произведения массы частицы на квадрат ее скорости названа ее кинетической энергией
Таким образом элементарная работа, совершаемая над телом, равна элементарному приращению его кинетической энергии. При интегрировании вдоль траектории частицы, от точки 1 до точки 2, мы получим:
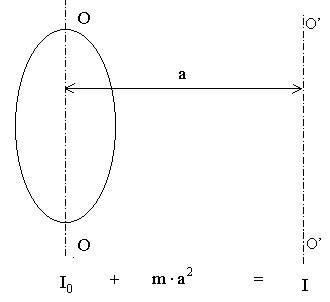
Работа результирующей силы идет на приращение кинетической энергии материальной точки. 5.6. Консервативные и неконсервативные силы Теорема Штейнера
где I0 - момент инерции относительно оси OО, 7.2.2. Моменты инерции I0 для некоторых тел
Постулаты С.Т.О. Механика больших скоростей, специальная теория относительности (С.Т.О.), базируется на двух исходных утверждениях, постулатах: I. Принцип относительности, согласно которому Релятивистская динамика Релятивистский импульс В классической механике В релятивистской механике, где v → c,
Выражение для релятивистского импульса отличается от классического множителем γ. 8.7.2. Уравнение движения в релятивистской механике такое же, как и в классической (4.6)
Энергия покоя При скорости материальной точки v=0
Электричество
Электрический заряд
Два вида зарядов Существует два вида электрических зарядов, условно называемых положительными и отрицательными. Электрическое поле 9.3.1. Заряд - источник поля. Всякий покоящийся заряд создает в пространстве вокруг себя только электрическое поле. Движущийся - еще и магнитное. 9.3.2. Заряд - индикатор поля. О наличии электрического поля судят по силе, действующей на неподвижный положительный точечный заряд, помещенный в это поле (пробный заряд). 9.3.3. Напряженность - силовая характеристика электрического поля. Если на неподвижный точечный заряд qпр. действует сила, то значит, в точке нахождения этого заряда существует электрическое поле, напряженность которого определяется так:
9.3.4. Единица напряженности в системе СИ имеет название вольт на метр (В/м), при такой напряженности на заряд в 1 Кл действует сила в 1 Н. Происхождение размерности В/м см (9.7). 9.3.5. Знаем напряженность - найдем силу
Линии напряженности Для графического изображения электрического поля используются линии напряженности (силовые линии). Их строят по следующим правилам:
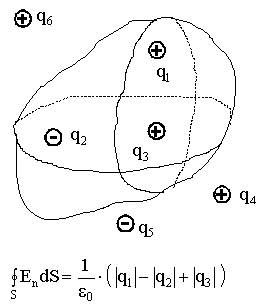
Теорема Гаусса Формулировка теоремы Гаусса
Из (9.4.1.3)
9.4.4. Применение теоремы Гаусса для вычисления полей.
S - любая замкнутая поверхность, а) САМИ выбрать конкретную гауссову поверхность S, такую, чтобы интеграл по этой поверхности легко считался. Затем найти б) посчитать сумму зарядов внутри выбранной нами S; в) приравнять результат полученный в пункте а), к результату, полученному в пункте б), деленному на ε0. Поле плоского конденсатора По 9.3.6.
Единица потенциала - 1 вольт (1 В)
Электроемкость конденсатора Конденсатор - это два проводника, обычно плоской цилиндрической или сферической формы, расположенные на небольшом расстоянии друг от друга. Проводники, обкладки конденсатора, заряжают разноименными зарядами, равными по абсолютной величине:
Емкость конденсатора:
9.11.1. Электроемкость плоского конденсатора
Из (9.11):
Энергия электрического поля
q+ = q- = q,
где
Диэлектрик? Заряды, входящие в состав молекул диэлектрика, прочно связаны друг с другом и под действием внешнего поля могут лишь немного смещаться в противоположные стороны. Сила тока
За время dt переносится заряд dq.
Единица силы тока - ампер. Плотность тока
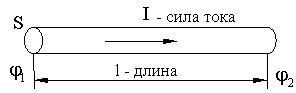
Закон Ома для участка цепи
R - сопротивление проводника.
ρ - удельное сопротивление (из таблиц).
Магнитное поле в вакууме Магнитное поле в веществе Уравнения Максвелла Магнитное поле в вакууме Закон Био-Савара-Лапласа
Модуль вектора
Ток за контуром
11.5.4. Формулировка теоремы о циркуляции
Например:
Ток I4 в сумму не входит! 11.5.5. Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида
Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор
1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1
3) Можно показать, что вне бесконечного соленоида B=0, т.е.
Значит:
т.к. внутри соленоида B = Bl = const, то
По теореме о циркуляции (11.5.4)
Откуда магнитное поле бесконечного соленоида:
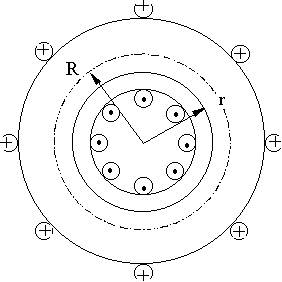
Направлено Магнитное поле тороида
Магнитное поле тороида:
Вне тора поле Закон Ампера
Вектор вращающего момента
Магнитный момент по полю
Контур разворачивается так, чтобы 11.8.2.3. Сила, действующая на контур при произвольной ориентации Эта сила направлена по оси симметрии поля z и равна:
11.9. Поток вектора магнитной индукции (магнитный поток) 11.9.1. Для однородного
11.9.2. Поток вектора
11.9.3. Поток вектора
11.10. Явление электромагнитной индукции состоит в том, что любое изменение магнитного потока Ф, пронизывающего замкнутый контур, вызывает появление индукционного тока в контуре.
Закон Фарадея - Ленца Закон Фарадея-Ленца утверждает, что ЭДС индукции равна скорости изменения магнитного потока, взятой с обратным знаком.
Знак минус напоминает о правиле Ленца: индукционный ток имеет такое направление, чтобы создаваемое им магнитное поле препятствовало изменению магнитного потока. Потокосцепление
Сопоставляя с выражением εсам через ψ, получим:
Индуктивность соленоида
Число витков на единицу длины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.265 с.) |















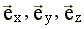 - единичные векторы или орты, направленные по осям x, y, z соответственно;
- единичные векторы или орты, направленные по осям x, y, z соответственно; - по теореме Пифагора.
- по теореме Пифагора.
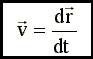 либо, применяя другое обозначение производной по времени,
либо, применяя другое обозначение производной по времени, 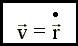
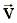 материальной точки M, движущейся по плоскости x, y:
материальной точки M, движущейся по плоскости x, y:
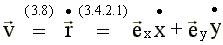 .
. ,
, , так же и
, так же и  ,
, .
. .
. ,
,  - весь путь,
- весь путь,  - весь отрезок времени,
- весь отрезок времени,  - const.
- const.
 .
.
 ,
, или
или 
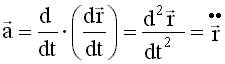
 .
. .
. ?
? для всех изучаемых тел. Но в природе не существует фундаментального закона, что-либо утверждающего непосредственно о радиус-векторе материальной точки.
для всех изучаемых тел. Но в природе не существует фундаментального закона, что-либо утверждающего непосредственно о радиус-векторе материальной точки. - нет закона;
- нет закона;  - нет закона;
- нет закона;  - есть закон! →
- есть закон! → 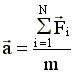 , см. (4.6).
, см. (4.6). , найти сначала
, найти сначала 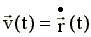 , затем и
, затем и  больше, чем два раза.
больше, чем два раза.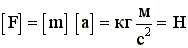 ,
,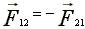
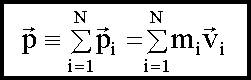 , (см. 4.5).
, (см. 4.5).
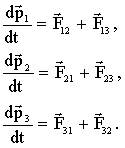
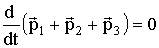
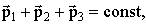
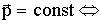


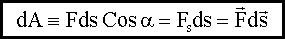
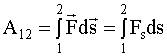
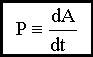
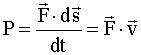
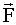 .
.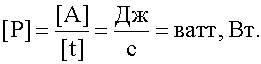

 :
:

 - справа на
- справа на 
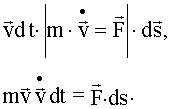 .
.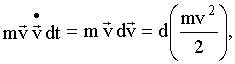
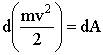 .
.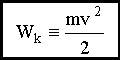
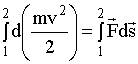

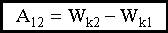
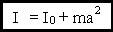 ,
,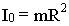 ,
,
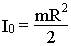 ,
,
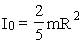 ,
,
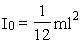 ,
,
 (4.5), при v << c.
(4.5), при v << c. .
. но
но 



 .
.
 , то мы можем найти силу, действующую на точечный заряд, помещенный в точку r (9.3.3)
, то мы можем найти силу, действующую на точечный заряд, помещенный в точку r (9.3.3) .
.

 , тогда теорема Гаусса запишется так:
, тогда теорема Гаусса запишется так:

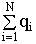 - сумма зарядов внутри S.
- сумма зарядов внутри S.  ;
;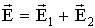 .
. 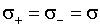 , то по 9.4.4.1
, то по 9.4.4.1  .
.

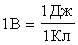 .
. .
. .
.
 по (9.4.4.2):
по (9.4.4.2): 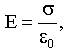 по (9.4.4.1):
по (9.4.4.1): 
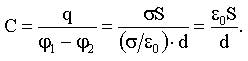

 .
.  (9.4.4.2).
(9.4.4.2). . См. (9.3.5)
. См. (9.3.5) в объеме ΔV исчезло, значит работа A12 совершена за счет убыли энергии поля:
в объеме ΔV исчезло, значит работа A12 совершена за счет убыли энергии поля: .
.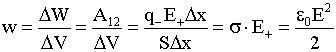 ,
,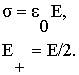 .
.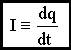 .
.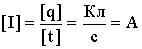 .
.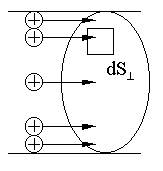
 , dI - сила тока, проходящего через площадку dS1.
, dI - сила тока, проходящего через площадку dS1.
 ,
,
 .
. ,
, .
.
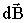
 плоскости, в которой лежит
плоскости, в которой лежит  и
и  и определяется правилом правого винта:
и определяется правилом правого винта: 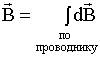
 .
.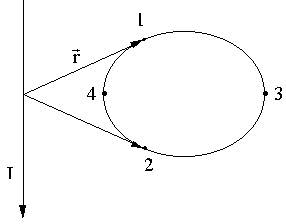

 по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е. .
.
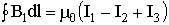

 .
. .
. .
. ,
, .
. .
.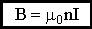 .
.
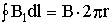 .
По теореме о циркуляции:
.
По теореме о циркуляции:
 ,
,  , R - радиус тора.
, R - радиус тора.
 .
.
 , которая определяется следующим образом. Направлен вектор
, которая определяется следующим образом. Направлен вектор 
 При параллельности
При параллельности  и
и 
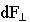 и силы
и силы 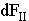 , втягивающие контур в область более сильного поля.
, втягивающие контур в область более сильного поля.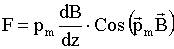






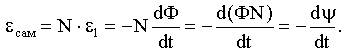 Величину ψ назвали потокосцеплением:
Величину ψ назвали потокосцеплением:
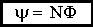 .
.
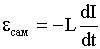 .
. .
.
 .
. (11.9.1);
(11.9.1);


