
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Консервативность силы тяжестиСодержание книги
Поиск на нашем сайте
Неконсервативность силы трения
Потенциальная энергия может быть введена только для поля консервативных сил Так как их работа не зависит от траектории, а только от начального и конечного положений материальной точки, то эту работу можно записать в виде разности двух чисел: одно - Wn1 - будет зависеть от начального положения тела, второе - Wn2 - от конечного положения тела.
5.7.1. Некоторые конкретные выражения для потенциальной энергии Wn(r)
В частности, для однородного поля тяжести, где Если Если Закон сохранения механической энергии Для одной материальной точки, движущейся в поле консервативных сил, из (5.5) A12 = Wk2 - Wk1, из (5.7) A12 = Wn1 - Wn2. Откуда Wn1 - Wn2 = Wk2 - Wk1 или Wk1 + Wn1 = Wk2 + Wn2. В поле консервативных сил сумма кинетической и потенциальной энергии материальной точки остается постоянной, т.е. сохраняется.
5.8.2. Полная энергия системы материальных точек
5.8.2.1. Закон сохранения энергии для системы материальных точек
где W'п - потенциальная энергия системы во внешнем поле.
Кинематика вращательного движения Поступательное и вращательное движение
а) поступательное движение. Любая линия, проведенная в твердом теле, при движении остается параллельной самой себе.
б) вращательное движение, центр масс движется по окружности того же радиуса. Каждая точка твердого тела движется по своей окружности; центры всех окружностей лежат на прямой, называемой осью вращения. Псевдовектор бесконечно малого поворота
6.3. Угловая скорость, сравните с (3.8).
Связь линейной скорости материальной точки твердого тела и угловой скорости
6.6. Связь линейного ускорения материальной точки твердого тела с угловой скоростью и угловым ускорением
Из (3.10.1)
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.3 (0.008 с.) |


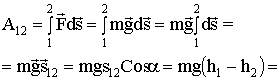

 вектор перемещения,
вектор перемещения, .
.
 cosα = -1.
cosα = -1.

 .
. .
. .
. , используя (5.6.1), получим: Wn = mgh.
, используя (5.6.1), получим: Wn = mgh. 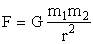 - гравитационная сила, то
- гравитационная сила, то 
 - кулоновская сила, то
- кулоновская сила, то  .
. - сила упругости, то
- сила упругости, то  .
. - полная энергия материальной точки.
- полная энергия материальной точки. ,
, ,
,

 . В правой системе координат направление
. В правой системе координат направление 
 , или
, или 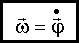 . Псевдовектор
. Псевдовектор  направлен так же, как и псевдовектор
направлен так же, как и псевдовектор 

 откуда
откуда
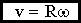
 ,
,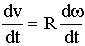 ,
,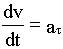 , используя (6.4)
, используя (6.4) .
.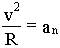 , заменяя
, заменяя 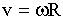 , (6.5), получим
, (6.5), получим .
.


