
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип суперпозиции электрических полей
Напряженность поля точечного заряда
а) поместим в точку
!!! Пробный заряд в ответ не входит!
Линии напряженности Для графического изображения электрического поля используются линии напряженности (силовые линии). Их строят по следующим правилам:
Линии напряженности точечных зарядов
Теорема Гаусса Поток вектора напряжeнности электрического поля 9.4.1.1. - Поток вектора Для
9.4.1.2. Поток вектора
9.4.1.3. Поток вектора
9.4.1.4. Поток пропорционален числу силовых линий 9.4.2. Поток вектора 9.4.2.1. Заряд - в центре сферы
В любой точке сферы поле направлено перпендикулярно ее поверхности, т.е.
Мы получили, что:
Заряд в произвольном месте внутри сферы
Поток Ф пропорционален числу силовых линий, проходящих через сферу, а их число не изменяется при изменении положения заряда внутри сферы, т.е. поток тоже будет постоянным:
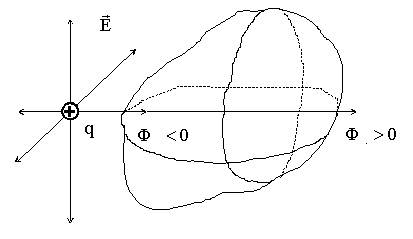
9.4.2.3. Поток вектора Е поля точечного заряда через "измятую" сферу - произвольную поверхность
Эта формула верна для потока вектора Е поля точечного заряда, расположенного ВНУТРИ замкнутой поверхности произвольной формы.
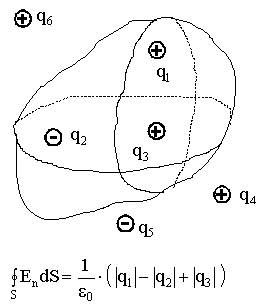
Поток вектора Е поля системы зарядов, находящихся внутри замкнутой поверхности
Поток вектора Е для поля, созданного зарядами, находящимися вне замкнутой поверхности
Формулировка теоремы Гаусса
Из (9.4.1.3)
9.4.4. Применение теоремы Гаусса для вычисления полей.
S - любая замкнутая поверхность, а) САМИ выбрать конкретную гауссову поверхность S, такую, чтобы интеграл по этой поверхности легко считался. Затем найти б) посчитать сумму зарядов внутри выбранной нами S; в) приравнять результат полученный в пункте а), к результату, полученному в пункте б), деленному на ε0.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.221.113 (0.007 с.) |

 .
.

 точечным зарядом q.
точечным зарядом q.
 пробный заряд qпр и найдем по закону Кулона (9.2.2) силу,
пробный заряд qпр и найдем по закону Кулона (9.2.2) силу,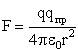 ;
; .
. .
. .
. а) поле положительного заряда
а) поле положительного заряда
 в) поле двух разноименных зарядов
в) поле двух разноименных зарядов
 г) поле двух одноименных зарядов
г) поле двух одноименных зарядов
 для однородного поля
для однородного поля


 - вектор нормали к поверхности S.
- вектор нормали к поверхности S.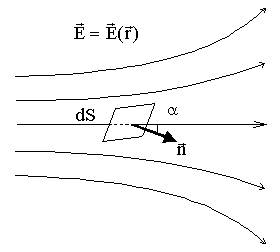
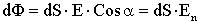
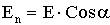

 .
. .
.
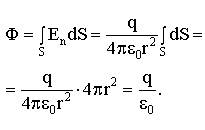
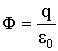 .
. .
.
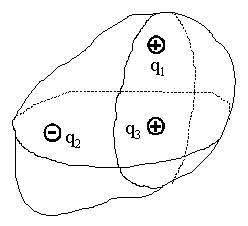
 (9.3.6), то по (9.4.1.3) и (9.4.2.3)
(9.3.6), то по (9.4.1.3) и (9.4.2.3)
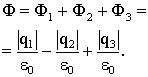 Для произвольного числа зарядов N:
Для произвольного числа зарядов N:  - алгебраическая сумма зарядов, находящихся внутри замкнутой поверхности, делённая на ε0.
- алгебраическая сумма зарядов, находящихся внутри замкнутой поверхности, делённая на ε0.

 , тогда теорема Гаусса запишется так:
, тогда теорема Гаусса запишется так:

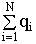 - сумма зарядов внутри S.
- сумма зарядов внутри S.  ;
;


