
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электронный механизм ЭДС индукции⇐ ПредыдущаяСтр 12 из 12
На рисунке изображена рамка с подвижной стороной. Магнитное поле
перемещающая заряд на расстояние l и совершающая работу (5.3.1):
ЭДС ε (10.3):
Найдем e по закону Фарадея (11.10.1):
Подвижная сторона рамки "заметает" за время dt площадь dS = lvdt, тогда
Результат тот же, значит: Электронный механизм возникновения ЭДС индукции - это работа компоненты силы Лоренца. 11.10.2.1. Вихревое электрическое поле
В этой системе отсчета v = 0,
Источником этого электрического поля является не заряд, как в статическом случае (9.3.1), а движущееся магнитное поле. Такое электрическое поле называют вихревым, т. к. его линии напряженности замкнуты. Работа вихревого поля по перемещению заряда по замкнутому контуру не равна нулю (в отличии от электростатического поля). 11.11. Самоиндукция
Можно записать связь между потоком и током:
здесь L - индуктивность контура, [L] = Гн (генри).
если L = const, то
Потокосцепление
Сопоставляя с выражением εсам через ψ, получим:
Индуктивность соленоида
Число витков на единицу длины
См. (11.11.1), (11.5.5)
Энергия магнитного поля
Работа эта совершена за счет исчезновения магнитного поля соленоида (11.5.5).
Плотность энергии магнитного поля В единице объема магнитного поля запасена энергия:
Магнитное поле в веществе 12.1. Магнитная проницаемость - это отношение магнитной индукции B в веществе к магнитной индукции в вакууме B0.
Классификация магнетиков
12.3. Диамагнетики - по закону Фарадея-Ленца (11.10.1) при внесении в магнитное поле
12.4. Парамагнетизм проявляется у веществ, атомы которых имеют собственный магнитный момент. Магнитные моменты
12.5. Ферромагнетизм - объясняется самопроизвольным упорядочением спиновых магнитных моментов электронов в пределах областей спонтанного намагничивания (доменов).
Уравнения Максвелла
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.015 с.) |
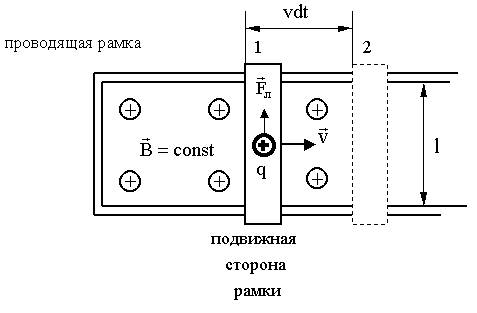
 направлено от нас.
направлено от нас.  . На заряд +q действует сила Лоренца
. На заряд +q действует сила Лоренца ,
, .
. .
. .
. .
.
 , но магнитное поле движется со скоростью
, но магнитное поле движется со скоростью  .
.  , значит, эта сила действует со стороны ЭЛЕКТРИЧЕСКОГО ПОЛЯ напряженностью (9.3.3.):
, значит, эта сила действует со стороны ЭЛЕКТРИЧЕСКОГО ПОЛЯ напряженностью (9.3.3.): .
.
 ,
, ,
, .
.
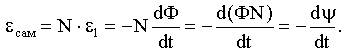 Величину ψ назвали потокосцеплением:
Величину ψ назвали потокосцеплением:
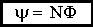 .
.
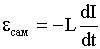 .
. .
.
 .
. (11.9.1);
(11.9.1); .
.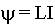 , см. (11.11.1), следовательно:
, см. (11.11.1), следовательно: .
.
 .
См. (10.3), (10.1), (11.11.1).
.
См. (10.3), (10.1), (11.11.1).
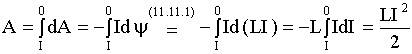 .
. .
. .
. .
. ,
,
 при T ≈ 300 K,
при T ≈ 300 K,
 для Fe, при T ≈ 300 K, при
для Fe, при T ≈ 300 K, при 
 любого вещества в атомах вещества возникают внутренние токи, создающие магнитное поле
любого вещества в атомах вещества возникают внутренние токи, создающие магнитное поле  , направленное навстречу внешнему полю
, направленное навстречу внешнему полю 
 атомов выстраиваются по полю
атомов выстраиваются по полю 






 называется вектором напряженности магнитного поля. Он носит вспомогательный характер, силовой характеристикой магнитного поля является вектор магнитной индукции
называется вектором напряженности магнитного поля. Он носит вспомогательный характер, силовой характеристикой магнитного поля является вектор магнитной индукции  .
. - (9.3.3), (11.10.2.1);
- (9.3.3), (11.10.2.1); - (9.13.4);
- (9.13.4); 


