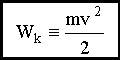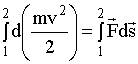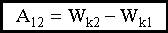Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерциальные системы отсчета. Первый закон НьютонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Инерциальная система отсчета - это система отсчета (3.3), в которой тела, Первый закон Ньютона: Всякое тело находится в состоянии покоя или равномерного прямолинейного 4.3. Сила 4.4. Масса тела, m, - скалярная величина, являющаяся мерой инертности тела. Инертность - неподатливость действию силы, свойство тела сохранять величину и направление своей скорости, невозможность ее мгновенного изменения. 4.5. Импульс материальной точки - это вектор, равный, в механике Ньютона, произведению массы точки на ее скорость.
При v → с это определение импульса не годится. Импульс в этом случае (в теории относительности):
4.6. Второй закон Ньютона Скорость изменения импульса равна действующей на материальную точку результирующей силе:.
Из (4.5)
при m ≠ m(t)
т.к.
Система СИ (System international) В этой системе семь основных единиц, для них существуют эталоны. Это единица длины - метр (м); массы - килограмм (кг); времени - секунда (с); силы электрического тока - ампер (А); температуры - Кельвин (К); силы света - кандела (кд); количества вещества - моль (моль). Все остальные единицы являются производными, их размерности определяются из формул, связывающих производные величины с основными. В механике используются первые три единицы: метр, килограмм, секунда. Отметим, что с точки зрения логики эти три единицы являются достаточными для введения производных от них величин не только в механике, но и во всей физике. Размерность силы
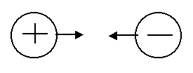
1 ньютон (1Н) - это сила, которая массе 1 кг сообщает ускорение 1 м/с. 4.7. Третий закон Ньютона Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример - взаимодействие двух электрических зарядов:
Законы сохранения Механическая система - это совокупность тел, выделенных нами для рассмотрения Внутренние и внешние силы
5.1.2. Замкнутая система
5.1.3. Импульс системы материальных точек - это векторная сумма импульсов всех материальных точек, входящих в систему
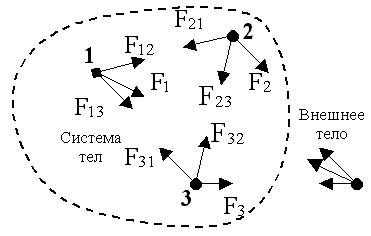
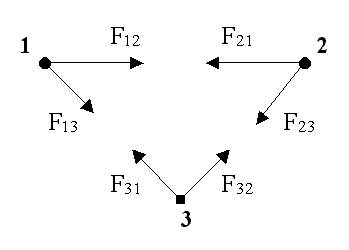
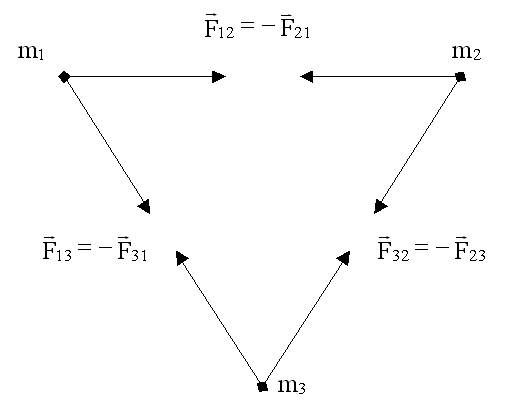
Закон сохранения импульса Импульс замкнутой системы сохраняется, т.е. не изменяется со временем. На рисунке изображена замкнутая система, состоящая из трех тел.
По II закону Ньютона (4.6), примененному к каждому телу рассматриваемой замкнутой системы, имеем:
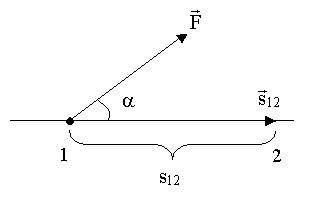
Работа Работа постоянной силы
Элементарная работа
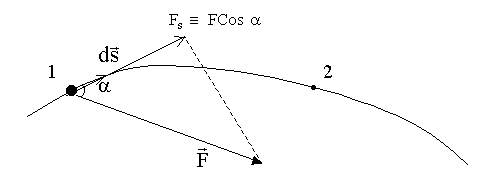
Работа переменной силы
Единица измерения работы [A]=[F].[s]= H.м = джоуль, Дж 5.4. Мощность P - это скорость совершения работы, т.е.
Единица мощности
Кинетическая энергия
Используя (5.3.2) справа и преобразуя левую часть,
получим
Половина произведения массы частицы на квадрат ее скорости названа ее кинетической энергией
Таким образом элементарная работа, совершаемая над телом, равна элементарному приращению его кинетической энергии. При интегрировании вдоль траектории частицы, от точки 1 до точки 2, мы получим:
Работа результирующей силы идет на приращение кинетической энергии материальной точки. 5.6. Консервативные и неконсервативные силы
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

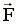 - векторная величина, характеризующая воздействие на данное тело других тел. Величину силы можно определить опытным путем, используя прибор для измерения силы - динамометр.
- векторная величина, характеризующая воздействие на данное тело других тел. Величину силы можно определить опытным путем, используя прибор для измерения силы - динамометр.
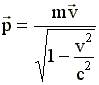 .
.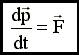 , где
, где 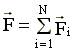

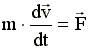 ,
, (3.10), то
(3.10), то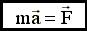 или
или 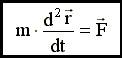 .
.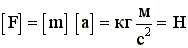 ,
,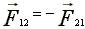
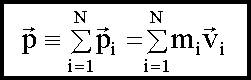 , (см. 4.5).
, (см. 4.5).
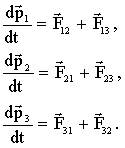
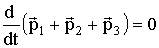
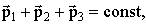
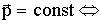


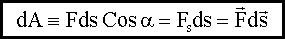
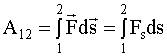
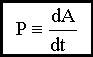
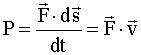
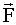 .
.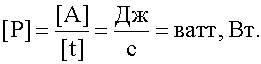

 :
:

 - справа на
- справа на 
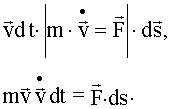 .
.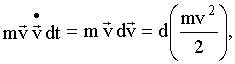
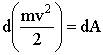 .
.