
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения импульса. Третий закон Ньютона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос№1 Мгновенной скоростью называется отношение изменения координаты точки к интервалу времени, за которое это изменение произошло, при интервале времени, стремящемся к нулю Средняя скорость - это весь путь разделить на затраченное время 1) Координатный способ: Если с системой отсчета связать декартову систему координат (X, Y, Z), то положение материальной точки А можно задать с помощью координат (x, y, z). Траекторию движения мы определим, если будем знать функцию x (t), y (t), z (t). Вопрос №2 Векторный и координатный способ описания движения точки впространстве. 1) Координатный способ:
Скорость-— векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. Ускорение-— физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной,показывающей, на сколько изменяется вектор скорости Вопрос №3 Баллистическое движение – движение тела в пространстве под действием внешних сил. Для примера рассмотрим движение тел под действием силы тяжести. Самый простой случай движения тел под действием силы тяжести – свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если начальная скорость тела отлична от нуля и вектор начальной скорости направлен не по вертикали, то тело под действием силы тяжести движется с ускорением свободного падения по криволинейной траектории (параболе).
Равномерное движение материальной ТОЧКИ по ОКРУЖНОСТИ ---
где Эта же формула определяет угол поворота абсолютно твёрдого тела при его равномерном вращении вокруг неподвижной оси, то есть при вращении с постоянной угловой скоростью Важной характеристикой данного типа движения является линейная скорость материальной точки Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения). Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению. Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Вопрос №4 Инерция — свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствии или при взаимной компенсации внешнихвоздействий. З-н инерции: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакиесилы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). (система Коперника) Гелиоцентрическая система мира — представление о том, что Солнце является центральным небесным телом, вокруг которого обращается Земля и другие планеты. Противоположность геоцентрической системе мира. Возникло вантичности, но получило широкое распространение с конца эпохи Возрождения. В этой системе Земля предполагается обращающейся вокруг Солнца за один звёздный год и вокруг своей оси за однизвёздные сутки. Следствием второго движения является видимое вращение небесной сферы, первого — перемещение Солнца среди звёзд по эклиптике. Солнце считается неподвижным относительно звёзд. Второй з-н Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этогоускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). Формулировка: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. Третий з-н Ньютона Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой Формулировка: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Область применимости третьего закона Ньютона. Всегда ли справедлив третий закон Ньютона в формулировке равенства действия и противодействия? Оказывается, что нет. Третий закон Ньютона при рассмотрении взаимодействия движущихся физических удаленных объектов носит приближенный характер. Это обусловлено конечным, а не мгновенным распространением взаимодействия (сила уже изменилась, но результат ее воздействия, а следовательно, и характер движения частицы еще нет). При непосредственном контактном взаимодействии третий закон Ньютона выполняется строго.
Вопрос № 5 Теорема о движении центра масс Теоре́ма о движе́нии це́нтра масс (це́нтра ине́рции) системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорениецентра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему Формулировка: Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.
Вопрос №6 Теорема Кёнига Теоре́ма Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс. Формулировка Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
где Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс. Связь сработой сил Кинетическая энергия системы материальных точек равна половине квадрата модуля вектора скорости v изображающей точки. [ 1 ] Приращение кинетической энергии системы материальных точек за некоторый промежуток времени равно сумме работ внешних и внутренних сил, действующих на материальные точки системы в течение рассматриваемого промежутка времени. [ 2 ] Сумма кинетической энергии системы материальных точек в ее движении по отношению к равномерно вращающейся системе координат, потенциальной энергии и потенциальной энергии центробежных сил инерции сохраняет постоянное значение. [ 3 ] Вопрос № 7 Определение: силы, действующие только по прямой, соединяющей частицы, и зависящие только от расстояния между ними, называются центральными. Следовательно, общим для центральных сил будет следующий силовой закон: Работа любой центральной силы будет: Поэтому любая центральная сила является консервативной, и частица в поле центральных сил обладает потенциальной энергией. Примерами центральных сил могут служить гравитационная, кулоновская и упругая силы. Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой[2]. Распределенные системы, в которых действуют центральные силы, в общем случае[3] не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией)) таких элементарных сил. Вопрос№8 Момент силы — векторнаяфизическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1]. Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях). Вопрос №9 Углова́я ско́рость — векторная величина, являющаяся псевдовектором (аксиальным вектором) и характеризующая скорость вращенияматериальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени: Угловое ускорение- величина, характеризующая быстроту изменения угловойскорости твёрдого тела. Вопрос №10 Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции
где
Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси Если тело вращается вокруг неподвижной оси с угловой скоростью
где Iz - момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия твердого тела вращающегося вокруг неподвижной оси, пропорциональна квадрату угловой скорости. Вопрос № 11 Теорема Кориолиса: При сложном движении абсолютное ускорение точки равно геометрической сумме относительного,переносного и добавочного ускорений. Инвариантность: Если подвижная система отсчета движется параллельно неподвижной системе отсчета с постоянной скоростью, то динамическое уравнение прямолинейного ускоренного движения тела в этой системе отсчёта инвариантно динамическому уравнению ускоренного движения этого же тела относительно неподвижной системы отсчета. Это доказывает физическую и математическую инвариантность второго закона Ньютона преобразованиям Галилея. Главным является то, что описанные явления и их закономерности не зависят от скорости движения подвижной системы координат. Вопрос №12 Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):
где k — коэффициент жёсткости системы. Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды. Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Превращение энергии. Внешняя сила, действующая на колебательную систему, совершает работу, следовательно, в систему поступает энергия энергия, переданная посредством работы внешней силы, расходуется на увеличение механической энергии системы и работу против сил сопротивления (равную в свою очередь, потерям механической энергии). Вопрос № 13 Примеры гармонических осцилляторов Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую изматериальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массы маятника. Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где
Крути́льный ма́ятник (также торсио́нный ма́ятник, враща́тельный ма́ятник) — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью. Если при повороте тела в нити возникает момент силы, пропорциональный углу поворота, то тело будет вращаться по гармоническому закону с периодом
где I — момент инерции тела относительно оси кручения, а K — вращательный коэффициент жёсткости маятника. Крутильный маятник представляет собой очень чувствительный механический прибор. Именно с помощью крутильного маятника изучается, например, гравитационное взаимодействие массивных тел в лаборатории и проверяется закон всемирного тяготенияна субмиллиметровом масштабе. Крутильным маятником является баланс — деталь балансирного механизма механических часов, вращательные колебания которой определяют точность их хода. Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Определения · · · · · · Момент инерции относительно оси, проходящей через точку подвеса:
Вопрос №14 Основные законы гидростатики: Закон Паскаля:Давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях. Закон Паскаля описывается формулой давления:
где
Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться. Измеряется давление в ньютонах на метр квадратный или в паскалях (Па), в честь учёного, открывшего закон, Паскаля. На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические прессы и др. Закон Архимеда: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме тела. Сила называется силой Архимеда:
где Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна. Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха. Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести. Для идеального газа, имеющего постоянную температуру
где
где Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см.Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Постоя́нная Бо́льцмана (
Числа в круглых скобках указывают стандартную погрешность в последних цифрах значения величины. В естественной системе единиц Планка естественная единица температуры задаётся так, что постоянная Больцмана равна единице. Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает. Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов. Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:
где n0 и n - число молекул в единичном объёме на высоте h = 0 и h. Так как
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:
– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n0 – число молекул в единице объёма там, где U = 0. Вопрос № 15 Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесиифаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными. Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1]. Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности Проявления Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности: · в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма). · струя воды «сливается» в цилиндр. · маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так каксила тяготения оказывается уравновешенной силой поверхностного натяжения. · некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения. · На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли. Лапласово давление - это давление под искревлённой поверхностью жидкости. представьте поверхность воды, из которой виднеется стеклянная трубка- она капилляр. величина и знак лапласового давления находятся по формулам, потому что при поднятии и при отпускании жидкости через капилляр, давление жидкости должно быть одиниково для всех уровней данного капилляра. Пусть: r- внутренний радиус поперечногог сечения кипилляра r- плотность жидкости g- ускорение свободного падения Po- нормальное атмосферное давление h- высота капилляра Pл- лапласово давлениеъ на поверхности жидкости давление Р=Ро. внутри капилляра: Р=Ро+rgh+Рл. приравняем части равенства и получим: Рл=-rgh. учтите- что под вогнутым мениском давление отрицательно, а под выпуклым- положительно. чем меньше радиус кривизны мениска, тем больше порд ним давление. капиллярность — явление, подъема или опускания жидкости в капиллярах, заключающееся в способностижидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах. В поле тяжести (или сил инерции, например при центрифугировании пористых образцов) поднятие жидкости происходит в случаях смачивания каналов жидкостями, например воды в стеклянных трубках, песке, грунте и т. п. Понижение жидкости происходит в трубках и каналах, не смачиваемых жидкостью, например ртуть в стеклянной трубке. Благодаря капиллярности возможны жизнедеятельность животных и растений, различные химические процессы, бытовые явления (например, подъём керосина по фитилю в керосиновой лампе, вытирание рук полотенцем) Когезия — связь между молекулами (атомами, ионами) внутри тела в пределах одной фазы. Когезия характеризует прочность тела и его способность противостоять внешнему воздействию. Описание: Основой когезии могут являться силы межмолекулярного взаимодействия, включая водородную связь, и/или силы химической связи. Они определяют совокупность физических и физико-химических свойств вещества: агрегатное состояние, летучесть,растворимость, механические свойства и т. д. Интенсивность межмолекулярного и межатомного взаимодействия, а, следовательно, и сил когезии резко убывает с расстоянием. Наиболее сильна когезия в твёрдых телах и жидкостях, то есть в конденсированных средах, где расстояния между молекулами (атомами, ионами) малы, порядка нескольких ангстрем. В газахсредние расстояния между молекулами велики по сравнению с их размерами, поэтому когезия в них незначительна. Мерой интенсивности межмолекулярного взаимодействия служит плотность энергии когезии. Она эквивалентна работе удаления взаимно притягивающихся молекул на бесконечно большое расстояние друг от друга, что в первом приближении соответствует испарению или сублимации вещества. Адгезия (от лат. adhaesio — прилипание) в физике — сцепление поверхностей разнородных твёрдых и/или жидких тел. Адгезия обусловлена межмолекулярными взаимодействиями (Ван-дер-Ваальсовыми, полярными, иногда —химическими или взаимной диффузией) в поверхностном слое и характеризуется удельной работой, необходимой для разделения поверхностей. В некоторых случаях адгезия может оказаться сильнее, чем когезия, то есть сцепление внутри однородного материала, в таких случаях при приложении разрывающего усилия происходит когезионный разрыв, то есть разрыв в объёме менее прочного из соприкасающихся материалов. Наиболее известные адгезионные эффекты — капиллярность, смачиваемость/несмачиваемость, поверхностное натяжение, мениск жидкости в узком капилляре, трение покоя двух абсолютно гладких поверхностей. Критерием адгезии в некоторых случаях может быть время отрыва слоя материала определенного размера от другого материала в ламинарном потоке жидкости. Вопрос №16 Вопрос №17 Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.015 с.) |

 , проведенным из начала отсчета в данную точку А. Этот вектор называется радиус – вектором точки А. Траектория движения будет определяться функцией
, проведенным из начала отсчета в данную точку А. Этот вектор называется радиус – вектором точки А. Траектория движения будет определяться функцией  тела при его движении за единицу времени.
тела при его движении за единицу времени. , а зависимость угла поворота точки от времени является линейной:
, а зависимость угла поворота точки от времени является линейной: ,
, — начальное значение угла поворота.
— начальное значение угла поворота. .
. , а вторая — на первую с силой
, а вторая — на первую с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия 

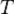 — полная кинетическая энергия системы,
— полная кинетическая энергия системы,  — кинетическая энергия движения центра масс,
— кинетическая энергия движения центра масс,  — относительная кинетическая энергия системы[2].
— относительная кинетическая энергия системы[2].
 , следовательно, результат интегрирования не зависит от пути и определяется
, следовательно, результат интегрирования не зависит от пути и определяется .
. тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела
тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между осями[1]:
между осями[1]:
 — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела, — масса тела,
— масса тела,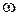 , то линейная скорость i -ой точки равна u I = w ri , где ri - расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует:
, то линейная скорость i -ой точки равна u I = w ri , где ri - расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует: , (5.18)
, (5.18)


 ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция
― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция  ― это угол отклонения маятника в момент
― это угол отклонения маятника в момент  от нижнего положения равновесия, выраженный в радианах;
от нижнего положения равновесия, выраженный в радианах; 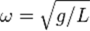 , где
, где  ― длина подвеса,
― длина подвеса,  ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: .
.
 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — начальный угол отклонения маятника;
— начальный угол отклонения маятника;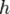 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.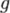 — ускорение свободного падения.
— ускорение свободного падения. .
. ,
, — это давление,
— это давление,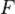 — приложенная сила,
— приложенная сила, — площадь сосуда.
— площадь сосуда.
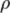 — плотность жидкости (газа),
— плотность жидкости (газа),  — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
— объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма. и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения
и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения  одинаково), барометрическая формула имеет следующий вид:
одинаково), барометрическая формула имеет следующий вид:
 — давление газа в слое, расположенном на высоте
— давление газа в слое, расположенном на высоте  ,
,  — давление на нулевом уровне (
— давление на нулевом уровне ( ),
),  — молярная масса газа,
— молярная масса газа,  — универсальная газовая постоянная,
— универсальная газовая постоянная,  (или плотность газа) убывает с высотой по тому же закону:
(или плотность газа) убывает с высотой по тому же закону:
 — масса молекулы газа,
— масса молекулы газа,  — постоянная Больцмана.
— постоянная Больцмана.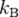 ) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в Международной системе единиц (СИ) равно:
) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в Международной системе единиц (СИ) равно: Дж/К[1].
Дж/К[1].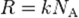 . Газовая постоянная более удобна, когда число частиц задано в молях.
. Газовая постоянная более удобна, когда число частиц задано в молях.
 а
а  , то (2.5.1) можно представить в виде
, то (2.5.1) можно представить в виде
 ,
,
 — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
— сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр. Но более правильно дать определение поверхностному натяжению, как энергии (Дж) на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.


