
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение твердого тела вокруг неподвижной оси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим вращение абсолютно твердого тела вокруг неподвижной оси. Под абсолютно твердым телом понимают такое, у которого остаются неизменными расстояния между любыми его точками. Такое тело не может испытывать деформаций.При вращении такого тела вокруг неподвижной оси каждая его точка описывает дугу окружности с центром, лежащим на оси, причем все такие окружности лежат в параллельных плоскостях и все дуги содержат одинаковое число дуговых градусов. Так как положение неподвижной оси задано, а расстояние между двумя любыми точками остается неизменным, определить положение тела в пространстве можно с помощью всего одного числа. Этим единственыи числом может быть, например, угол φ, на который повернуто тело вокруг оси относительно некоторого своего положения, принятого за нулевое. При вращении тела вокруг неподвижной оси угол φ меняется с течением времени. Вопрос №10 Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции
где
Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси Если тело вращается вокруг неподвижной оси с угловой скоростью
где Iz - момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия твердого тела вращающегося вокруг неподвижной оси, пропорциональна квадрату угловой скорости. Вопрос № 11 Теорема Кориолиса: При сложном движении абсолютное ускорение точки равно геометрической сумме относительного,переносного и добавочного ускорений. Инвариантность: Если подвижная система отсчета движется параллельно неподвижной системе отсчета с постоянной скоростью, то динамическое уравнение прямолинейного ускоренного движения тела в этой системе отсчёта инвариантно динамическому уравнению ускоренного движения этого же тела относительно неподвижной системы отсчета. Это доказывает физическую и математическую инвариантность второго закона Ньютона преобразованиям Галилея. Главным является то, что описанные явления и их закономерности не зависят от скорости движения подвижной системы координат. Вопрос №12 Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):
где k — коэффициент жёсткости системы. Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды. Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Превращение энергии. Внешняя сила, действующая на колебательную систему, совершает работу, следовательно, в систему поступает энергия энергия, переданная посредством работы внешней силы, расходуется на увеличение механической энергии системы и работу против сил сопротивления (равную в свою очередь, потерям механической энергии). Вопрос № 13 Примеры гармонических осцилляторов Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую изматериальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массы маятника. Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где
Крути́льный ма́ятник (также торсио́нный ма́ятник, враща́тельный ма́ятник) — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью. Если при повороте тела в нити возникает момент силы, пропорциональный углу поворота, то тело будет вращаться по гармоническому закону с периодом
где I — момент инерции тела относительно оси кручения, а K — вращательный коэффициент жёсткости маятника. Крутильный маятник представляет собой очень чувствительный механический прибор. Именно с помощью крутильного маятника изучается, например, гравитационное взаимодействие массивных тел в лаборатории и проверяется закон всемирного тяготенияна субмиллиметровом масштабе. Крутильным маятником является баланс — деталь балансирного механизма механических часов, вращательные колебания которой определяют точность их хода. Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.241.235 (0.007 с.) |


 тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела
тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между осями[1]:
между осями[1]:
 — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела, — масса тела,
— масса тела, , то линейная скорость i -ой точки равна u I = w ri , где ri - расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует:
, то линейная скорость i -ой точки равна u I = w ri , где ri - расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует: , (5.18)
, (5.18)


 ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция
― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция  ― это угол отклонения маятника в момент
― это угол отклонения маятника в момент  от нижнего положения равновесия, выраженный в радианах;
от нижнего положения равновесия, выраженный в радианах; 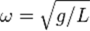 , где
, где  ― длина подвеса,
― длина подвеса,  ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: .
.



