
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение плоскости общего положения до положения проецирующей.Содержание книги
Поиск на нашем сайте
При вращении плоскости вокруг оси, перпендикулярной к плоскости проекций Для то, чтобы плоскость общего положения перевести в положение фронтально-проецирующей, ось вращения следует брать перпендикулярной Для необходимого в этих случаях угла поворота удобно пользоваться главными линиями плоскости (рис.11). Определение истинной величины геометрических элементов, лежащих в плоскости общего положения осуществляется последовательным поворотом этой плоскости вокруг двух осей перпендикулярных плоскостям проекций (рис.12).
6.2. Вращение плоскости вокруг осей, параллельных плоскостям проекций.
Вращение плоскости общего положения до положения, параллельного одной из плоскостей проекций, может быть произведено вокруг одной из ее главных линий (рис.13).
При этом необходимо отметить, что при вращении точки вокруг оси параллельной плоскости проекций эта точка движется в плоскости Определение истинной величины треугольника АВС вращением вокруг горизонтали показано на рис.14. Ось вращений h проходит через точку С, которая остается неподвижной, то есть С1 Точка А находится на стороне треугольника В1А, кроме того она вращается вокруг h в плоскости
ЛЕКЦИЯ 7 7.1. ГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
Гранные поверхности образуются перемещением прямолинейной образующей ℓ по ломаной направляющей m. При этом, если одна точка S образующей неподвижна, получается парамидальная поверхность, если же при перемещении образующая параллельна заданному направлению, то создается призматическая поверхность (рис.1).
Элементами гранных поверхностей являются: вершина S (у призматических поверхностей она находится в бесконечности), грань (часть плоскости, ограниченная одним участком направляющей m и крайними относительно его положениями образующей ℓ), ребро (линия пересечения смежных граней). Определитель пирамидальной поверхности включает в себя вершину S, через которую проходят образующие, и направляющую: S Определитель призматической поверхности содержит направление n, которому параллельны все образующие ℓ поверхности: ℓ║n, ℓ∩m. Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и равные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например, тетраэдр – правильный четырехгранник, а гексаэдр – куб, октаэдр – многогранник. Пирамида – многогранник, в основании которого лежит произвольный многоугольник, а боковые грани – треугольники с общей вершиной S. На комплексном чертеже пирамида задается проекциями ее вершин и ребер. Видимость ребер определяется с помощью конкурирующих точек (рис.2).
Призма – многогранник, у которого основания – два одинаковых и взаимно параллельных многоугольника, а боковые грани – параллелограммы. Если ребра призмы перпендикулярны плоскости основания, то такую призму называют прямой (рис.3).
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.217 (0.005 с.) |

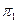 , угол между вращаемой плоскостью
, угол между вращаемой плоскостью 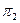 , угол между вращаемой плоскостью и плоскостью
, угол между вращаемой плоскостью и плоскостью 


 перпендикулярной как к оси вращения, так и к той плоскости проекций, какой ось вращения параллельна. Отсюда следует, что одна проекция вращающейся точки всегда будет находиться на линии пересечения проецирующей ее плоскости с плоскостью проекций. Вторая проекция точки движется по эллипсоиду.
перпендикулярной как к оси вращения, так и к той плоскости проекций, какой ось вращения параллельна. Отсюда следует, что одна проекция вращающейся точки всегда будет находиться на линии пересечения проецирующей ее плоскости с плоскостью проекций. Вторая проекция точки движется по эллипсоиду. С. Точка В вращается вокруг h по дуге радиуса [ОВ]. Горизонтальная проекция радиуса [О1В1]
С. Точка В вращается вокруг h по дуге радиуса [ОВ]. Горизонтальная проекция радиуса [О1В1] 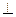 h1, фронтальная проекция - [О2В2]- в проекционном соответствии. По двум проекциям способом треугольника, определяем истинную величину радиуса вращения. Так как точка В вращается вокруг горизонтали в плоскости
h1, фронтальная проекция - [О2В2]- в проекционном соответствии. По двум проекциям способом треугольника, определяем истинную величину радиуса вращения. Так как точка В вращается вокруг горизонтали в плоскости 
 . В пересечении В111А1 и
. В пересечении В111А1 и 


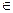 ℓ; ℓ∩m.
ℓ; ℓ∩m.






