
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая параллельная плоскости.Содержание книги Поиск на нашем сайте
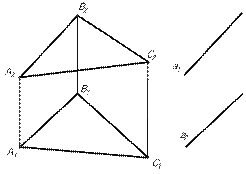
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости (рис.9). а ║[АВ], а1 ║[А1В1], а2 ║[А2В2], задача не имеет единственного решения.
Пересечение прямой с плоскостью.
Для определения точки пересечения прямой а с плоскостью общего положения 1. Через данную прямую а провести вспомогательную проецирующую плоскость а 2. Построить линию пересечения n данной плоскости 3. Определить точку пересечения К прямой а и заданной плоскости К= а ∩n; К1= а1 ∩n1; К2 4. Определяем видимость прямой. Для этого рассматриваем конкурирующие точки 1-3 и 4-5. Точка 1
Рассмотрим конкурирующие точки 4-5; 4
Прямая, перпендикулярная плоскости.
Построение перпендикуляра к плоскости основано на положении геометрии: прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим в этой плоскости и проходящих через точку пересечения перпендикуляра с этой плоскостью (рис.11). Пусть некоторый отрезок прямой [АС] Построим на плоскости Если прямая перпендикулярна к плоскости, то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости. Расстояние от точки до плоскости измеряется отрезком перпендикуляра от точки до его основания на плоскости:
1. Из точки опустить перпендикуляр на плоскость 2. Найти точку встречи перпендикуляра с плоскостью
Пример 1. Определить расстояние от точки М до плоскости 1. В плоскости 2. Находим точку пересечения перпендикуляра n с плоскостью 3. Определяем истинную величину расстояния от точки М до плоскости
Пример 2. Построить плоскость перпендикулярную данной прямой (рис.13). Так как прямая а
Пример 3. Определить расстояние от точки М до прямой b (рис.14).
1. В точке М задаем плоскость 2. Находим точку пересечения прямой b с заданной плоскостью b Истинную величину расстояния определяем способом треугольника.
ПЛОСКОСТИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ Для построения плоскости перпендикулярной к данной, необходимо построить перпендикуляр к ней, затем уже строить плоскость, проходящую через данный перпендикуляр. Так как через прямую можно провести бесчисленное множество плоскостей, то задание имеет множество решений. Пример. В точке D построить плоскость Плоскость
ЛЕКЦИЯ 5 МЕТОДЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА. Многие пространственные задачи в общем виде решаются довольно сложно, однако будучи поставлены в частное положение, решаются легко. Примером может служить одна из основных задач курса: определение расстояния от точки до прямой. Сущность методов преобразования чертежа состоит в том, что задача общего положения переводится в частное, где она решается значительно легче. Будем рассматривать следующие методы преобразования чертежа: 1. Метод перемены плоскостей проекций 2. Метод вращения
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.90 (0.009 с.) |

 (АВС) необходимо выполнить следующие построения (рис.10):
(АВС) необходимо выполнить следующие построения (рис.10): , так как
, так как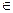


 плоскости
плоскости  и точка А – точка пересечения отрезка прямой с этой плоскостью.
и точка А – точка пересечения отрезка прямой с этой плоскостью.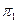 – h1, так как [CA]
– h1, так как [CA]  ; n2
; n2 


 ; b2
; b2 



