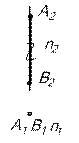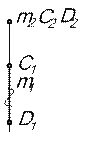Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональная система трех плоскостей проекцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Две проекции точки вполне определяют ее положение в пространстве. Так как каждая фигура или тело представляют собой совокупность точек, то можно утверждать, что две ортогональные проекции предмета вполне определяют его форму. Однако на практике часто возникает необходимость создания дополнительных проекций.
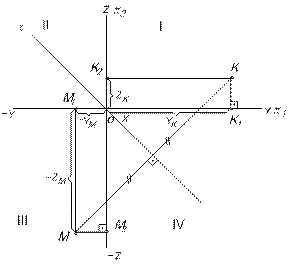
Проекции точек на профильную плоскость проекций называются профильными проекциями – А3. Плоскости проекций попарно пересекаясь определяют три оси ОX; ОY и ОZ, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке О. А1Ау = Х – абсцисса (расстояние от точки до А1Ах= Y - ординат (расстояние от точки до А2Ах = Z - аппликата (расстояние от точки до Длины проецирующих перпендикуляров, определяющих расстояние точки до плоскостей проекций, являются координатами точки. Задание точки осуществляется в следующем виде: А (Х, Y, Z). Знаки координат Х, Y, Z в четырех угловых пространствах показаны в таблице1. Таблица 1
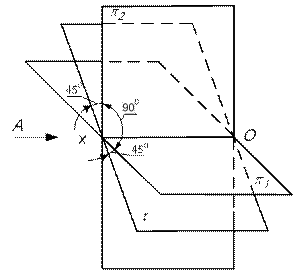
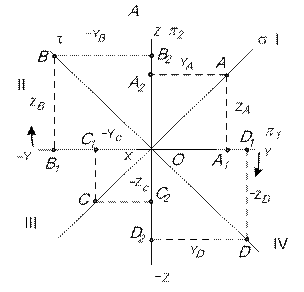
1.5. БИССЕКТОРНЫЕ ПЛОСКОСТИ (ПЛОСКОСТЬ СИММЕТРИИ И ПЛОСКОСТЬ ТОЖДЕСТВА) Плоскость, которая проходит через I и III угловые пространства и делит их пополам, называется плоскостью симметрии и обозначается Плоскость, которая проходит через II и IV угловые пространства и делит их пополам, называется плоскостью тождества и обозначается
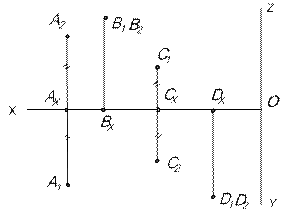
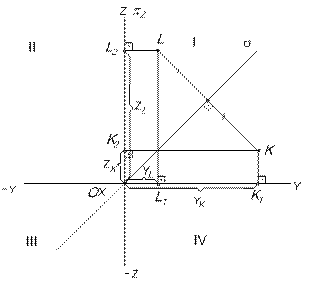
На рис.13 изображен вид А пересекающихся плоскостей Координаты Y и Z точек, лежащих на плоскости симметрии одинаковы по величине и по знаку: Уа = ZА; -УС = ZС. Координаты Y и Z точек, лежащих на плоскости тождества одинаковы по величине, но противоположны по знаку: -УВ = ZВ; УD = - ZD 1.6. ТОЧКИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО БИССЕКТОРНЫХ ПЛОСКОСТЕЙ. Пусть точка L симметрична точке К относительно s (рис.14). Тогда координата YК равна по величине и по знаку координате ZL (YК = ZL), а координата ZК равна по величине и по знаку координате YL (ZК = YL). Координаты Y и Z точек, симметричных относительно плоскости симметрии, равны по величине и по знаку координатам Z и Y заданных точек. Пусть точка М симметрична точке К относительно плоскости тождества
ТОЧКИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Пусть точка В симметрична точке А относительно плоскости
У точек симметричных относительно горизонтальной плоскости проекций Пусть точка С симметрична точке А относительно плоскости проекций Пусть точка D симметрична точке А относительно оси проекций ОХ. У точек, симметричных относительно оси проекций ОХ, координаты Y и Z меняют знак на противоположный YD= -YA; ZD= -ZA. А(Х,Y,Z); D(Х,-Y,-Z).
ЛЕКЦИЯ 2 ПРЯМАЯ ЛИНИЯ Для построения изображения прямой линии на плоскостях проекций достаточно построить проекции двух точек этой прямой (рис.1).
a([ВВ2] || [АА2]) ∩
а –прямая в пространстве, a 1 – горизонтальная проекция прямой, а 2 – фронтальная проекция прямой. Проекция прямой линии есть также прямая линия. Точка, лежащая на прямой линии, имеет свои проекции на соответствующих проекциях прямой. C1 В каком отношении точка делит отрезок прямой линии в пространстве, в таком же отношении проекции этой точки делят соответствующие проекции отрезка.
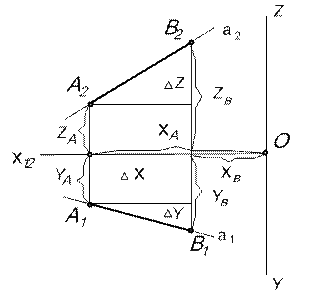
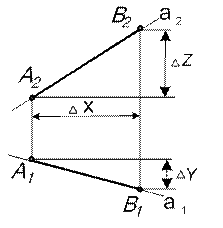
Совмещая плоскости проекций По эпюру с осями можно определить положение точек А и В в пространстве по координатам X, Y, Z. Безосный эпюр точек А и В не определяет их положение в пространстве, но позволяет судить об их относительности ориентировке (рис.2). ∆Х характеризует смещение точки А по отношению к точке В в направлении параллельном
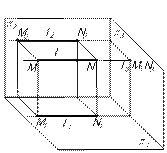
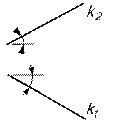
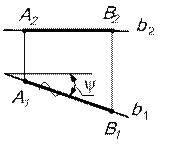
Положение прямой относительно плоскостей проекций. 1. Прямыми общего положения называются прямые, не параллельные ни одной из плоскостей проекций (рис.1, 2, 3).
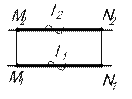
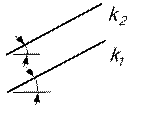
2. Прямые уровня - прямые, параллельные плоскостям проекций. а) Прямые, параллельные горизонтальной плоскости проекций, называются горизонтальными прямыми или горизонталями (рис.4)
[АВ] [А1В1] [А2В2]
b2 ┴ линии связи; b2 ║ ОХ b1 – конгруэнтна самой прямой
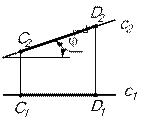
б) Прямая, параллельная
[CD] [C1D1] [C2D2]
c1┴ линии связи c1║ ОХ c2 конгруэнтна самой прямой
в) Прямая, параллельная
[MN] [M1N1] [M2N2]
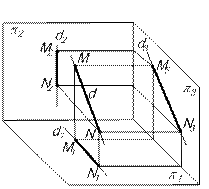
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая, перпендикулярная
Прямая, перпендикулярная
Прямая, перпендикулярная
Прямая, параллельная плоскости симметрии Прямая, параллельная плоскости тождества
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.009 с.) |

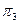 - профильная плоскость проекции [AA3 ]
- профильная плоскость проекции [AA3 ] 
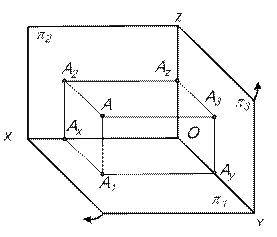

 (рис. 11).
(рис. 11).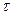 (рис.12).
(рис.12).

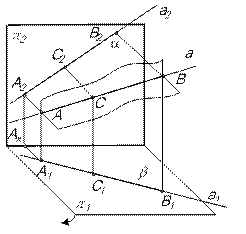
 ([АА1] || [ВВ1]) ∩
([АА1] || [ВВ1]) ∩  [А1В1]; C2
[А1В1]; C2 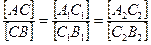 .
.


 В1
В1