Метод замены (перемены) плоскостей проекций

 

Этот метод широко применяют во всех отраслях машиностроения и приборостроения. Сущность этого метода заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система П₁/П₂ заменяется (дополняется) плоскостями, образующими с П₁ или П₂ (или между собой) системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение наиболее удобное для выполнения требуемого построения.

В ряде случаев для получения системы плоскостей проекций, разрешающей поставленную задачу, бывает достаточно ввести (заменить) только одну плоскость, например П₄^П₁ или П₅^П₂ при этом плоскость П₄ окажется горизонтально-проецирующей, а плоскость П₅ – фронтально-проецирующей. Если введение одной плоскости П₄ или П₅ не позволяет решить задачу, то прибегают к последовательному дополнению основной системы плоскостей проекций новыми (П₆, П₇ и т.д.).

На рис. 4.1. показано преобразование проекций точки А из системы П₂/П₁ в систему П₄/П₁, в которой вместо плоскости П₂ введена новая плоскость П₄, а плоскость П₁ осталась неизменной. При этом плоскость П₄ перпендикулярна плоскости П₁. В системе П₄/П₁ горизонтальная проекция А₁ точки А осталась неизменной.

Рис. 4.1

 

Проекция А₄ точки А на плоскость П₄ находиться на плоскости П₁ на том же расстоянии (!!!), что и проекция А₂ точки А на плоскость П₂. это условие позволяет легко строить проекцию точки на новой плоскости проекций (рис. 4.2).

 

Рис. 4.2

 

Для этого в новой системе (П₁/П₄) из проекции точки (А₁) на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную новой оси проекций (П₄/П₁). На этой линии связи отмечают расстояние от оси П₄/П₁ до проекции А₄ точки А на новой плоскости проекций П₄, равное расстоянию от преобразуемой проекции А₂ точки до оси П₂/П₁ |А₄*2| = |А₂ *1|.

При введении новой плоскости проекций, перпендикулярной фронтальной плоскости проекций (например, плоскости П₄ на рис. 4.3), расстояние от проекции (В₄) точки В до новой оси проекций (П₄/П₂) равно расстоянию от горизонтальной проекции (В₁) до оси П₂/П₁ |В₁*1| = |В₄*2|.

 

Рис. 4.3

 

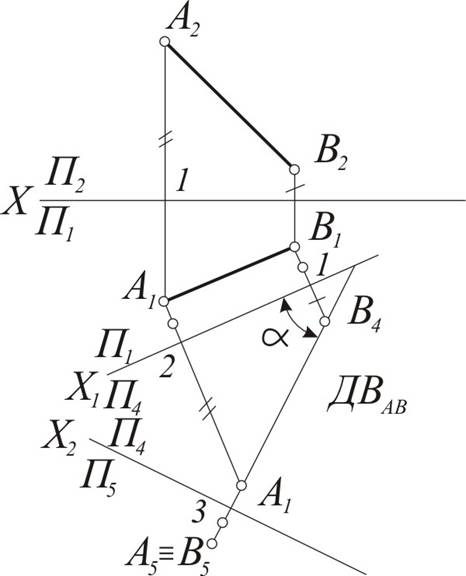
В дальнейшем при введении новой плоскости проекций ось проекций можно обозначать в виде дроби, черта которой лежит на оси; каждую букву при этом пишут как бы на «своей» плоскости.

Определение длины отрезка АВ общего положения (рис. 4.4)

Заменим плоскость П₂ на П₄½½АВ (ось П₁/П₄ ½½А₁В₁). Расстояния от оси П₁/П₄ до А₄ и В₄ равны расстояниям от А₂ и В₂ до оси П₂/П₁ соответственно |А₄*2| = |А₂*1|. Одновременно с определением действительной величины отрезка АВ определена величина a угла наклона к плоскости П₁.

 

Рис. 4.4

 

Приведение отрезка прямой АВ общего положения в проецирующее положение (в продолжение предыдущего примера).

На том же рис. 4.4 новая система плоскостей проекций П₄/П₁ относительно отрезка АВ находиться в частном положении (П₄½½АВ). Введем еще одну плоскость проекций П₅^П₄ и отрезку АВ (ось проекций П₄/П₅^А₄В₄). Относительно этой плоскости проекций П₅ отрезок АВ занимает проецирующее положение (А₅ = В₅, |А₁*2| = |А₅*3|).

Необходимо заметить, сто для преобразования эпюра отрезка общего положения в проецирующее требуется введение двух новых плоскостей проекции последовательно, первой – параллельно отрезку, второй – перпендикулярно ему. При этом должны выполняться условия перпендикулярности исходных и новых плоскостей проекций, а также сохранения координат проекций точек на заменяемых плоскостях проекций.

Приведение плоской фигуры общего положения в проецирующее положение, а также определение её натуральной величины.

На первом этапе задачу решают с помощью одной из линий уровня, например, горизонтали с проекциями А₂F₂, A₁F₁ (рис. 4.5). Новая плоскость проекций П₄ в этом случае выбрана перпендикулярно горизонтали AF (ось П₁/П₄^A₁F₁) и соответственно перпендикулярно плоскости П₁.

 

Рис. 4.5

 

Откладывая на линиях связи от оси П₁/П₄ координаты вершин А, В, и С с плоскости П₂ на плоскость П₄, получим проекции указанных вершин (А₄, В₄ и С₄), которые будут расположены на одной линии (т.е. плоскость DАВС^П₄).

На втором этапе решения задачи (определить натуральную величину треугольника АВС) вводим новую плоскость проекций П₅^П₄ и параллельно плоскости треугольника АВС (т.е. его проекции А₄В₄С₄). Проведя линии связи от А₄, В₄ и С₄ перпендикулярно оси П₄/П₅ и отложив на них от этой оси координаты вершин А, В и С с горизонтальной проекции треугольника АВС на плоскости П₅ (А₅, В₅ и С₅), получим натуральную величину треугольника АВС и углов при его вершинах.

Определение расстояния между двумя скрещивающимися прямыми.

Это расстояние выражается длиной общего перпендикуляра MN к заданным прямым АВ и СD. (рис. 4.6)

Рис. 4.6

 

Для решения этой задачи необходимо, чтобы одна из этих прямых располагалась перпендикулярно плоскости проекций. Для этого необходимо последовательно ввести две новые плоскости проекций (П₄ и П₅) для превращения одной из прямых (например АВ) сначала в линию уровня (с помощью плоскости П₄), а затем в проецирующую (с помощью плоскости П₅), после чего опустить перпендикуляр из проекции слившихся в одну точек А и В (А₅ = В₅) на проекцию С₅D₅ (M₅N₅ – действительно искомое расстояние).