Построение очертаний поверхности на комплексном чертеже.

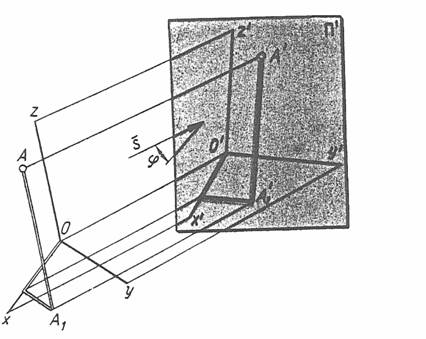
Касательные плоскости широко применяются при решение различных позиционных задач на поверхности.

1. Построение касательных плоскостей к поверхностям является основой теорией теней. При построении теней касательные плоскости к поверхностям строят или проходящими через точку, лежащую на поверхности, или параллельными заданному направлению.

2. Касательными плоскостями к поверхностям конуса и цилиндра, параллельными заданному направлению, пользуются для определения наиболее близкой и наиболее удаленной от плоскостей проекций точек кривой линии пересечения этих тел плоскостью общего положения, не строя эти кривые (см. Бубеннщив § 68).

3. Касательные плоскости используют при построении соприкасающихся однополосных гиперболоидов вращения при проектировании гиперболических зубчатых колес. В передачах с перекрещивающимися валами. (см. Бубеннщив § 68)

4. Касательные плоскости применяются и при построении очертаний поверхностей (очерков).

Рассмотрим эту задачу более подробно.

Как известно, очерк поверхности (тела) получается как проекция контурной линии на заднюю плоскость проекций (например П₁) (см. рис. 7.5). Напомним, что контурная линия – это линия, по которой множество плоскостей Р, перпендикулярных плоскости П₁, касаются данного тела Т (рис. 10.13). Огибающей этого семейства касательных плоскостей будет некоторая цилиндрическая лучевая поверхность Ф, тоже перпендикулярная П₁.

 

Рисунок 10.13

 

Контурная линия m делит тело на две части, одна из которых видимая на заданной плоскости проекций П₁, а другая невидимая. В любой точке на контурной линии обе поверхности – тело и цилиндрическая лучевая – имеют общую касательную плоскость Р. Линия пересечения m₁ лучевой цилиндрической поверхности Ф с плоскостью П₁ и является очерком тела. Если при этом принять, что цилиндрическая лучевая поверхность состоит из световых лучей, касающихся непрозрачного тела, то очерк тела – линия, ограничивающая тень тела на плоскости П₁. Эту линию на плоскостях проекций называют также линией видимости.

На рисунке 10.13 видно, что очерком шара плоскости П₁ будет проекция экватора m (m₁), которая на плоскость П₂ спроецируется в виде прямой параллельной оси ОХ. Очерком шара на плоскости П₂ будет проекция его главного меридиана.

На рисунке 10.14 будет прямоугольник (главный меридиан). Очерк на плоскости П₁ определяется двумя касательными лучевыми плоскостями перпендикулярными к плоскости П₁. Эти плоскости касаются цилиндра по двум крайним образующим АВ и СD, проекции которых на плоскости П₂ совпадают. Горизонтальные проекции А₁В₁ и С₁D₁ вместе с наружными поверхностями (проекциями кругов оснований) и определяют очерк цилиндра на плоскости П₁.

 

Рисунок 10.14

 

В общем случае для построения очерка тела на плоскости П₁ надо сначала на плоскости П₂ построить проекцию контурной линии, по которой тело обертывается цилиндрической лучевой поверхностью, а затем спроецировать ее на плоскость П₁.

Построение контурной линии проще всего осуществить с помощью вписанных сфер.

 

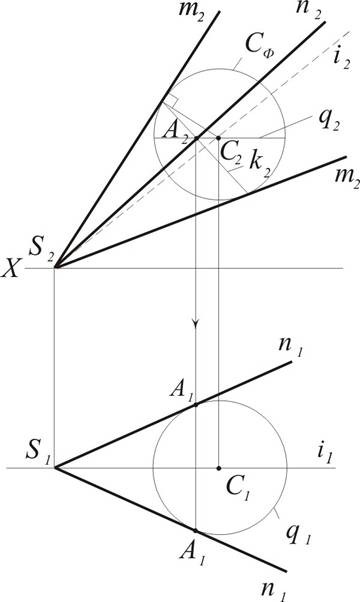
Пример 8. Построить на горизонтальной проекции очерк конуса, ось которого i параллельна плоскости П₂ и наклонена к плоскости П₁. (рис. 10.15)

Решение. Не трудно видеть, что очерк конуса на плоскости П₂, ограниченный главным меридианом m, полностью задает форму поверхности конуса.

 

Рисунок 10.15

 

А для построения горизонтального очерка из любой точки С (С₂) лежащей на оси i, проводим сферу, касающуюся конуса по окружности k (k₂). Ее фронтальная проекция является прямой перпендикулярной оси (i₂), как соосные тела.

Проводим через центр сферы экватор q₂ и находим точку А₂ его пересечение с окружностью k₂. Соединив точки S₂ и А₂ получим контурную линию. Спроецировав точку А₂ на горизонтальную проекцию экватора получим две точки А₁, которые вместе с вершиной S₁ и задают горизонтальный очерк контура n₁. Заметим, что фронтальная проекция n₂ горизонтального очерка не совпадает с проекцией оси i₂.

 

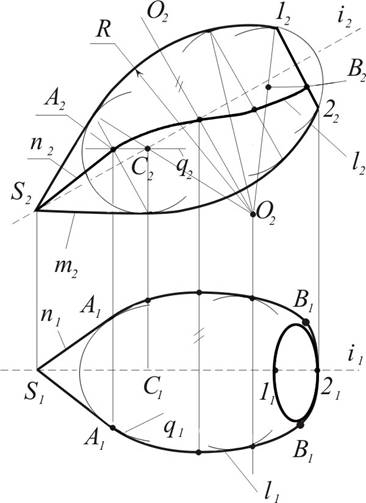
Пример 9. Построить на горизонтальной проекции П₁ Очерк деталей вращения, ось I которой параллельна плоскости П₂ и наклонена к плоскости П₁. Поверхность детали состоит из конуса вращения (S, k) и тора, образующей которого является дуга окружности радиусом R с центром в точке О. (рис. 10.16)

 

Рисунок 10.16

Решение:

1. Очерк фронтальной проекции – это главный меридиан – полностью задает форму детали.

2. Очерк горизонтальной проекции составляется из эллипса верхнего основания, пространственной кривой и очерка конуса.

3. Эллипс строим по двум осям – малой 1₁2₁ и большой 1₂2₂.

4. Очерк конуса строим по примеру 8 (рис. 10.15).

5. Далее необходимо построить контурную l₂ линию, по которой цилиндрическая лучевая поверхность перпендикулярная к плоскости П₁, касается поверхности тора.

6. Для построения контурной линии на поверхности тора впишем в него ряд сфер. Центры сфер С₂ лежат в точках пересечения оси вращения i₂ с радиусом R, проведенным из точки О₂ к меридиану. Сферы касаются тора по параллелям k₂.

7. Плоскости, касательные к тору, являются касательными и вспомогательных сфер в точках А₂ пересечения экваторов q₂ сфер параллелями k₂.

8. Горизонтальные проекции А₁ этих точек определяются в пересечении линий связи с горизонтальной проекцией экватора q1.

9. Аналогичными построениями находят еще ряд точек (например В₂). Множество точек образуют контурную пространственную кривую l₂.

10. Горизонтальная проекция l₁ даст очертания тора.

11. Итак, очерком детали является составная плоская кривая из очерков контура n₁, тора l₁ и эллипса.

 

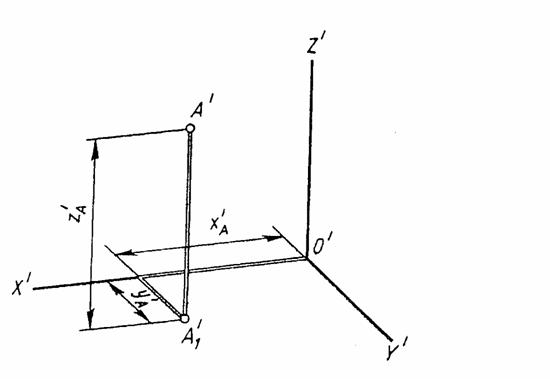
Глава 11

Аксонометрические проекции.

11.1. Основные понятия и определения.

Аксонометрические изображения широко применяются благодаря хорошей наглядности и простоте построения.

Слово «аксонометрия» в переводе с греческого означает измерение по осям. Аксонометрический метод может сочетаться и с параллельным, и с центральным проецированием при условии, что предмет проецируется вместе с координатной системой.

Сущность метода параллельного аксонометрического проецирования заключается в том, что предмет относят к некоторой системе координат и затем проецируют параллельно лучам на плоскость вместе с координатной системой.

На рисунке 11.1 показана точка А, отнесенная к системе прямоугольных координат xyz.

Проекции координатных осей пространственной системы называются аксонометрическими осями.

Рисунок 11.1

 

Вектор определяет направление проецирования на картинную плоскость П´ (плоскость проекций).

Для создания аксонометрической (в нашем случае параллельной) проекции точки А проведем через нее проецирующий луч (параллельно вектору ) и найдем пересечение его с плоскостью П´ в точке А´. это построение показывает, что при заданном направлении проецирования каждой точке А пространства на плоскости проекций соответствует определенная точка А´.

Но обратное, как известно, утверждать нельзя. Действительно, каждой точке А´ на плоскости П´ соответствует любая точка проецирующего луча А´А.

Для того чтобы устранить эту неопределенность и обеспечить взаимную однозначность между точками пространства и точками картинной плоскости, поступают следующим образом: на плоскости П´ проецируют не только точку А, но и одну из ее ортогональных проекций (обычно горизонтальную проекцию А₁).

Аксонометрическую проекцию А´₁, горизонтальной проекции точки А принято называть вторичной проекцией.. Этот термин хорошо выражает тот факт, что точка А´₁ получается в результате двух последовательных проецирований.

Рассмотрение того же рисунка 11.1 позволяет сделать вывод о том, что если заданы система координат xyz, направление проецирования , и плоскости П´, то аксонометрическая проекция и ее вторичная проекция однозначно определяют положение точки в пространстве. Действительно, проведя через вторичную проекцию А´₁ точки А прямую, параллельную , и определив точку пересечения этой прямой с координатной плоскостью xOy, найдем горизонтальную проекцию А₁ точки А. Положение же точки А в пространстве определяется пересечением двух прямых А´А и А₁А, первая из которых проходит через А´ параллельно , а вторая – через А₁ перпендикулярно плоскости xOy.

На плоскости картины П´ (рисунок 11.1) показана и аксонометрическая проекция осей координат – плоская система x´y´z´. В общем случае длина отрезков осей координат в пространстве не равна длине их проекций.

Искажение отрезков осей координат при их проецировании на плоскость П´ характеризуется так называемыми коэффициентами искажения. Коэффициентом искажения называется отношение длины проекции отрезка оси на картине к его истинной длине. Так, коэффициент искажения по оси x´ u = , по оси y´ v = и по оси z´ w = (рисунок 11.1).

Зная коэффициенты искажения и свойства взаимного расположения точек, линий и плоскости фигур, которые сохраняются при их параллельном проецировании, можно построить аксонометрическое изображение точки А. это изображение определяется как граничная точка координатной ломанной, состоящей из отрезков длиной x´_A, y´_A, z´_A, отложенных от начала аксонометрических осей О´ на соответствующих прямых, параллельных этим осям (рисунок 11.2) или совпадающих с ними.

Рисунок 11.2

Построение координатной ломанной требует измерения трех прямоугольных координат точки x, y, z, перевода их при помощи коэффициентов искажения в аксонометрические и, наконец, вычерчивание этой ломаной, при построении которой попутно находится и одна из вторичных проекций точки.

 

11.2. Виды аксонометрических проекций.

В зависимости от соотношения коэффициентов искажения, аксонометрические проекции могут быть:

- изометрическими, если коэффициенты искажения по всем трем осям равны между собой; в этом случае u = v = w;

- диметрическими, если коэффициенты искажения по двум любым осям равны между собой, а по третьей – отличается от первых двух;

например, u = v ≠ w;

- триметрическими, если все три коэффициента искажения по осям различны, т.е. когда u ≠ v ≠ w, u≠w.

Аксонометрические проекции различаются так ж е и по тому углу φ, который образуется проецирующим лучом с плоскостью проекции П´. Если φ≠90⁰, то аксонометрическая проекция называется косоугольной, а если φ = 90⁰ – прямоугольной.

Естественно, что изометрические, диметрические и триметрические проекции могут быть как прямоугольными, так и косоугольными.