Плоскости общего и частного положения

 

Различают частные и общие случаи расположения плоскости в пространстве относительно плоскостей проекций.

 

Плоскость общего положения. Плоскость, произвольно расположенная по отношению к плоскостям проекций, называется плоскостью общего положения (рис. 3.1).

Проекции элементов, которыми задана такая плоскость (точки, прямые, следы плоскости, плоские фигуры), составляют случайные углы с линиями связи и осями проекций комплексного чертежа, т.е. располагаются произвольно и ни в одной проекции на вырождаются в более простой геометрический образ.

Плоскости, перпендикулярные одной или двум плоскостям проекций называются плоскостями частного положения.

Плоскость, перпендикулярная к плоскости проекций называется проецирующей плоскостью. Проецирующая плоскость, перпендикулярная к горизонтальной плоскости проекций называется горизонтально-проецирующей, к фронтальной – фронтально-проецирующей, к профильной – профильно-проецирующей.

В прямоугольных проекциях плоскость, перпендикулярная к плоскости проекций, параллельна направлению проецирования и поэтому является проецирующей. Её проекция на этой плоскости вырождается в прямую; проекция на другую плоскость является неограниченным полем точек.

 

Горизонтально-проецирующая плоскость. Фронтальной проекцией плоскости Р^П₁ является неограниченное поле точек (табл. 3.2, п.1), горизонтальной – прямая Р₁. Горизонтальная проекция любой линии (точки, фигуры), лежащей в горизонтально-проецирующей плоскости, располагается на выродившейся в прямую горизонтальной проекции этой плоскости.

 

Фронтально-проецирующая плоскость. Горизонтальная проекция плоскости Р^П₂ представляет собой неограниченное поле точек (табл. 3.2, п.2), фронтальная проекция Р₂ вырождается в прямую. Фронтальная проекция любой точки, линии или фигуры, лежащих во фронтально-проецирующей плоскости, располагаются на выродившейся в прямую фронтальной проекции этой плоскости.

 

Профильно-проецирующая плоскость. Профильная проекция плоскости Р^П₃, вырождается в прямую (табл. 3.2., п.3). Проекциями на плоскость П₁ и П₂ являются неограниченные поля точек. Профильная проекция любой линии (точки, фигуры), лежащей в профильно-проецирующей плоскости, располагается на выродившейся в прямую профильной проекции этой плоскости. Из рисунков в таблице 3.2. видно, что один след проецирующей плоскости (так называемый след-проекция) совпадает с выродившейся в прямую проекцией плоскости, а другой- перпендикулярен к оси проекций.

Задание на комплексном чертеже проецирующих плоскостей следами изображено в таблице 3.2. и не нуждается в пояснениях (сопоставьте изображения каждой проецирующей плоскости в таблице).

Заметим, что угол между следом-проекцией и осью проекции равен углу наклона проецирующей плоскости к плоскости проекций.

На комплексном чертеже проецирующие плоскости чаще изображаются не следами, а своей проекцией, выродившейся в прямую. Вторая проекция, представляющая поле точек, безгранична и обычно не изображается и не обозначается.

 

Таблица 3.2 Положение плоскости относительно плоскости проекций.

 

№	Положение плоскости в пространстве	Наглядное изображение	Эпюр	Положение следов плоскости
	Перпендикулярна плоскости П1 – горизонтально-проецирующая плоскость		Р1 – произвольно Р2 – перпендикулярно к оси X Р3 – перпендикулярно к оси Y
	Перпендикулярна к плоскости П2 – фронтально-проецирующая плоскость		Р1 – перпендикулярно к оси X Р2 – произвольно Р3 – перпендикулярно к оси Z
	Перпендикулярна к плоскости П3 – профильно-проецирующая плоскость		Р1 и Р2 – параллельны к оси X Р3 - произвольно
	Параллельна плоскости П1 – горизонтальная плоскость		Р1 – отсутствует Р2 – параллельно оси X Р3 – параллельно оси Y
	Параллельна плоскости П2 – фронтальная плоскость		Р1 – параллельно оси X Р2 – отсутствует Р3 – параллельно оси Z
	Параллельна плоскости П3 – профильная плоскость		Р1 и Р2 – перпендикулярно к оси X Р3 - отсутствует

 

 

Плоскость, параллельная плоскости проекций называется плоскостью уровня. Такая плоскость перпендикулярна к двум другим плоскостям проекций и, следовательно, по отношению к ним является проецирующей и проецируется на них в прямую линию. Плоскость, параллельная горизонтальной плоскости проекций называется горизонтальной, параллельная фронтальной – фронтальной и параллельная профильной – профильной плоскостью уровня.

В таблице 3.2. п. 4, 5, 6 изображены плоскости параллельные плоскостям проекций – плоскости уровня. Здесь же даны изображения этих плоскостей на комплексном чертеже.

Плоскости уровня не имеют следа на параллельной себе плоскости проекций и проецируются на неё в неограниченные поля точек (эти проекции на комплексном чертеже не обозначаются и не ограничиваются).

Итак, положение плоскостей уровня подчинено общему правилу: если плоскость параллельна плоскости проекций, то на эту плоскость она проецируется в поле точек. Её проекция на другой плоскости – прямая, перпендикулярная к линии связи.

Главные линии плоскости

 

В плоскости можно расположить бесчисленное количество прямых, среди которых будут линии уровня плоскости, т.е. прямые, параллельные плоскостям проекций, и прямые, перпендикулярные к этим линиям уровня, так называемые линии наибольшего уклона плоскости. Такие прямые называются главными (или особыми) линиями плоскости. К первым относятся горизонтальные линии плоскости (горизонтали плоскости), а также фронтальные и профильные (фронтали плоскости, профильные прямые плоскости).

Главные линии плоскости имеют большое практическое применение. Например при помощи горизонталей изображаются части поверхности земляных сооружений, ограниченные плоскостями (откосы насыпей и выемок, плотин и т.п.), определяются их контуры на планах и т.д. Горизонталями плоскости – напластования горных пород, ориентируется положение пласта породы по отношению к сторонам света (простирание), а линией наибольшего уклона указывается положение этого пласта по отношению к плоскости горизонта (падение).

Горизонтали и фронтали плоскости широко используются при решении различных задач начертательной геометрии. Задание плоскости этими линиями имеет ряд преимуществ перед другими способами задания её.

Горизонтали плоскости. Горизонтальными линиями уровня плоскости называются прямые, лежащие в этой плоскости и параллельные горизонтальной плоскости проекций.

 

Рис. 3.3

 

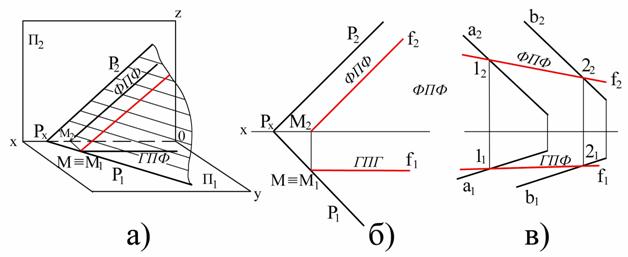
Горизонтальную линию уровня любой плоскости можно рассматривать как линию пересечения этой плоскости с горизонтальной плоскостью уровня. Горизонтальную плоскость проекций П₁ можно принять за горизонтальную плоскость нулевого уровня. Поэтому горизонтальный след Р₁ плоскости можно принять за горизонтальную линию нулевого уровня этой плоскости.

Все горизонтали плоскости, в том числе её горизонтальный след взаимно параллельны как линии пересечения одной плоскости с параллельными плоскостями уровня.

На рис. 3.3, а изображена плоскость Р, заданная следами Р₁ и Р₂, горизонталь h и ее проекции h₁ и h₂. Для построения проекций горизонтали на комплексном чертеже (рис. 3.3, б) проведена проекция h₂||ОХ, построены проекции N₂=h₂ÇP₂ и N₁ÎОХ фронтального следа N горизонтали и через N₁ проведена проекция h₁||P₁. Построенная горизонталь h находится в плоскости Р, так как она проходит через точку NÎP и параллельна прямой Р₁ÎР.

На рис.3.3, в показана горизонталь А1, построенная в плоскости треугольника АВС.

Фронтали плоскости. Фронтальными линиями уровня плоскости называются прямые, лежащие в этой плоскости и параллельные фронтальной плоскости проекций.

Проведя рассуждения, аналогичные рассмотренным для горизонтали, придем к выводу, что фронтали плоскости параллельны фронтальному следу Р₂ плоскости, являющемуся фронтальной линией нулевого уровня этой плоскости.

Плоскость Р, заданная следами Р₁ и Р₂, фронталь f и её проекции f₁ и f₂ изображены на рис 3.4, а.

рис 3.4

 

Для построения проекций фронтали на комплексном чертеже (рис 3.4, б) проведена проекция f₁||ОХ, построены проекции М₁=f₁ÇР₁ и М₁ÎОХ горизонтального следа М фронтали и через М₂ проведена проекция f₂||Р₂. Построенная фронталь fÎР, т.к. она проходит через точку МÎР и параллельна прямой Р₂ÎР.

Линия наибольшего уклона (ската) плоскости.

Из всех линий, расположенных в плоскости, прямая, идущая под прямым углом к горизонталям (рис. 3.5,а), наклонена к плоскости П₁ под наибольшим углом – линия наибольшего ската плоскости (ЛНС). Её горизонтальная проекция составляет прямой угол с горизонтальным следом плоскости и с горизонтальными проекциями горизонталей. Поэтому ЛНС следует начинать строить с горизонтальной проекции (рис. 3.5, б), которая расположена по прямым углом к следу Р₁ и к горизонтальной проекции горизонтали. Отметив на горизонтальной проекции линии наибольшего ската две точки М₁ и А₁, строим их фронтальные проекции. Фронтальная проекция линии наибольшего ската пройдет через точки М₂ и А₂. Построение линии наибольшего ската на плоскости, заданной треугольником АВС, показано на рис. 3.5, в, где сначала перпендикулярно к горизонтальной проекции горизонтали проведена горизонтальная проекция 1₁-2₁, а затем фронтальная проекция 1₂-2₂ этой линии.

Угол a наклона линии наибольшего ската к плоскости П₁ определяет наклон плоскости Р к плоскости П_!.

 

Рис. 3.5