Построение теней геометрических тел

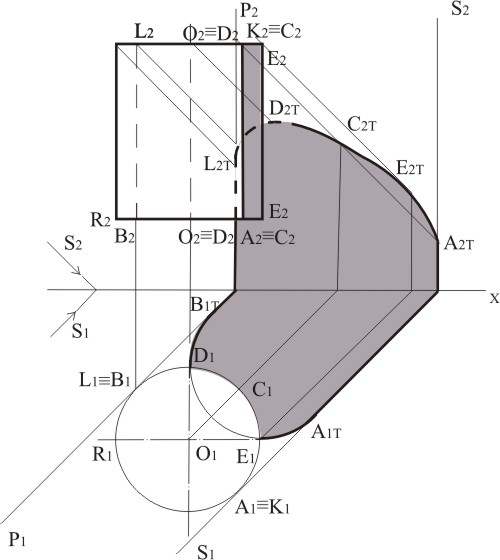
При построении проекций теней геометрических тел необходимо различать собственную и падающие тени. Собственная тень будет на неосвещенной части тела, а падающая тень получается на плоскости или другой поверхности вследствие того, что на пути лучей света расположено геометрическое тело.

Определение собственной и падающей теней сводится к нахождению их контуров, т.е. линий, отделяющих освещенную часть поверхности тела от неосвещенной (рис.12.19).

Контуром собственной тени многогранника является ломаная линия АтКтЕтДтСтВт, контур падающей тени проходит через точки АКЕДВС.

Контуром собственной тени сферы будет окружность, которая получится в сечении сферы плоскостью, перпендикулярной к лучам света и проходящей через центр.

 

Рис. 12.19

При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения теней от вершин и сторон ломаной линии или точек кривой линии, являющейся контуром собственной тени.

В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени, если ее построить от всех точек и линий геометрического тела.

Указанные приемы и положены в основу построения собственных и падающих теней геометрических тел.

Рассмотрим процесс построения проекций собственных и падающих теней от основных геометрических тел.

Тени призмы. Контур тени от призмы определяется тенями ее ребер (рис. 12.20).

 

Рис. 12.20 Рис. 12.21

Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости П1, то их освещенность легко определить по горизонтальной проекции (рис. 12.21), где видно, что обращенными к свету являются две грани АА1Д1Д и ДД1С1С. Кроме того, освещено верхнее основание призмы. Таким образом, контуром собственной тени является ломаная АА1В1С1СДА, от которой построена тень, падающая на плоскости проекций П1 и П2 по правила изложенным в разделе 12.3.

Тень пирамиды. На рис 12.22 показано построение тени от пятиугольной пирамиды. Боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, как у призмы, поэтому определить их освещенность по горизонтальной проекции без дополнительных построений не всегда возможно. Так если грани АSВ АSЕ явно обращены к свету, а грань ДSС находится в тени, то относительно граней ЕSД и ВSС определенный ответ можно получить только в результате соответствующих построений.

Рис. 12.22

Если тень пирамиды падает одновременно на две плоскости проекций П1 и П2, то она будет иметь излом. В этом случае необходимо вначале построить тень от вершины S, найдя действительную S2т и мнимую (S1т) тени, а затем зная точки 1 и 2, которые получим проведя прямые S1тВ1 и S1тД1, определить контур падающей тени Д11S2т2В1С1Д1 и решить вопрос об освещенности отдельных граней пирамиды.

Тени цилиндра. Чтобы построить тени поверхности цилиндра (рис. 12.23), необходимо провести к этой поверхности касательные плоскости (построение касательных плоскостей см. раздел 10.1), параллельные направлению лучей света, и найти линии касания – образующие цилиндра. Вдоль этих образующих пройдет контур собственной тени.

В частном случае, когда образующие цилиндра перпендикулярны к одной из плоскостей проекций, касательные лучевые плоскости являются проецирующими.

 

Рис. 12.23

 

Контур собственной тени цилиндра проходит вдоль образующих АК и ВL и замыкаются сверху полуокружностью АЕСДВ верхнего основания. Образующие АК и ВL найдены как линии касания к поверхности цилиндра лучевых плоскостей Р и S.

Контур падающей тени от цилиндра состоит из падающих теней образующих АК и ВL и полуокружностей АЕСДВ и АRВ. Падающие тени образующих АК и ВL определяются с помощью следов Р1 и S1, Р2 и S2 касательных лучевых плоскостей Р и S. Тени, падающие от полуокружностей АЕСДВ и АRВ, строятся, как было описано в разделе 12.4.

Решение упрощается, если тень от цилиндра падает только на одну плоскость проекций. В этом случае падающая тень верхнего основания цилиндра ограничена окружностью, проведенной из точки О1т как из центра радиусом R, равным радиусу основания цилиндра.

Тени конуса. На рис. 12.24 построены собственные и падающие тени конуса.

Рис. 12.24

 

Для построения необходимо провести к поверхности конуса касательные плоскости, параллельные лучам света, и определить линии касания. Вдоль этих линий, являющихся образующими конуса, пройдет контур собственной тени конуса. Практически построение выполняется так. Вначале определяют мнимую тень (S1т), падающую от вершины конуса на плоскость его основания П1. Затем из полученной точки проводят прямые, касательные к основанию конуса, и определяют точки касания А и В. через точки касания А и В проводят образующие конуса SА и SВ, которые вместе с дугой основания АМВ образуют контур собственной тени конуса.

Касательные S1тА и S1тВ к основанию конуса являются линиями контура падающей тени конуса. Падающая тень конуса имеет точки излома на осиХ.