Определение натуральной величины отрезка

Если отрезок прямой занимает общее положение, то ни на одной основной плоскости проекций нельзя определить его истинную длину (рис. 2.15). Построить изображение отрезка в истинную величину на комплексном чертеже можно способом прямоугольного треугольника.

Рис. 2.15

 

Возьмем отрезок АВ (АÎП₁) и построим его ортогональную проекцию на горизонтальной плоскости проекции (рис. 2.16). В пространстве при этом образуется прямоугольный треугольник А₁ВВ₁, в которой гипотенузой является сам отрезок, одним катетом – разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек её отрезка не составляет труда. То можно построить на горизонтальной проекции отрезка прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ (рис. 2.17)

Рис. 2.16 Рис. 2.17

 

 

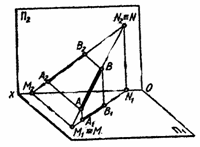
Следы прямой.

На рис. 2.18. изображен в пространстве отрезок АВ прямой общего положения. Если отрезок продлить в обе стороны от точек А и В, то в точках М и N он встретится с плоскостями проекций П₁ и П₂.

Точки пересечения прямой с плоскостями проекций называются следами прямой.

Точка М – горизонтальный след прямой, а точка N – фронтальный. Проекции следов на чертеже соответственно обозначены М₁ и М₂, N₁ и N₂. На рис. 2.19. прямая АВ и ее след изображены на комплексном чертеже.

Рис. 2.18.

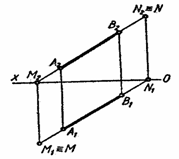
Рис. 2.19

 

Из условия, что след является точкой, одновременно принадлежащей данной прямой и плоскости проекций, вытекает правило нахождения следов прямой. Для построения на комплексном чертеже горизонтального следа прямой АВ нужно:

а) продлить фронтальную проекцию А₂В₂ до пересечения с осью Ох в точке М₂ (точка М₂ – фронтальная проекция искомого следа М);

б) провести из М₂ вертикальную линию связи до пересечения с горизонтальной проекцией А₁В₁ в точке М₁ (точка М₁ – горизонтальная проекция следа и сам след М).

Аналогично определяют горизонтальный след прямой.

 

 

2.5. Взаимное положение прямых в пространстве.

 

Две прямые в пространстве могут пересекаться, быть параллельными и скрещиваться.

2.5.1.Параллельные прямые. Если прямые в пространстве параллельны, то их одноименные проекции на любую плоскость также взаимно параллельны. Представим себе, что через параллельные прямые АВ и CD (рис. 2.20.) проведены две горизонтально проецирующие плоскости α и β, которые пересекает третья горизонтальная плоскость П₁. В результате пересечения получим параллельные между собой горизонтальные проекции А₁В₁ и С₁D₁ этих прямых. На комплексном чертеже (рис. 2.21.) изображены параллельные прямые общего положения; одноименные проекции этих прямых параллельны между собой, т.е. А₁В₁ ׀׀ С₁D₁; А₂В₂ ׀׀ С₂D₂. На рис. 2.22. параллельные прямые MN и KF лежат в плоскости, перпендикулярно к плоскости проекций П₁, а на рис. 2.23. параллельны прямые перпендикулярны к фронтальной плоскости проекций.

 

Рис. 2.20

Рис. 2.21.

 

Рис.2.22.

Рис. 2.23.

 

Для профильных прямых параллельность определяется по профильной проекции рис. 2.24.

Рис.2.24.

2.5.2. Пересекающие прямые. Если две прямые в пространстве пересекаются, то их одноименные проекции также пересекаются в точках К₁ иК₂, лежащих на общей линии связи. На рис. 2.25. изображены пересекающиеся прямые общего положения, на рис. 2.26. пересекающиеся прямые, лежащие в плоскости, перпендикулярной к плоскости проекций П₂, а на рис. 2.27. – прямые частного положения, которые пересекаются и лежат в горизонтальной плоскости.

 

 

Рис.2.25.

Рис. 2.26.

 

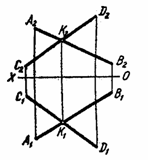
Рис. 2.27

Скрещивающиеся прямые. Если две прямые в пространстве не параллельны между собой и не пересекаются, то они скрещиваются. Точка пересечения одноименных проекций этих прямых не находятся на одной линии проекционной связи. На рис. 2.28. изображены скрещивающиеся прямые общего положения.

Рис. 2.28.

Конкурирующие точки. Определение видимости точки.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна принадлежит первой, а другая – второй из этих скрещивающихся прямых. Например, на рис точка с проекциями К₂ иК₁ принадлежит прямой АВ, а точка с проекциями L₂ и L₁ принадлежит прямой СD. Эти точки одинаково удалены от плоскости П₂, но расстояние их от плоскости П₁ различны: точка с проекциями L₂ и L₁ дальше от плоскости П₁ чем точка с проекциями К₂ иК₁ (рис 2.29.).

Рис. 2.29.

Точки с проекциями М₂, М₁ и N₂, N₁ одинаково удалены от плоскости П₁, но расстояние этих точек от плоскости П₂ различны.

Точка с проекциями L₂ и L₁ принадлежащая прямой CD, закрывает собой точку с проекциями К₂ иК₁ прямой АВ по отношению к плоскости П₂, соответствующее направление взгляда показано стрелкой у проекции L₂. По отношению к плоскости П₂ точка с проекцией N₂, N₁ прямой CD закрывает собой точку с проекциями М₂, М₁ прямой АВ; направление взгляда указано стрелкой внизу, у проекции N₁.

Точки М₂ ≡ N₂,v K₁ ≡ L₁ – называются конкурирующими и с их помощью определяется видимость.

 

 

Конкурирующие точки.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна принадлежит первой, а другая – второй из этих скрещивающихся прямых. Например, на рис точка с проекциями К₂ иК₁ принадлежит прямой АВ, а точка с проекциями L₂ и L₁ принадлежит прямой СD. Эти точки одинаково удалены от плоскости П₂, но расстояние их от плоскости П₁ различны: точка с проекциями L₂ и L₁ дальше от плоскости П₁ чем точка с проекциями К₂ иК₁ (рис 2.26.).

Рис. 2.26.

 

Определение видимости точки

Точки с проекциями М₂, М₁ и N₂, N₁ одинаково удалены от плоскости П₁, но расстояние этих точек от плоскости П₂ различны.

Точка с проекциями L₂ и L₁ принадлежащая прямой CD, закрывает собой точку с проекциями К₂ иК₁ прямой АВ по отношению к плоскости П₂, соответствующее направление взгляда показано стрелкой у проекции L₂. По отношению к плоскости П₂ точка с проекцией N₂, N₁ прямой CD закрывает собой точку с проекциями М₂, М₁ прямой АВ; направление взгляда указано стрелкой внизу, у проекции N₁.

Точки М₂ ≡ N₂,v K₁ ≡ L₁ – называются конкурирующими и с их помощью определяется видимость.