Построение тени от плоской фигуры

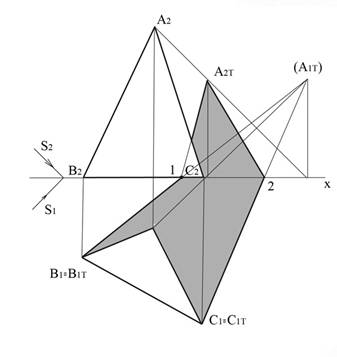
При построении падающей тени от плоской фигуры считают, что плоская фигура непрозрачна. Построение падающей тени от любой плоской фигуры сводится к построению падающих теней всех ее точек.

Рассмотрим пример построения тени плоского треугольника (рис.12.14), сторона ВС которого, лежит в горизонтальной плоскости проекций П1.В тех случаях, когда точка или прямая расположена в плоскостях проекций, задача несколько упрощается тем, что теней от этих точек и прямых строить не надо, в этом случае эти точки и прямые сами являются тенью. Для построения тени от данного треугольника надо найти тень только от точки А и соединить ее с горизонтальными проекциями точек В и С.

 

Рис.12.14 Рис.12.15

 

По общему правилу находим тень от точки А, которая падает на фронтальную плоскость проекций П2. Полученную тень А2т соединить с горизонтальными проекциями точек В и С нельзя, т.к. точки лежат в разных плоскостях проекций. Поэтому находим мнимую тень точки А на горизонтальной плоскости, предполагая, что плоскость П2 прозрачна, – точка (А1т). Найденную точку соединяем с основанием треугольника В1С1, в пересечении с осью Х находим точки преломления 1 и 2 тени треугольника, откуда тень перейдет на фронтальную плоскость проекций в точку А2т.

В следующем примере (рис.12.15) рассмотрим построение тени четырехугольника АВСД общего положения. Для построения тени этого четырехугольника необходимо построить тени от каждой его вершины. Тени от точек В – В2т и С – С2т упали на фронтальную плоскость проекций П2, а от точек А- А1т и Д – Д1т тени падают на горизонтальную плоскость проекций П1, поэтому их можно соединить между собой. Тени от точек, лежащих в разных плоскостях проекций, соединять нельзя. Поэтому тени от прямых АВ и СД будут с преломлением. Для того, чтобы найти точки преломления теней этих прямых, строим мнимые тени точек В - (В1т) и С - (С1т) на горизонтальной плоскости проекций. Соединив точку АП1т с (В1т) и Д1т с (С1т) в прямые линии находим в пересечении этих прямых с осью Х точки преломления тени 1 и 2. Фигура А1т1В2тС2т2Д1т и будет тенью четырехугольника АВСД.

Если плоская фигура параллельна плоскости проекций, на которую падает тень, то тень равна и расположена подобно самой фигуре. На рис.12.16 построена падающая тень от окружности, плоскость которой параллельна горизонтальной плоскости проекций П1. Для построения тени от этой окружности на параллельную ей плоскость достаточно построить тень от ее центра Е и провести окружность радиусом R.

 

Рис.12.16

Рис.12.17

 

На рис. 12.17 показано построение тени от окружности, расположенной параллельно фронтальной плоскости проекций. Для той части тени, которая падает на фронтальную плоскость проекций, достаточно найти тень от центра окружности и из него провести окружность радиусом равным радиусу заданной окружности. Та тень, которая падает на горизонтальную плоскость проекций, будет изображаться в виде эллипса. Для построения этой части тени окружность разбивают на 8 или 10 частей и строят тени этих точек, затем плавно соединяют эти точки.

 

МЕТОД ОБРАТНЫХ ЛУЧЕЙ

 

На рис. 12.18 даны плоская фигура АВС и отрезок ДЕ. Необходимо построить тень отрезка ДЕ на плоскость треугольника АВС. При построении можно воспользоваться методом обратного луча. Для этого предварительно построим тень от треугольника АВС на горизонтальную плоскость проекций П1. Вслед за этим строим тень на горизонтальную плоскость проекций от отрезка ДЕ. В точке Fт тень от прямой пересекается с тенью от стороны треугольника АС. В точке Rт продолжение тени от отрезка ДЕ пересекается с тенью от стороны ВС. Проведем из точек F1т и R1т лучи света в обратном направлении до пересечения с соответствующими сторонами треугольника в точках Fт и Rт. Через эти точки проходит тень от прямой ДЕ на плоскости АВС. Отметим пересечение этой линии с лучом света, проходенным через точку Е. Отметим пересечение этой линии с лучом света, проходящим через точку Е.

 

Рис. 12.18

 

Освещенность отсека плоскости. Определим освещенность самого треугольника АВС. Для этого воспользуемся конкурирующими точками N и G (точка G принадлежит лучу света, проходящему через точку Е, а точка N - стороне АВ). При взгляде спереди точка G ближе к зрителю, следовательно, лучи света падают на треугольник со стороны зрителя и он видит освещенную сторону треугольника. Возьмем конкурирующие точки на луче (V) и на стороне АВ (L). При взгляде сверху мы вначале видим точку L, а затем уже точку V. Следовательно, лучи падают на плоскость треугольника с противоположной относительно зрителя стороны плоскости, и мы видим ее неосвещенную сторону.

Следовательно, чтобы проверить освещенность плоской фигуры, следует провести лучи света и, взяв конкурирующие точки на луче (до его пересечения с плоскостью) и одной из линий фигуры, установить, что ближе к зрителю – луч или линия. Если ближе луч, то фигура освещена, и наоборот.