Пространственная (или декартовая) система координат. Плоскости проекций

ГЛАВА 1

Проекции точки.

1.1. Метод проецирования.

Для построения изображения предметов на плоскости пользуютсь методом проецирования. Слово «проекция» - латинское, от глагола projecere, что в переводе означает «бросать вперед».

Следовательно, проекция – это изображение предмета, «отброшенное» на плоскость при помощи лучей. Спроецировать предмет на плоскость – это значит построить его изображение на плоскости.

Проекции разделяются на центральные и параллельные.

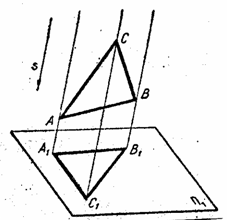
Рис. 1.1.

1.1.1. Идея центрального проецирования видна из рис. 1.1. Пусть заданы в пространстве точка S – центр проекции и плоскости. П₁ – плоскость проекции. Плоскость П₁ и точка S составляют аппарат центральной проекции. Проецируемый треугольник АВС называется оригиналом, или натурой. Чтобы спроецировать заданный оригинал, нужно из центра проекции S через вершины треугольника провести проецирующие лучи до пересечения с плоскостью проекции П₁. Точки пересечения А₁, В₁, С₁, называются центральными проекциями вершин А, В, С, на плоскость П₁, а треугольник А₁В₁С₁ – центральной проекции треугольника АВС. Центральные проекции (перспективу) применяют в архитектурных чертежах, в аэрофотосъемке, рисовании и др. Вследствие трудностей при построении изображений и их измерении, а также при чтении чертежей, в машиностроительном черчении центральными проекциями не используются.

1.1.2. В начертательной геометрии используют метод параллельного проецирования (рис. 1.2.). Как и в предыдущем случае, выбирают плоскость проецирования П₁, но вместо центра проекции S задают направление проецирования s, т. е. считают, что точка S – центр проекции – расположена в бесконечности и поэтому проецирующие лучи параллельны между собой. Плоскость П₁ и направление s составляют аппарат параллельной проекции. Чтобы спроецировать треугольник АВС на плоскость П₁, через вершины А, В, С проводят проецирующие лучи параллельно направлению проецирования s. Треугольник А₁В₁С₁, образованный пересечением лучей АА₁, ВВ₁, СС₁ с плоскостью П₁, и будет параллельной проекцией треугольника АВС.

Рис. 1.2.

Параллельные проекции разделяются на прямоугольные и косоугольные. Если проецирующие углы перпендикулярны к плоскости проекций (рис. 1.3.), то способ проецирования называется прямоугольным, а полученные при этом проекции – прямоугольными, или ортогональными. Если же угол наклона лучей не равен 90º, то подобная параллельная проекция называется косоугольной. В черчении используют, главным образом, прямоугольные проекции.

Рис. 1.3.

 

 

1.2. Задание точки н комплексном чертеже Монжа (эпюр Монжа)

 

1.2.1. Пространственная (или декартовая) система координат. Плоскости проекций

1.2.2 Проецирование точки на две плоскости проекций. Четверти пространства

1.2.3 Проекции точки на три плоскости проекций. Октанты пространства

1.2.4 Точки проекций общего и частного положения

 

 

Обратимость чертежа

 

Обратимость чертежа. Проецированием на одну плоскость проекций получается изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А₁ (см. рис. 1.4.) не определяет положение самой точки в пространстве, так как неизвестно, на какое расстояние она удалена от плоскости проекций П₁. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображения дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа.

ГЛАВА 2

Проекции прямой.

 

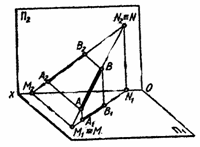
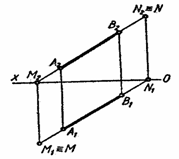
Следы прямой.

На рис. 2.18. изображен в пространстве отрезок АВ прямой общего положения. Если отрезок продлить в обе стороны от точек А и В, то в точках М и N он встретится с плоскостями проекций П₁ и П₂.

Точки пересечения прямой с плоскостями проекций называются следами прямой.

Точка М – горизонтальный след прямой, а точка N – фронтальный. Проекции следов на чертеже соответственно обозначены М₁ и М₂, N₁ и N₂. На рис. 2.19. прямая АВ и ее след изображены на комплексном чертеже.

Рис. 2.18.

Рис. 2.19

 

Из условия, что след является точкой, одновременно принадлежащей данной прямой и плоскости проекций, вытекает правило нахождения следов прямой. Для построения на комплексном чертеже горизонтального следа прямой АВ нужно:

а) продлить фронтальную проекцию А₂В₂ до пересечения с осью Ох в точке М₂ (точка М₂ – фронтальная проекция искомого следа М);

б) провести из М₂ вертикальную линию связи до пересечения с горизонтальной проекцией А₁В₁ в точке М₁ (точка М₁ – горизонтальная проекция следа и сам след М).

Аналогично определяют горизонтальный след прямой.

 

 

2.5. Взаимное положение прямых в пространстве.

 

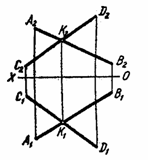
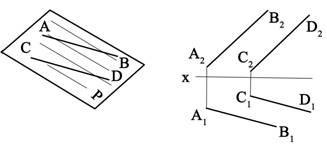
Две прямые в пространстве могут пересекаться, быть параллельными и скрещиваться.

2.5.1.Параллельные прямые. Если прямые в пространстве параллельны, то их одноименные проекции на любую плоскость также взаимно параллельны. Представим себе, что через параллельные прямые АВ и CD (рис. 2.20.) проведены две горизонтально проецирующие плоскости α и β, которые пересекает третья горизонтальная плоскость П₁. В результате пересечения получим параллельные между собой горизонтальные проекции А₁В₁ и С₁D₁ этих прямых. На комплексном чертеже (рис. 2.21.) изображены параллельные прямые общего положения; одноименные проекции этих прямых параллельны между собой, т.е. А₁В₁ ׀׀ С₁D₁; А₂В₂ ׀׀ С₂D₂. На рис. 2.22. параллельные прямые MN и KF лежат в плоскости, перпендикулярно к плоскости проекций П₁, а на рис. 2.23. параллельны прямые перпендикулярны к фронтальной плоскости проекций.

 

Рис. 2.20

Рис. 2.21.

 

Рис.2.22.

Рис. 2.23.

 

Для профильных прямых параллельность определяется по профильной проекции рис. 2.24.

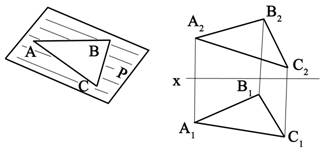
Рис.2.24.

2.5.2. Пересекающие прямые. Если две прямые в пространстве пересекаются, то их одноименные проекции также пересекаются в точках К₁ иК₂, лежащих на общей линии связи. На рис. 2.25. изображены пересекающиеся прямые общего положения, на рис. 2.26. пересекающиеся прямые, лежащие в плоскости, перпендикулярной к плоскости проекций П₂, а на рис. 2.27. – прямые частного положения, которые пересекаются и лежат в горизонтальной плоскости.

 

 

Рис.2.25.

Рис. 2.26.

 

Рис. 2.27

Скрещивающиеся прямые. Если две прямые в пространстве не параллельны между собой и не пересекаются, то они скрещиваются. Точка пересечения одноименных проекций этих прямых не находятся на одной линии проекционной связи. На рис. 2.28. изображены скрещивающиеся прямые общего положения.

Рис. 2.28.

Конкурирующие точки. Определение видимости точки.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна принадлежит первой, а другая – второй из этих скрещивающихся прямых. Например, на рис точка с проекциями К₂ иК₁ принадлежит прямой АВ, а точка с проекциями L₂ и L₁ принадлежит прямой СD. Эти точки одинаково удалены от плоскости П₂, но расстояние их от плоскости П₁ различны: точка с проекциями L₂ и L₁ дальше от плоскости П₁ чем точка с проекциями К₂ иК₁ (рис 2.29.).

Рис. 2.29.

Точки с проекциями М₂, М₁ и N₂, N₁ одинаково удалены от плоскости П₁, но расстояние этих точек от плоскости П₂ различны.

Точка с проекциями L₂ и L₁ принадлежащая прямой CD, закрывает собой точку с проекциями К₂ иК₁ прямой АВ по отношению к плоскости П₂, соответствующее направление взгляда показано стрелкой у проекции L₂. По отношению к плоскости П₂ точка с проекцией N₂, N₁ прямой CD закрывает собой точку с проекциями М₂, М₁ прямой АВ; направление взгляда указано стрелкой внизу, у проекции N₁.

Точки М₂ ≡ N₂,v K₁ ≡ L₁ – называются конкурирующими и с их помощью определяется видимость.

 

 

Конкурирующие точки.

Как надо рассматривать точку пересечения одноименных проекций скрещивающихся прямых? Она представляет собой проекции двух точек, из которых одна принадлежит первой, а другая – второй из этих скрещивающихся прямых. Например, на рис точка с проекциями К₂ иК₁ принадлежит прямой АВ, а точка с проекциями L₂ и L₁ принадлежит прямой СD. Эти точки одинаково удалены от плоскости П₂, но расстояние их от плоскости П₁ различны: точка с проекциями L₂ и L₁ дальше от плоскости П₁ чем точка с проекциями К₂ иК₁ (рис 2.26.).

Рис. 2.26.

 

Определение видимости точки

Точки с проекциями М₂, М₁ и N₂, N₁ одинаково удалены от плоскости П₁, но расстояние этих точек от плоскости П₂ различны.

Точка с проекциями L₂ и L₁ принадлежащая прямой CD, закрывает собой точку с проекциями К₂ иК₁ прямой АВ по отношению к плоскости П₂, соответствующее направление взгляда показано стрелкой у проекции L₂. По отношению к плоскости П₂ точка с проекцией N₂, N₁ прямой CD закрывает собой точку с проекциями М₂, М₁ прямой АВ; направление взгляда указано стрелкой внизу, у проекции N₁.

Точки М₂ ≡ N₂,v K₁ ≡ L₁ – называются конкурирующими и с их помощью определяется видимость.

Глава 3

 

Проекции плоскости

3.1 Способы задания плоскости на эпюре

 

Из курса элементарной геометрии известно, что через три точки не лежащие на одной прямой можно провести плоскость и при том только одну. Таким образом, положение плоскости в пространстве логично определить (задать) тремя точками (точки А, В, С, табл. 3.1, п1.)

Кроме этого, положение плоскости в пространстве определяют: прямая АВ и точка С, не лежащая на прямой (табл. 3.1, п.2), две пересекающиеся прямые АВ и CD (табл. 3.1, п.3), две параллельные прямые АВ и CD (табл. 3.1, п.4), плоская фигура, т.е. часть плоскости, ограниченная линиями (треугольник, квадрат, круг, ромб и т.д.).

На эпюре (табл. 3.1) плоскость может быть задана соответственно проекциями трех точек, не лежащих на одной прямой, прямой и точки, не лежащей на прямой, двух пересекающихся или параллельных прямых, проекцией плоской фигуры.

Плоскости условимся обозначать прописными латинскими буквами, следующими за буквой P по алфавиту: R, S, T и т.д.

 

Таблица 3.1 Способы задания плоскости в пространстве и на эпюре

№	Задание плоскости в пространстве	Наглядное изображение	Эпюр	Задание плоскости на эпюре
	Тремя точками, не лежащими на одной прямой		Проекциями трех точек, не лежащих на одной прямой
	Прямой и точкой, не лежащей на прямой		Проекциями прямой и точки, не лежащими на одной прямой
	Двумя пересекающимися прямыми		Проекциями двух пересекающихся прямых
	Двумя параллельными прямыми		Проекциями двух параллельных прямых
	Плоской фигурой		Проекциями плоской фигуры
	Следами		Следами

 

 

3.2 Следы плоскости

 

Положение плоскости в пространстве может быть определено ее следами. Следами плоскости называются прямые линии, по которым данная плоскость пересекается с плоскостями проекций.

В общем случае плоскость имеет три следа – горизонтальный, фронтальный и профильный.

На рис. 3.1. и в таблице 3.1. п.6 они обозначены соответственно P₁, P₂, P₃ (буквой Р обозначена заданная плоскость, а индексы 1, 2, 3 означают, с какой из плоскостей проекций пересекается плоскость Р).

В точках P_x, P_y, P_z, лежащих на осях координат, следы плоскости пересекаются. Эти точки называются точками схода следов плоскости.

Следы плоскости всегда можно построить, если положение плоскости в пространстве задано одним из перечисленных выше способов.

Если прямая АВ (рис.3.1. а и б) лежит в плоскости Р, то она пересечет плоскость П₁ в точке М₁ расположенной на линии Р₁, т.е. горизонтальный след прямой, лежащей в плоскости, расположен на горизонтальном следе плоскости.

 

 

Рис. 3.1.

 

Плоскость П₂ прямая АВ пересечет в точке N, расположенной на линии Р₂.

Иными словами, следы прямой, лежащей в плоскости, расположены на одноименных следах плоскости.

Отсюда следует, что следы плоскости должны проходить через одноименные следы прямых, лежащих в плоскости.

Чтобы построить след плоскости, необходимо определить следы двух прямых, лежащих в плоскости.

На рис. 3.1. плоскость задана двумя пересекающимися прямыми АВ и СD. Чтобы построить горизонтальный след плоскости необходимо найти горизонтальный след прямой АВ – точку М и прямой СD – точку М¹. Горизонтальный след плоскости будет проходить через точки М и М¹.

Фронтальный след плоскости Р₂ строится аналогично. Следует отметить, что для построения следа Р₂ достаточно иметь фронтальный след только одной прямой, так как второй точкой, определяющей положение следа Р₂ будет точка Р_х схода следов (точка пересечения ранее построенного следа Р₁ с осью х).

 

 

Главные линии плоскости

 

В плоскости можно расположить бесчисленное количество прямых, среди которых будут линии уровня плоскости, т.е. прямые, параллельные плоскостям проекций, и прямые, перпендикулярные к этим линиям уровня, так называемые линии наибольшего уклона плоскости. Такие прямые называются главными (или особыми) линиями плоскости. К первым относятся горизонтальные линии плоскости (горизонтали плоскости), а также фронтальные и профильные (фронтали плоскости, профильные прямые плоскости).

Главные линии плоскости имеют большое практическое применение. Например при помощи горизонталей изображаются части поверхности земляных сооружений, ограниченные плоскостями (откосы насыпей и выемок, плотин и т.п.), определяются их контуры на планах и т.д. Горизонталями плоскости – напластования горных пород, ориентируется положение пласта породы по отношению к сторонам света (простирание), а линией наибольшего уклона указывается положение этого пласта по отношению к плоскости горизонта (падение).

Горизонтали и фронтали плоскости широко используются при решении различных задач начертательной геометрии. Задание плоскости этими линиями имеет ряд преимуществ перед другими способами задания её.

Горизонтали плоскости. Горизонтальными линиями уровня плоскости называются прямые, лежащие в этой плоскости и параллельные горизонтальной плоскости проекций.

 

Рис. 3.3

 

Горизонтальную линию уровня любой плоскости можно рассматривать как линию пересечения этой плоскости с горизонтальной плоскостью уровня. Горизонтальную плоскость проекций П₁ можно принять за горизонтальную плоскость нулевого уровня. Поэтому горизонтальный след Р₁ плоскости можно принять за горизонтальную линию нулевого уровня этой плоскости.

Все горизонтали плоскости, в том числе её горизонтальный след взаимно параллельны как линии пересечения одной плоскости с параллельными плоскостями уровня.

На рис. 3.3, а изображена плоскость Р, заданная следами Р₁ и Р₂, горизонталь h и ее проекции h₁ и h₂. Для построения проекций горизонтали на комплексном чертеже (рис. 3.3, б) проведена проекция h₂||ОХ, построены проекции N₂=h₂ÇP₂ и N₁ÎОХ фронтального следа N горизонтали и через N₁ проведена проекция h₁||P₁. Построенная горизонталь h находится в плоскости Р, так как она проходит через точку NÎP и параллельна прямой Р₁ÎР.

На рис.3.3, в показана горизонталь А1, построенная в плоскости треугольника АВС.

Фронтали плоскости. Фронтальными линиями уровня плоскости называются прямые, лежащие в этой плоскости и параллельные фронтальной плоскости проекций.

Проведя рассуждения, аналогичные рассмотренным для горизонтали, придем к выводу, что фронтали плоскости параллельны фронтальному следу Р₂ плоскости, являющемуся фронтальной линией нулевого уровня этой плоскости.

Плоскость Р, заданная следами Р₁ и Р₂, фронталь f и её проекции f₁ и f₂ изображены на рис 3.4, а.

рис 3.4

 

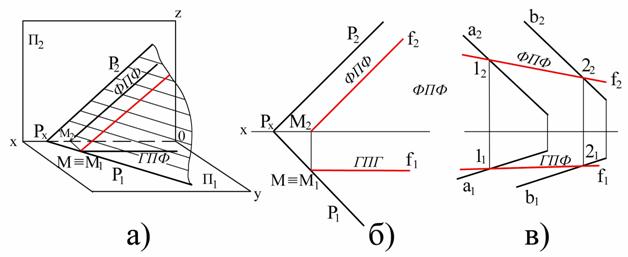
Для построения проекций фронтали на комплексном чертеже (рис 3.4, б) проведена проекция f₁||ОХ, построены проекции М₁=f₁ÇР₁ и М₁ÎОХ горизонтального следа М фронтали и через М₂ проведена проекция f₂||Р₂. Построенная фронталь fÎР, т.к. она проходит через точку МÎР и параллельна прямой Р₂ÎР.

Линия наибольшего уклона (ската) плоскости.

Из всех линий, расположенных в плоскости, прямая, идущая под прямым углом к горизонталям (рис. 3.5,а), наклонена к плоскости П₁ под наибольшим углом – линия наибольшего ската плоскости (ЛНС). Её горизонтальная проекция составляет прямой угол с горизонтальным следом плоскости и с горизонтальными проекциями горизонталей. Поэтому ЛНС следует начинать строить с горизонтальной проекции (рис. 3.5, б), которая расположена по прямым углом к следу Р₁ и к горизонтальной проекции горизонтали. Отметив на горизонтальной проекции линии наибольшего ската две точки М₁ и А₁, строим их фронтальные проекции. Фронтальная проекция линии наибольшего ската пройдет через точки М₂ и А₂. Построение линии наибольшего ската на плоскости, заданной треугольником АВС, показано на рис. 3.5, в, где сначала перпендикулярно к горизонтальной проекции горизонтали проведена горизонтальная проекция 1₁-2₁, а затем фронтальная проекция 1₂-2₂ этой линии.

Угол a наклона линии наибольшего ската к плоскости П₁ определяет наклон плоскости Р к плоскости П_!.

 

Рис. 3.5

 

Параллельность плоскостей

 

Рассмотрим случай взаимной параллельности плоскостей. Если плоскости параллельны, то всегда в каждой из них можно построить по две пересекающиеся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости (рис. 3.17,а).

 

Рис. 3.17

 

Это служит основным признаком для определения, параллельны плоскости между собой или не параллельны. Такими прямыми могут служить, например, следы обеих плоскостей: если два пересекающихся между собой следа одной плоскости параллельны одноименным с ними следам другой плоскости, то обе плоскости параллельны между собой (3.17, б, где Р₁||Q₁, P₂||Q₂).

На рис. 3.18 показано построение плоскости, параллельной заданной плоскости Р.

В первом случае (рис. 3.18,а) искомая плоскость задана двумя пересекающимися прямыми, проходящими через точку А и являющимися главными линиями плоскости – горизонталью и фронталью. На рис. 3.18 б показано построение следов искомой плоскости Т, проходящей через заданную точку А.

Решение начато с построения горизонтали искомой плоскости и её фронтального следа N, через который проведен фронтальный лед плоскости Т(Т₁,Т₂). Через точку схода следов Т_х прошел горизонтальный след искомой плоскости Т₁||Р₁.

 

Рис. 3.18

 

Примеры позиционных и метрических задач на плоскость

 

Пример 1. В плоскости, заданной треугольником АВС, построить точку D (рис. 3.21).

Решение.

1. Необходимо в данной плоскости провести прямую. Зададим для этого две точки, заведомо лежащие в данной плоскости. Одной из таких точек может быть вершина А(А₁;А₂) треугольника. Вторую точку Е(Е₁;Е₂) зададим на стороне ВС. Через одноименные проекции А₁ и Е₁, А₂ и Е₂ проведем прямые. Эти прямые являются проекциями прямой. Лежащей в данной плоскости.

2. На построенной прямой АЕ зададим точку D. Для этого построим D₁ÎА₁Е₁ и D₂ÎА₂Е₂. Точка D лежит в заданной плоскости, т.к.к она принадлежит прямой АЕ, лежащей в этой плоскости

 

Рис. 3.21

 

Пример 2. Построить линию наибольшего уклона плоскости, заданной параллельными прямыми а(а₁; а₂) и b(b₁; b₂) и определить угол a между этой плоскостью и горизонтальной плоскостью проекций (рис. 3.22)

 

Рис. 3.22

 

Решение

1. Проведем горизонталь h данной плоскости (см. гл.3 рис. 3.3, в). Проекциями этой горизонтали будут прямые h₁ и h₂.
2. Проведем прямую, перпендикулярную к горизонтальной проекции горизонтали, и отметим точки С₁ - пересечения её с h₁ D₁ – са₁. Прямая С₁D₁ является горизонтальной проекцией линии наибольшего ската.
3. Построим фронтальные проекции С₂ и D₂. Для этого из С₁ и D₁ проведем вертикальные линии связи до пересечения соответственно с h₂ и а₂.
4. Прямая, соединяющая точки С₂ и D₂, является фронтальной проекцией линии наибольшего уклона.
5. Угол a определяем из прямоугольного треугольника D₁C₁E₀, построенного на С ₁D₁ как на катете. Второй катет D₀D₁ = E₂D₂. Искомый угол a=ÐD₀C₁D₁

 

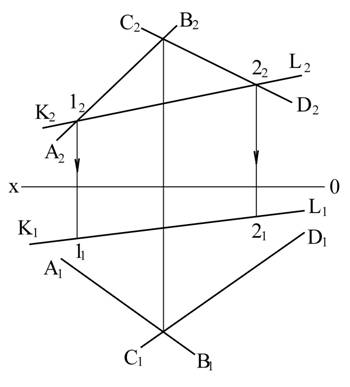
Пример 3. Задана плоскость пересекающимися прямыми АВ и CD. Определить лежит ли прямая KL в этой плоскости.

 

Рис. 3.23

 

Решение.

1. Обозначим точки пересечения фронтальных проекций прямых АВ и KL через 1₂ и прямых CD и KL через 2₂.

2. Строим их горизонтальные проекции – точки 1₁ и 2₂ на горизонтальной проекции (K₁L₁) прямой KL. Из построения видно, что точки 1(1₁1₂) и 2(2₁2₂) прямая KL на заданной плоскости не лежат. Следовательно, прямая KL в плоскости не лежит. Решение этой задачи можно начать и с пересечения горизонтальных проекций.

 

Пример 4. В плоскости, заданной двумя параллельными прямыми АВ и CD, провести фронталь на расстоянии 15 мм от фронтальной плоскости проекций (рис. 3.24)

Рис. 3.24

 

Решение. Проводим на расстоянии 15 мм от оси проекций параллельную ей горизонтальную проекцию (1₁-2₂) фронтали, которая пересекает прямые А₁В₁ и C₁D₁ в точках 1₁ и 2₂.

Затем находим точки 1₁ и 2₂ на прямых А₂В₂ и C₂D₂ и проводим через них фронтальную проекцию (1₂2₂) фронтали.

 

Пример 5. Найти прямую пересечения плоскостей Р и Q.

 

Рис. 3.25

 

Решение. Плоскость Р и Q пересекаются по прямой общего положения, проходящей через точку-след (М₁;М₂) пересечения горизонтальных следов плоскостей. Точка-след (N₁;N₂) пересечения фронтальных следов плоскостей недоступна, т.к. эти следы плоскостей по заданию, в пределах чертежа не пересекаются.

Вместо точки (N₁;N₂) необходимо найти другую произвольную точку прямой пересечения, общую для заданных плоскостей. Для этого вводим вспомогательную плоскость R, например параллельную П которая, как известно, пересекает каждую из данных плоскостей по горизонтали. На их пересечении получаем вспомогательную точку (К₁;К₂), общую для данных плоскостей. Найдя эту вторую точку (К₁;К₂) прямой, проводим её проекцию: горизонтальную – через точки М₁ и К₁ и фронтальную через точки М₂ и К₂.

 

Пример 6. Найти точку пересечения прямой АВ с плоскостью Р (рис. 3.26)

 

Рис. 3.26

 

Решение. Обозначим искомую точку через точку К. Так как точка К (К₁;К₂) лежит на профильно-проецирующей плоскости. То её профильная проекция (К₃) должна лежать на профильном следе (Р₃) плоскости. Вместе с тем, так как эта же точка лежит и на прямой АВ, то её профильная проекция (К₃) должна лежать так же где-то на профильной проекции (А₃В₃) прямой. Следовательно искомая точка должна лежать на их пересечении. Найдя профильный след плоскости и профильную проекцию прямой, получаем на их пересечении профильную проекцию (К₃) искомой точки. Зная профильную проекцию (К₃) искомой точки, находим две другие её проекции на одноименных проекциях прямой.

 

Пример 7. Даны плоскость Р и точка А. Определить расстояние то точки до плоскости (рис. 3.27)

 

 

Рис. 3.27

 

Решение. Опускаем из точки А (А₁;А₂) перпендикуляр на плоскость Р и находим его основание на этой плоскости, для чего ищем точку К (К₁;К₂) пересечения перпендикуляра с плоскостью. Имея проекции (А₁К₁;А₂К₂) отрезка перпендикуляра, определим его действительную величину методом прямоугольного треугольника.

 

Пример 8. Даны треугольник АВС и точка К. Определить расстояние между ними. (рис. 3.28)

 

Рис. 3.28

 

Решение. Опускаем из заданной точки Е (Е₁;Е₂) перпендикуляр на плоскость треугольника: К₁Е₁ перпендикулярно горизонтальной проекции горизонтали (К₁Е₁^С₁F₁), К₂Е₂ перпендикулярно фронтальной проекции фронтали (К₂Е₂^А₂ D₂). Находим точку пересечения перпендикуляра с плоскостью треугольника (К₁;К₂), определяем натуральную величину отрезка перпендикуляра (К₁Е₁;К₂Е₂) методом прямоугольного треугольника.

 

Глава 4

Методы преобразования комплексного чертежа (эпюра Монжа)

4.1. Четыре основных задачи на преобразование

 

При разработке чертежей объектов необходимо давать наиболее выгодное изображение объекта в целом или его исследуемых элементов. Этого можно достичь, если прямые линии, плоские фигуры (основания, грани, ребра, оси) геометрических тел находятся в частном положении, чего можно достигнуть путем построения новых дополнительных проекций, исходя из двух заданных. Эти дополнительные проекции дают либо вырожденные проекции отдельных элементов, либо эти элементы в натуральную величину. Так вот построение дополнительных проекций называют преобразованием эпюра (чертежа).

Четыре основных задачи на преобразования.

1. Определение величины отрезка АВ общего положения;
2. Приведение отрезка прямой общего положения в проецирующее положение;
3. Приведение плоской фигуры общего положение в проецирующее положение;
4. Определение натурального вида плоской фигуры.

Кроме указанных выше задач указанным методом можно определить расстояние между двумя скрещивающимися прямыми.

Преобразование эпюра может быть выполнено следующими методами:

1. заменой плоскостей проекций;
2. плоскопараллельным перемещением;
3. вращением вокруг линий уровня;
4. совмещением.

Рассмотрим эти методы подробно.

 

 

Глава 5

Многогранники

 

5.1. Задание многогранников на эпюре Монжа (общие положения)

Многие пространственные фигуры представлены в виде многогранников – замкнутых пространственных фигур, ограниченных плоскими многоугольниками. Вершины и стороны многоугольников являются вершинами и ребрами многогранника, при этом, если все его вершины и ребра находятся по одну сторону плоскости любой из его граней, то многогранник называется выпуклым, а все его грани являются выпуклыми многоугольниками.

Многогранники широко распространены в архитектуре, строительстве, технике. Многие детали машин и механизмов, станков, инструментов и приборов имеют форму многогранников или их сочетаний.

 

 

Виды многогранников

 

Наибольший практический интерес представляют призмы, пирамиды и выпуклые однородные многогранники – тела Платона (тетраэдр, гексаэдр, октаэдр, додекаэдр и икосаэдр). Это правильные (соответственно) четырех-, шести-, восьми-, двенадцати- и двадцатигранники.

Пирамида – это многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной (рис. 5.1). Пирамида называется правильной, если основанием её является правильной многоугольник, а высота (перпендикуляр, опущенный из вершины на основание) проходит через центр этого многоугольника.

 

Рис. 5.1

 

Пирамида называется усечённой, если вершина её отсекается плоскостью, пересекающей все ребра, исходящие из этой вершины (рис. 5.1, 5.2).

 

 

Рис. 5.2

 

Призмой называют многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы (рис. 5.3).

 

Рис. 5.3

 

Призму называют прямой, если ребра её перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, а боковые рёбра перпендикулярны основанию, то её называют параллелепипедом (рис. 5.4)

 

Рис. 5.4

 

Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными (это – тела Платона).

Русский математик Леонард Эйлер открыл и доказал знаменитую теорему, связывающую число граней (Г), вершин (В) и рёбер (Р) любого выпуклого многогранника:

Г + В – Р = 2 (число Эйлера)

Построение проекций многогранника сводиться к построению проекций вершин и рёбер, т.е. сетки многогранника.

 

Рисунок 8.7

 

Если секущая плоскость занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (на рис. 8.8 б – на фронтальной), окружность сечения изображается отрезком прямой (1₂ - 4₂), длина которого равна диаметру окружности, а на другой плоскости - эллипсом, большая ось которого (5₁ -6₁) равна диаметру окружности сечения. Этот эллипс строят по точкам. Точки видимости 2 и 3 относительно плоскости П₁ лежат на экваторе сферы.

Рисунок 8.8

 

Построить проекции линии пересечения плоскость Т с поверхностью цилиндра.

Проводим через ось цилиндра горизонтально – проецирующую плоскость R₁ перпендикулярную к плоскости Т₁ плоскость R пересекает поверхность цилиндра по образующим, а плоскость Т – по прямой (N₁M₁;N₂M₂); на их пересечении получаем низшую точку (1) и высшую точку (2) линий пересечения. Проводим через ось цилиндра плоскость R₁, параллельную вертикальной плоскости проекций; плоскость R₁ пересекает поверхность цилиндра по крайним образующим, а плоскость Т – по фронтали; на их пересечении получаем точки (3₁; 3₂) (4₁; 4₂) линии пересечения.

Находим точки пересечения профильных образующих цилиндра с плоскостью Т. Горизонтальные проекции (5) и (6) этих точек известны; по ним пользуясь горизонталями, находим вертикальные проекции (5.2 и 6.2). Аналогично находим точки пересечения еще нескольких образующих цилиндра с плоскостью. Соединив последовательно вертикальные проекции всех найденных точек, получаем вертикальную проекцию линии пересечения – эллипс.

 

Рисунок 8.9

 

Построение проекции линии пересечения плоскости Т с поверхностью конуса.

 

Построить проекции линии пересечения плоскости Т с поверхностью конуса.(рис. 8.10).

Плоскость Т пересекает поверхность конуса по эллипсу, вертикальная проекция которого совпадает с вертикальным следом (Т₂) плоскости. Горизонтальную проекцию эллипса строим по точкам: задаем вертикальные проекции ряда его точек и находим их горизонтальные проекции. Затем через горизонтальные проекции точек проводим кривую – эллипс. Горизонтальную проекцию линии пересечения, как эллипс, можно построить так же по главным осям: по большой оси и по малой оси. Истинную величину эллипса можно построить по двум его главным осям: по большой оси и по малой оси, которую находят по вертикальной проекции.

 

Рисунок 8.10

Построить линии проекции плоскости Т с поверхностью шара (сферы).

 

Проводим через центр шара горизонтально – проектирующую плоскость R перпендикулярную к плоскости Р; плоскость R пересекает поверхность шара по окружности, а плоскость Т - по прямой (N₁M₁; N₂M₂); на пересечении получаем низшую точку (1) и высшую точку (2) линий пересечения.

Для того чтобы найти промежуточные точки линий пересечений, проводим между точками (1) и (2) ряд вспомогательных плоскостей Q, Q₁ и т. д., параллельных горизонтальной плоскости проекций. Например, плоскость Q₂₁ пересекает поверхность шара по окружности, а плоскость Т – по горизонтали; на их пересечении получаем две точки: (3) и (4) и т. д.

Для того чтобы на вертикальной проекции кривой отделить видимую ее часть от невидимой, проводим через центр шара плоскость R1, параллельную вертикальной плоскости проекций; плоскость R₁ пересекает поверхность шара по главному меридиану, а плоскость Т по фронтали. На их пересечении получаем точки (1) и (2). Для того что бы на горизонтальной проекции кривой отделить в