Теорема о проецировании прямого угла.

1. Если плоскость, в которой расположен некоторый угол, перпендикулярна к плоскости проекций, то он проецируется на эту плоскость проекций в виде прямой линии.

2. Если плоскость прямого угла не перпендикулярна к плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла.

Рис. 2.30.

Положим, что сторона ВС прямого угла АВС (рис. 2.30.) параллельна плоскости проекций. В таком случае прямая СВ параллельна С₁В₁. Пусть вторая сторона (АС) прямого угла пересекает свою проекцию А₁С₁ в точке К. Проводим в плоскости проекций через точку К прямую параллельно С₁В₁. Прямая KL так же параллельна СВ, и угол CKL получается прямым. Согласно тереме о трех перпендикулярах угол С₁KL также прямой. Следовательно, и угол А₁С₁В₁ прямой.

Рис. 2.31.

Этой теореме о проецировании прямого угла соответствуют две обратных.

3. Если проекция плоскости угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций. (рис. 2.31.).

4. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой.

5. Если стороны угла одинаково наклонены к плоскости проекций, то угол не может равняться проектируемому углу.

 

Глава 3

 

Проекции плоскости

3.1 Способы задания плоскости на эпюре

 

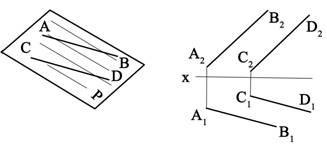
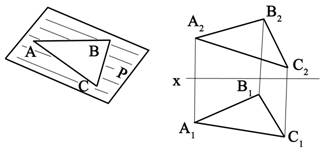
Из курса элементарной геометрии известно, что через три точки не лежащие на одной прямой можно провести плоскость и при том только одну. Таким образом, положение плоскости в пространстве логично определить (задать) тремя точками (точки А, В, С, табл. 3.1, п1.)

Кроме этого, положение плоскости в пространстве определяют: прямая АВ и точка С, не лежащая на прямой (табл. 3.1, п.2), две пересекающиеся прямые АВ и CD (табл. 3.1, п.3), две параллельные прямые АВ и CD (табл. 3.1, п.4), плоская фигура, т.е. часть плоскости, ограниченная линиями (треугольник, квадрат, круг, ромб и т.д.).

На эпюре (табл. 3.1) плоскость может быть задана соответственно проекциями трех точек, не лежащих на одной прямой, прямой и точки, не лежащей на прямой, двух пересекающихся или параллельных прямых, проекцией плоской фигуры.

Плоскости условимся обозначать прописными латинскими буквами, следующими за буквой P по алфавиту: R, S, T и т.д.

 

Таблица 3.1 Способы задания плоскости в пространстве и на эпюре

№	Задание плоскости в пространстве	Наглядное изображение	Эпюр	Задание плоскости на эпюре
	Тремя точками, не лежащими на одной прямой		Проекциями трех точек, не лежащих на одной прямой
	Прямой и точкой, не лежащей на прямой		Проекциями прямой и точки, не лежащими на одной прямой
	Двумя пересекающимися прямыми		Проекциями двух пересекающихся прямых
	Двумя параллельными прямыми		Проекциями двух параллельных прямых
	Плоской фигурой		Проекциями плоской фигуры
	Следами		Следами

 

 

3.2 Следы плоскости

 

Положение плоскости в пространстве может быть определено ее следами. Следами плоскости называются прямые линии, по которым данная плоскость пересекается с плоскостями проекций.

В общем случае плоскость имеет три следа – горизонтальный, фронтальный и профильный.

На рис. 3.1. и в таблице 3.1. п.6 они обозначены соответственно P₁, P₂, P₃ (буквой Р обозначена заданная плоскость, а индексы 1, 2, 3 означают, с какой из плоскостей проекций пересекается плоскость Р).

В точках P_x, P_y, P_z, лежащих на осях координат, следы плоскости пересекаются. Эти точки называются точками схода следов плоскости.

Следы плоскости всегда можно построить, если положение плоскости в пространстве задано одним из перечисленных выше способов.

Если прямая АВ (рис.3.1. а и б) лежит в плоскости Р, то она пересечет плоскость П₁ в точке М₁ расположенной на линии Р₁, т.е. горизонтальный след прямой, лежащей в плоскости, расположен на горизонтальном следе плоскости.

 

 

Рис. 3.1.

 

Плоскость П₂ прямая АВ пересечет в точке N, расположенной на линии Р₂.

Иными словами, следы прямой, лежащей в плоскости, расположены на одноименных следах плоскости.

Отсюда следует, что следы плоскости должны проходить через одноименные следы прямых, лежащих в плоскости.

Чтобы построить след плоскости, необходимо определить следы двух прямых, лежащих в плоскости.

На рис. 3.1. плоскость задана двумя пересекающимися прямыми АВ и СD. Чтобы построить горизонтальный след плоскости необходимо найти горизонтальный след прямой АВ – точку М и прямой СD – точку М¹. Горизонтальный след плоскости будет проходить через точки М и М¹.

Фронтальный след плоскости Р₂ строится аналогично. Следует отметить, что для построения следа Р₂ достаточно иметь фронтальный след только одной прямой, так как второй точкой, определяющей положение следа Р₂ будет точка Р_х схода следов (точка пересечения ранее построенного следа Р₁ с осью х).