Проецирование прямой на три плоскости проекции.

 

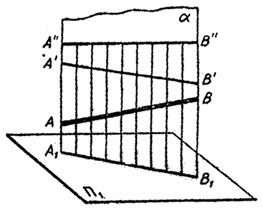
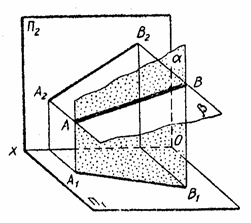
Прямую можно рассматривать как результат пересечения двух плоскостей (рис 2.1, 2.2.).

 

Рис. 2.1.

Рис 2.2.

 

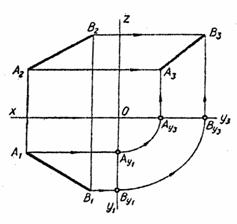
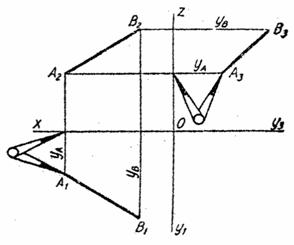
Прямая в пространстве безгранична. Ограниченная часть прямой называется отрезком.

Проецирование прямой сводится к построению проекций двух произвольных ее точек, так как две точки полностью определяют положение прямой в пространстве. Опустив из точки А и В (рис. 2.2.) перпендикуляры до пересечения с плоскостью П₁, определяют их ух горизонтальные проекции А₁ и В₁. Отрезок А₁В₁ – горизонтальная проекция прямой АВ. Аналогичный результат получают, проведя перпендикуляры к П₁ из произвольных точек прямой АВ. Совокупность этих перпендикуляров (проецирующих лучей) образует горизонтально проецирующую плоскость a, которая пересекается с плоскостью П₁ по прямой А₁В₁ – горизонтальной проекции прямой АВ. Исходя из тех же соображений, получают фронтальную проекцию А₂В₂ прямой АВ (рис 2.2).

Одна проекция прямой не определяет ее положение в пространстве. Действительно, отрезок А₁В₁ (рис. 2.1.) может быть проекцией произвольного отрезка, лежащего в проецирующей плоскости a. Положение прямой в пространстве однозначно определяется совокупностью двух ее проекций. Восставляя из точки горизонтальной А₁В₁ и фронтальной П₁ и П₂, получают две проецирующие плоскости a и b, пересекающиеся по единственной прямой АВ.

Рис. 2.3

На комплексном чертеже (рис 2.3) изображен отрезок АВ прямой общего положения, где А₁В₁ – горизонтальная, А₂В₂ – фронтальная и А₃В₃ – профильная проекции отрезка. Для построения третьей проекции отрезка. Для построения третьей проекции отрезка прямой по двум данным можно использовать те же способы, что и для построения третьей проекции точки: проекционный (рис 2.4.), координатный (рис 2.5.) и с использованием постоянной прямой чертежа (рис. 2.6.).

 

Рис. 2.4.

Рис. 2.5.

Рис. 2.6.

 

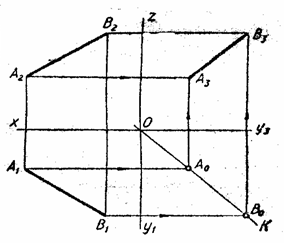
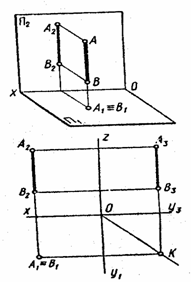
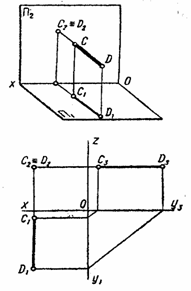
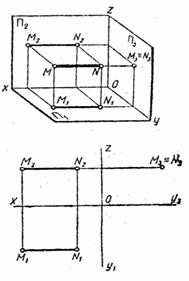
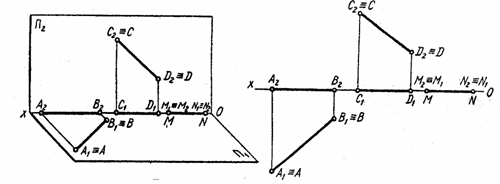
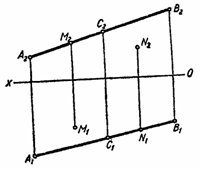
2.2. Положение прямой относительно плоскости проекций.

На рис 1.5. изображен параллелепипед со срезанной вершиной и произвольная треугольная пирамида. Ребра параллелепипеда и пирамиды занимают различные положения в пространстве относительно плоскостей проекций. Чтобы строить и читать чертежи, нужно уметь анализировать положения прямой. По своему положению в пространстве прямые распределяются на прямые частного и прямые общего положения.

Прямые частного положения могут быть проецирующими и прямыми уровня.

Проецирующими называются прямые, перпендикулярные к одной из плоскостей проекций, т.е. параллельные двум другим плоскостей П₁, называется горизонтально проецирующей прямой; ее горизонтальная проекция А₁В₁ – точка, а фронтальная и профильная проекции – прямые, параллельные оси О_z. Прямая CD (рис. 2.7.) перпендикулярная к плоскости проекций П₂, называется фронтально проецирующей прямой; ее фронтальная проекция С₂D₂ – точка, а горизонтальная и профильная проекции – прямые, параллельные оси Оу. Прямая MN (рис. 2.8.) перпендикулярная к плоскости проекций П₃, называется профильно проецирующей прямой; ее профильная проекция М₃N₃ – точка, а горизонтальная и фронтальная проекции – прямые, параллельные оси Ох.

 

Рис. 2.7.

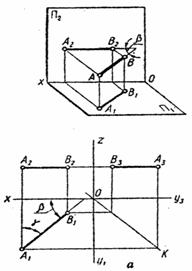
Рис. 2.8.

Следовательно, на одной из плоскостей проекций проецирующая прямая изображается в виде точки, а на двух других – в виде отрезков занимающих горизонтальное или вертикальное положение, величины которых горизонтальное или вертикальное положение, величина которых равна натуральной величине самого отрезка прямой.

Прямыми уровня называются прямые, параллельные одной из плоскостей проекций. Прямая АВ (рис. 2.9.), параллельная горизонтальной плоскости проекций П₁, называется горизонтальной прямой, или, сокращенно, горизонталью. Ее фронтальная проекция А₂В₂ параллельна оси проекций Ох, а горизонтальная А₁В₁ равна натуральной величине отрезка прямой (А₁В₁ = АВ). Угол b между горизонтальной проекцией А₁В₁ и осью Ох равен натуральной величине угла наклона прямой АВ к плоскости проекций П₂.

Рис. 2.9.

Прямая CD (рис. 2.10.) параллельная фронтальной плоскости проекций П₂, называется фронтальной прямой, или, сокращенно, фронталью. Ее горизонтальная проекция C₁D₁ параллельна оси Ох, а фронтальная С₂D₂ равна натуральной величине отрезка прямой (C₂D₂ = CD). Угол a между фронтальной проекцией С₂D₂ и осью Ох равен действительной величине угла наклона прямой к плоскости проекций П₁.

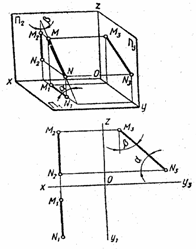
Рис. 2.10.

Прямая MN (рис. 2.11.) параллельная профильной плоскости проекций П₃, называется профильной прямой. Ее фронтальная M₂N₂ и горизонтальная M₁N₁ проекции перпендикулярны к оси Ох, а профильная проекция равна натуральной величине отрезка (M₃N₃ = MN). Углы a и b между профильной проекцией и осями Оу₃ и Оz равны действительной величине углов наклона прямой к плоскости проекций П₁ и П₂.

Рис. 2.11.

Следовательно, прямые уровня на одну из плоскостей проекций проецируются в натуральную величину, а на две другие – в вид отрезков уменьшенной величины, занимающих на чертеже вертикальное или горизонтальное положение. По чертежу можно определить величину углов наклона этих прямых к плоскостям проекций.

Если прямая лежит в плоскости проекций, то одна ее проекция (одноименная) совпадает с самой прямой, а две другие – с осями проекций. Например, прямая АВ (рис.2.12) лежит в плоскости П₁. Ее горизонтальная проекция А₁В₁ сливается с прямой АВ, а фронтальная А₂В₂ – с осью Ох. Подобную прямую называют нулевой горизонталью, так как высота ее точек (координата z) равна нулю.

Рис. 2.12.

Прямой общего положения называют прямую, наклонную ко всем плоскостям проекций. Ее проекции образуют с осями Ох, Оу и Оz острые или тупые углы, т.е. ни одна из ее проекций не параллельна и не перпендикулярна к осям. Величина проекций прямой общего положения всегда меньше натуральной величины самого отрезка. Непосредственно по чертежу без дополнительных построений нельзя определить действительную величину прямой и угла наклона ее к плоскостям проекций.

Если точка лежит на прямой, то проекции точки находятся на одноименных проекциях прямой и на общей линии связи.

На рис. 2.13. точка С лежит на прямой АВ, так как ее проекции С₁ и С₂ находятся соответственно на горизонтальной А₁В₁ и на фронтальной А₂В₂ проекциях прямой. Точки М и N не принадлежат прямой, так как одна из проекций каждой точки не находится на одноименной с ней проекции прямой.

Рис. 2.13.

Проекции точки делят проекции прямой в таком же отношении, в каком сама точка делит отрезок прямой, т.е. Пользуясь этим правилом, разделить данный отрезок прямой в нужном соотношении. Например, на рис. 2.14. прямая EF разделена точкой К в отношении 3:5. Деление выполнено способом, известным из геометрического черчения.

Рис.2.14.