Прямоугольная аксонометрия и ее свойства.

 

Для того чтобы направление проецирования было перпендикулярно картине, ее плоскость должно быть расположена под какими – то углами к пространственным осям координат. В этом случае треугольник следов в прямоугольной аксонометрии всегда остроугольный, аксонометрические оси являются высотами этого треугольника и образуют между собой тупые углы (рисунок 11.5)

Рисунок 11.5

 

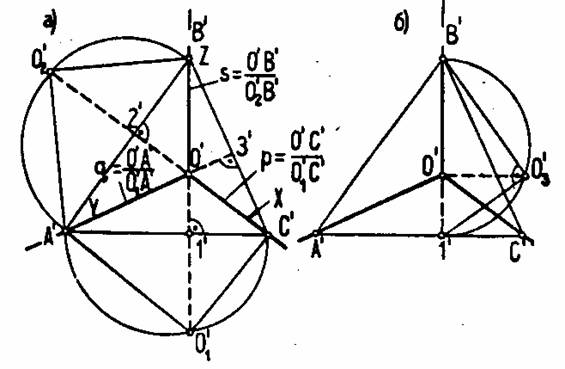
При решении ряда задач приходится определять натуральные размеры отдельных элементов изображенного объекта (длины отрезков, величины углов и пр.) или, наоборот, строить эти элементы по заданным условиям.

Метрические задачи в аксонометрии проще решать в том случае, если элемент тем или иным способом приведен в плоскость картины или в плоскость, параллельную ей. После операций, проделанных в плоскости картины, элемент надо привести в исходное положение. Наиболее распространенным и практически удобным способом является способ вращение до совпадения элемента с плоскостью картины или до положения, перпендикулярного к картине.

В первую очередь этот способ применяется для определения натуральных масштабов по произвольно выбраны аксонометрическим или, наоборот, для установления аксонометрических масштабов по натуральным точкам. Он так же используется для определения положения картины и направления проецирования по отношению к координатным плоскостям, если это требуется по ходу работы.

На рисунке 11.5 видно, что плоскость картины отсекает от координатных плоскостей треугольники, ограниченные двумя отрезками осей координат и стороной треугольника следов. Эти треугольники на картине проецируются искаженно, но сохраняют сторону треугольника следов.

Для нахождения натуральной величины этих треугольников, а следовательно, и отсеченных отрезков осей надо их совместить с плоскостью картине вращением вокруг следа картины; при этом точка О´ - проекция начала координат – будет перемещаться по перпендикуляру к стороне треугольника следов (следу плоскости Р) и расположится на дуге окружности, построенной на стороне треугольника следов, как на диаметре (рисунок 11.6 а).

Рисунок 11.6

 

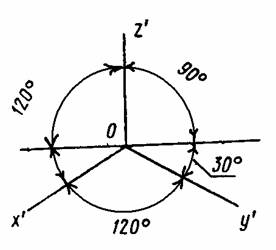
На совмещенных треугольниках будут определяться истинные величины отрезков координатных осей, а следовательно, и натуральные масштабы, что позволит установить показатели искажения, т.е. отношения аксонометрических масштабов к натуральным.

Но может быть выполнен и обратный процесс – определение положения осей аксонометрии по данным натуральным масштабам и выбранным показателям искажения.

Для определения натуральной величины отрезка только одной оси аксонометрии Z и натурального масштаба по ней вращение производится вокруг этой оси Z (рисунок 11.6 б), и совмещенное положение точки О´ будет так же на окружности, построенной на отрезке В´1´ как на диаметре. Здесь, как и в первом совмещении, будут установлены натуральный размер отрезка оси Z, натуральный масштаб и величина «сжатия» фигур, лежащих в горизонтальной плоскости, а следовательно, и «коэффициент сжатия» в направлении, параллельном оси Z, т.е. высоты объекта. Коэффициент сжатия – отношение О´1´: O´₃1´ в дальнейшем будет использована для решения позиционных и метрических задач, а так же для преобразования кривых 2-го порядка в более простые (окружности).

На изображения, выполняемые в аксонометрических проекциях, имеются ГОСТы (ГОСТ 2.317 – 69), которые рекомендую следующие виды аксонометрических изображений:

1. Два вида прямоугольных аксонометрических проекций (изометрию и диметрию).

2. Три вида косоугольных (фронтальную изометрию, горизонтальную изометрию, фронтальную диметрию).

Прямоугольная изометрия

В этом виде аксонометрии все углы между осями равны 120⁰, а все показатели искажения равно 0,82 (рисунок 11.7)

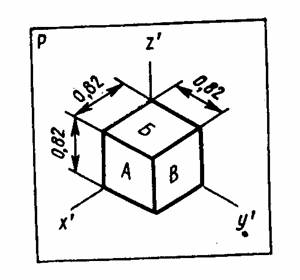
Рисунок 11.7

Это изображение обладает хорошей наглядностью, простое в построении, но объекты, приближающиеся к форме куба или имеющие квадратный план, в такой аксонометрии выполнять не рекомендуется, т.к. изображение иногда не создает достаточную наглядность. В это случае направление проецирования совпадает с одной диагональю куба, которая на изображении выражается в точку. (рисунок 11.7а)

Рисунок 11.7а

Для удобства построения вместо показателя 0,82 принимают приведенный показатель, равный 1, но при этом надо иметь в виду, что масштаб изображения будет больше масштаба ортогонального чертежа в 1/0,82 = 1,22 раза изображения очерка сферы на изображении будет окружностью радиусом 1,22 от радиуса в ортогональной проекции.

 

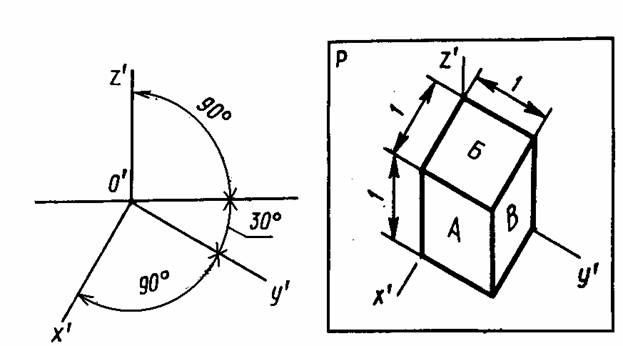
Прямоугольная диметрия.

В этом виде аксонометрии углы будут: между осями X и Z 90⁰+7⁰= 97⁰; между Z и Y 180⁰-48⁰ = 132⁰.

Показатели искажения: 0,94 по осям X и Z и 0,47 по оси Y. Обычно принимаются приведенные показатели соответственно 1 и 0,5. тогда размер изображенного объекта будет больше изображения на ортогональном чертеже с 1/0,94 = 1,06 раза, а следовательно, сфера изобразится окружностью радиусом 1,06 от радиуса ортогонального чертежа (рисунок 11.8)

Рисунок 11.8

 

Косоугольная аксонометрия.

Если плоскость картины расположить параллельно двум осям координат, допустим Z и X, то для получения их изображения, т.е. осей аксонометрии, направление проецирования уже нельзя принять перпендикулярно картине, т.к. в этом случае ось Y спроецируется в точку, а плоскость ZY выродится в прямую. Следовательно, направление проецирования надо принять под каким – то углом к картине, и только тогда получим изображение и третьей оси координат Y (рис.11.9, 11.9.а).

Рисунок 11.9 Рисунок 11.9а

В этом случае натуральные масштабы по осям Z и X и прямой угол между ними сохраняется, что значительно упрощает построение изображения. Направление проецирования может быть любым, но обычно ось Y располагают под углом 45⁰ или 30⁰ (к горизонту), а показатели искажения принимают 0,5 или 0,75. Этот вид изображения называется косоугольной диметрией. Он достаточно нагляден, прост в начертании и обычно выполняется так: вычерчивают фронтальную проекцию по ортогональному чертежу без изменения и по выбранному положению оси Y откладывают соответствующие размеры с учетом показателя искажения.

Если объект имеет очень сложную организацию в плане (т.е. в горизонтальной плоскости), то можно принять положение плоскости картины параллельно осям X и Y и так же косоугольно спроецировать начало координат. Получим косоугольную аксонометрию, в которой отсутствуют искажения по осям X, Y, а угол между ними останется равным 90⁰ (рис.11.10, 11.10.а, 11.11, 11.11а).

Рисунок 11.10 Рисунок 11.10а

 

Рисунок 11.11 Рисунок 11.11а

 

Ось Z обычно принимается вертикальной, и показатель искажения по ней так же берут равным 1. Этот наиболее простой по начертанию вид аксонометрии, но он уступает предыдущим по наглядности.