
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональные проекции прямойСодержание книги
Поиск на нашем сайте
Чтобы построить проекции какой-либо линии, нужно задать проекции двух ее точек и соответствующие проекции этих точек соединить (Рис.2.3). Относительно плоскостей проекций прямые могут занимать частные или общие положения.
Рис. 2.3. Проекции отрезка прямой Прямые частного положения К прямым частного положения относятся линии уровня – прямые, параллельные одной из плоскостей проекций, и проецирующие линии – прямые, перпендикулярные к одной из плоскостей проекций. У куба с вырезом (Рис.2.4) линии, расположенные в гранях куба, параллельны плоскостям проекций будут линиями уровня. Линия, параллельная горизонтальной плоскости проекций, называется горизонталью и на эпюре обозначается буквой h. Линия, параллельная фронтальной плоскости проекций, называется фронталью и обозначается буквой f. Линия, параллельная профильной плоскости проекций, называется профильной прямой и обозначается буквой р. Ребра куба, стоящего на плоскости Н так, как это показано на рис. 2.4, параллельны двум плоскостям проекций и перпендикулярны третьей. Их направление совпадает с направлением проецирующих прямых при прямоугольном проецировании. В зависимости от перпендикулярности к той или иной плоскости проекций, прямые называются:
Рис 2.4 Прямые частного положения
· линия, перпендикулярная горизонтальной плоскости проекций Н, называется – горизонтально проецирующей прямой (прямая d); · линия, перпендикулярная фронтальной плоскости проекций V, называется фронтально проецирующей прямой (прямая в); · линия, перпендикулярная профильной плоскости проекций W, называется профильно проецирующей прямой (прямая с). На рис.2.5 даны возможные положения прямых в системе плоскостей проекций в наглядном изображении и на эпюре. Фронтальная проекция горизонтали параллельна оси проекции Х, а на горизонтальной плоскости проекций она изображается в натуральную величину. На горизонтальной же проекции угол наклона горизонтали к фронтальной плоскости проекций изображается в натуральную величину. Аналогичны рассуждения относительно фронтали и профильной прямой. Угол между прямой и плоскостью определяется углом между прямой и ее проекцией на эту плоскость. Угол наклона прямой к горизонтальной плоскости проекций обозначается - a, к фронтальной - b, к профильной -
Рис 2.5 Проекция прямой частного положения
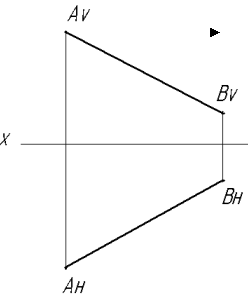
Прямая общего положения Прямая, непараллельная ни одной из плоскостей проекций, называется прямой общего положения (Рис.2.6а, б).
Рис. 2.6 Прямая общего положения: а)- в диметрии; б)- на эпюре По проекциям отрезка прямой общего положения можно представить себе положение этого отрезка в пространстве. Однако, ни одна из проекций отрезка прямой общего положения не дает его натуральной величины и углов наклона к плоскостям проекций.
2.2.3 Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций Натуральная величина отрезка прямой всегда может быть принята за гипотенузу прямоугольного треугольника, одним катетом которого является отрезок, равный и параллельный проекции, а другим – разность расстояний концов отрезка до плоскости проекций (Рис.2.7а, б).
Рис. 2.7. Определение натуральной величины отрезка и углов наклона: а) в диметрии; б) на эпюре В прямоугольном треугольнике АВВ В прямоугольном треугольнике АВА
Следы прямой линии Точки пересечения прямой линии с плоскостями проекций называют следами прямой линии (Рис.2.8а, б).
Рис. 2.8. Следы прямой: а) в диметрии; б) на эпюре
Продолжим прямую АВ до пересечения с плоскостью Н. Получим точку М, которая является горизонтальным следом прямой. Продолжая прямую АВ до пересечения с плоскостью V получим точку N – фронтальный след прямой. Чтобы на эпюре найти горизонтальный след, необходимо продолжить фронтальную проекцию AvBv до пересечения с осью Х; через точку пересечения Мv (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции прямой АнВн. Точка пересечения Мн является горизонтальной проекцией горизонтального следа (она совпадает с самим следом М). Для нахождения фронтального следа необходимо продолжить горизонтальную проекцию АнВн до пересечения с осью Х; через точку Nн (горизонтальную проекцию фронтального следа) провести перпендикуляр до пересечения с продолжением фронтальной проекции AvBv. Точка Nv является фронтальной проекцией фронтального следа (она совпадает с точкой N – самим фронтальным следом прямой).
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.005 с.) |


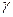 .
.


 - катет АВ
- катет АВ 



