Способ вспомогательных секущих плоскостей

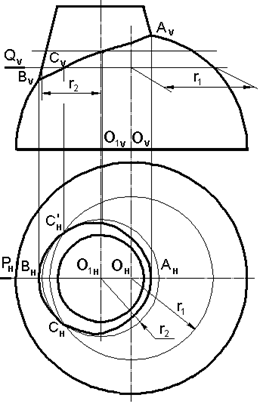
Сущность способа вспомогательных секущих плоскостей заключается в том, что для построения точек принадлежащих линии пересечения, вводится ряд вспомогательных секущих плоскостей, которые пересекали бы обе поверхности по графически простым линиям (окружностям и прямым). В пересечении контуров полученных сечений находят общие для двух поверхностей точки. Этот способ применяется как при взаимном пересечении кривых поверхностей, так и при пересечении кривых поверхностей с многогранниками.

Линия пересечения кривых поверхностей в общем случае будет пространственной кривой. При пересечении кривой поверхности с многогранником в каждой грани получается своя плоская кривая. Кривые, лежащие в смежных гранях, пересекаются на ребрах.

Задача: Построить линию пересечения конуса вращения с полусферой (рис.7.16).

Решение:

Для решения задачи могут быть использованы вспомогательные горизонтальные плоскости уровня, пересекающие обе поверхности по окружностям. С помощью таких плоскостей можно построить любое число произвольных точек.

Рис. 7.16. Пересечение конуса вращения с полусферой

Для того чтобы определить границы, в которых можно перемещать вспомогательные секущие плоскости и получать точки линии пересечения, необходимо определить верхнюю и нижнюю опорные точки. Плоскость Р – плоскость симметрии данных поверхностей (параллельная плоскости V) пересекает поверхности по их главным меридианам. Точки пересечения этих меридианов являются верхней А (А_v, А_н) и нижней В (В_v, В_н) точками линии пересечения.

Любая из горизонтальных плоскостей уровня, расположенных между этими точками, например, плоскость Q (Q_v) может быть использована для получения пары линии пересечения (точка С).

 

Способ вспомогательных сферических поверхностей

В основе способа вспомогательных сферических поверхностей лежит следующее положение: сфера с любой поверхностью вращения, ось которой проходит через центр сферы, пересекается по окружности. Если ось вращения параллельна плоскости проекций, то на эту плоскость такие окружности проецируются в прямые, перпендикулярные оси вращения (рис.7.17).

Рис. 7.17. Пересечение тел вращения со сферой

 

 

Способ вспомогательных сферических поверхностей применяется при определении линии пересечения тел вращения, оси которых пересекаются и параллельны одной и той же плоскости проекций.

Точку пересечения осей вращения принимают за центр концентрических сферических поверхностей и проводят ряд сфер, пересекающих обе поверхности.

В пересечении контуров получаемых окружностей находят общие для двух поверхностей точки. Наименьшей вспомогательной сферической будет поверхность, вписанная в большее тело.

Задача: Построить линию пересечения двух цилиндров, оси которых пересекаются и параллельны плоскости V (рис.7.18).

Решение:

· Находим опорные точки – точки пересечения крайних образующих цилиндра с наклонной осью с крайней правой образующей вертикального цилиндра. Это будут высшая и низшая точки линии пересечения (А_v и В_v).

· Для построения промежуточных точек проводится ряд концентрических сфер, центры которых, будут лежать в точке пересечения осей заданных цилиндров (О_v).

· Наименьшей сферической поверхностью здесь будет поверхность, вписанная в вертикальный цилиндр. Эта сфера касается вертикального цилиндра по окружности, которая проецируется в прямую 1v=2v, а наклонный цилиндр пересекает по окружности, проецирующуюся в прямую 3v=4v. Точка пересечения этих прямых (проекций окружностей) С_v и будет общей для обоих цилиндров.

Рис. 7.18. Линия пересечение двух цилиндров

 

 

· Для построения случайных (промежуточных) точек проведем ряд концентрических сфер. Рассмотрим построение этих точек на примере построения точки Д_v.

· Проводим сферу, радиус которой больше радиуса окружности основания вертикального цилиндра. Эта сфера пересекает цилиндры по окружностям, проецирующим в прямые 5_v - 6_v и 7_v-8_v. Точка пересечения этих прямых (Д_v) и будет точкой, принадлежащей линии пересечения двух цилиндров.

· Остальные точки строятся аналогично.