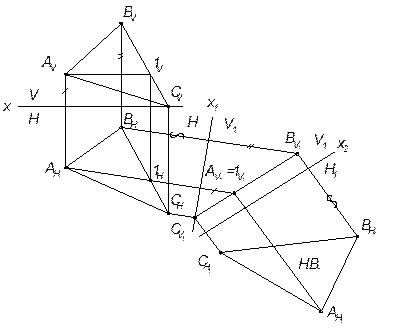Плоскости в плоскость уровня

 

 

Решение. Особенностью плоскостей уровня является то, что они проецируются на соответствующей плоскости проекций в натуральную величину. На рис.4.8 дана горизонтально проецирующая плоскость. Заменим плоскость проекций V на V₁ параллельную АВС и, следовательно, перпендикулярную к незаменимой плоскости Н. В системе V₁/H плоскость АВС будет плоскостью уровня, т.е. фронтальной плоскостью, поэтому дает натуральный вид этого треугольника.

Задача: Определить натуральную величину плоскости общего положения, заданную треугольником АВС (рис.4.9).

Решение. Для того, чтобы преобразовать плоскость АВС (рис.4.9) общего положения в плоскость уровня в новой системе плоскостей проекций, нужно последовательно решить две предыдущие задачи. Так как треугольник АВС задает плоскость общего положения, то для определения натуральной величины его следует преобразовать сначала в положение перпендикулярное к какой либо плоскости проекций (проецирующее), а затем, вторым преобразованием, привести в положение плоскости уровня, так как это показано на рис.4.9.

 

Способ вращения

Сущность этого способа заключается в том, что плоскости проекций остаются неизменными, а изменяется положение геометрического объекта в пространстве вращением вокруг некоторой оси. В качестве оси вращения выбирают или проецирующую прямую, или линию уровня.

Рис 4.9. Преобразование плоскости общего положения

В плоскость уровня

Вращение вокруг оси, перпендикулярной к плоскости

Проекций

Допустим, что точка А, расположенная в пространстве вращается вокруг оси i, перпендикулярной к фронтальной плоскости проекций V (рис.4.10а).

Проекцией вращающейся точки А на фронтальной плоскости проекций является окружность, а на горизонтальной прямая линия перпендикулярная оси вращения или параллельно оси Х (рис.4.11). Если ось вращения i перпендикулярна к плоскости Н, то горизонтальная проекция точки описывает окружность, а ее фронтальная проекция перемещается параллельно оси Х (рис.4.11).

Задача: Повернуть отрезок АВ до положения прямой уровня (рис.4.12).

Решение. Повернем отрезок, например, до положения фронтали. Для этого за ось вращения примем горизонтально-проецирующую прямую i, проходящую через точку В. При вращении точка В остается неподвижной, остается повернуть вокруг оси i точку А до положения, чтобы заданный отрезок стал параллельным фронтальной плоскости

Рис 4.10. Вращение точки вокруг оси в диметрии

Рис 4.11. Вращение точки вокруг оси на юпюре

 

проекций. Горизонтальная проекция траектории точки А есть дуга окружности, а фронтальная проекция есть прямая параллельная оси Х. Для поворота отрезка АВ до положения горизонтали нужно за ось вращения принять фронтально-проецирующую прямую, проведенную через какую-нибудь точку отрезка АВ.

При решении этих задач можно определить натуральную величину углов наклона отрезка к плоскостям проекций a и b. На рис. 4.10 показан, например, угол a.

 

Рис.4.10 Вращение прямой вокруг проецирующей оси

 

 

4.2.2. Вращение без указания осей на чертеже –