Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перпендикулярность прямых и плоскостей.Содержание книги Поиск на нашем сайте МЕТРИЧЕСКИЕ ЗАДАЧИ
4.1. Условие перпендикулярности двух прямых на комплексном чертеже 4.2. Условие перпендикулярности прямой к плоскости 4.3. Условие перпендикулярности плоскостей 4.4. Определение длины отрезка и углов наклона его к плоскостям проекций 4.5. Линия наибольшего наклона (ската)
4.1 Условие перпендикулярности двух прямых на комплексном чертеже Особый интерес с точки зрения решения задач начертательной геометрии представляют перпендикулярные прямые. Из классической Евклидовой геометрии известно следующее свойство перпендикулярности двух прямых: Две прямые перпендикулярны, если угол меду ними составляет 90°. Кроме того, в начертательной геометрии существует еще одно утверждение на эту тему: Две прямые перпендикулярны, если одна из них линия уровня. Для подтверждения этого заключения рассмотрим примеры, приведенные на рис. 4.1. Предположим что необходимо через точку А провести прямую ℓ, пересекающую горизонталь h прямым углом ℓ Так как одна из сторон h прямого угла параллельна плоскости π1, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию А1 проведем горизонтальную проекцию искомой прямой ℓ1 Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой ℓ
а) б) Рис. 4.1. Примеры построения перпендикулярных прямых: а) ℓ
4.2. Условие перпендикулярности прямой к плоскости Прямая а перпендикулярна плоскости α, если она перпендикулярна двум пересекающимся прямым b и с этой плоскости.
Если прямые b и с, принадлежащие плоскости α, расположены произвольно относительно плоскостей проекций, то прямые углы между прямой а и прямыми b и с спроецируются на плоскость проекций с искажениями. Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. е. являться соответственно горизонталью и фронталью плоскости α. Прямая а перпендикулярна плоскости α, если она перпендикулярна пересекающимся горизонтали h и фронтали f этой плоскости. При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений. Кроме вышесказанного существует теорема:
а) б)
Рис. 4.2. Изображение прямых, перпендикулярных к плоскостям заданным: а) плоскостью фигуры АВС; б) прямыми c, d
Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим проекциям горизонтали h и фронтали f этой плоскости. На рис. 4.2 изображены прямые перпендикулярные плоскостям, заданным различными способами. Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы. Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости (рис. 4.3).
Рис.4.3. Изображение прямой а перпендикулярной к плоскости, заданной следами
4.3. Условие перпендикулярности плоскостей
Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости. На рис. 4.3 показана прямая а перпендикулярная плоскости α, (следовательно, любая плоскость, проходящая через прямую а, будет перпендикулярна плоскости α. На рис. 4.4 изображены две проецирующие плоскости β и γ и произвольная плоскость δ, следы которой проходят через следы прямой а.
Рис. 4.4. Условие перпендикулярности плоскостей
Рис. 4.5. Условие перпендикулярности плоскостей
4.4. Определение действительной длины отрезка и углов наклона его к плоскостям проекций
Рис. 4.6. Определение углов наклона и натуральной величины отрезков
На рис. 4.6 показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А1В1. Проведя прямую ВВ’, параллельную горизонтальной проекции отрезка А1В1, получим прямоугольный треугольник Δ АВВ’. Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются горизонтальная проекция отрезка А1В1 и разность координат z точек А и В (Δz = zA- zB). Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и ее проекцией на плоскость (А1В1).
Рис. 4.7. Определение углов наклона и натуральной величины отрезков
Аналогично рассуждая (рис. 4.7), можно показать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY =YA- YB). Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°). По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА – ХВ) точек А и В. Угол γ° этого треугольника,
лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3. На рис. 4.8 показан пример определения длины отрезка АВ и углов наклона его к плоскостям проекций.
Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций
4.5. Линия наибольшего наклона (ската)
Главным свойством этой линии является то, что она образует с горизонтальной плоскостью проекций π1 угол α°, равный углу наклона плоскости γ к плоскости π1. Это свойство линии наибольшего наклона (ската) используется для определения углов наклона плоскостей к плоскостям проекций.
ЛЕКЦИЯ 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА 5. 1. Необходимость преобразований комплексного чертежа 5.2. Задачи на преобразование комплексного чертежа 5.3. Пути осуществления преобразования комплексного чертежа
5.1. Необходимость преобразований комплексного чертежа. Трудоемкость и, как следствие, точность графического решения задач часто зависят не только от сложности задач, но и от того, какое положение занимают геометрические фигуры, входящие в условие задачи, по отношению к плоскостям проекций. Проецируемая фигура может занимать по отношению к плоскостям проекций произвольное, или частное положение. В первом случае, как правило, получаются проекции, неудобные для решения задач. Решение задачи значительно упрощается, когда мы имеем дело с частным расположением геометрических фигур относительно плоскостей проекций. Наиболее выгодным частным положением проецируемой фигуры при ортогональном проецировании следует считать: 1) положение, перпендикулярное к плоскости проекций – при решении позиционных задач; 2) положение, параллельное плоскости проекций – для решения метрических задач. Таким образом, при решении той или иной задачи бывает целесообразно привести фигуру к частному положению. Переход от общего положения геометрической фигуры к частному можно осуществлять изменением взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями: 1) перемещением в пространстве проецируемой фигуры, по отношению к плоскости проекций. 2) выбором новой плоскости проекций, по отношению к проецируемой фигуре. Первый путь лежит в основе плоскопараллельного перемещения; второй – составляет теоретическую базу способа замены плоскостей проекций.
5.2. Задачи на преобразование комплексного чертежа Все метрические и позиционные задачи можно свести к одной из следующих четырех задач. Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня (горизонталь или фронталь) новой системы.
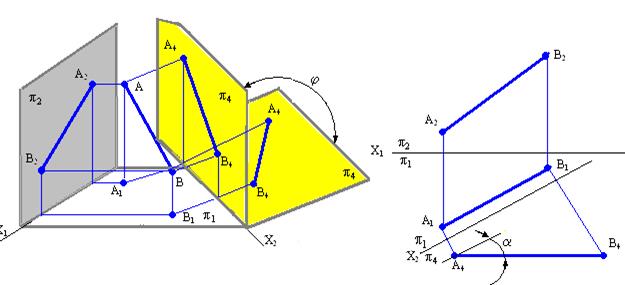 Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2 новой плоскостью П4 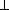 П1 и параллельной прямой АВ. П1 и параллельной прямой АВ. Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.1), необходимые для решения первой основной задачи на преобразование комплексного чертежа: 1) провести новую ось проекций х14 параллельно А1В1 на произвольном расстоянии от нее; такое положение оси х14 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х14 = А1В1; 2) выбрать на прямой две точки А(А1А2) и В(В1В2); 3) построить проекции точек А и В на плоскости П4; 4) Рис. 5.1. Преобразование прямой общего положения в прямую уровня
прямая А4В4 является проекцией прямой АВ на плоскость П4. Прямая AB в новой системе плоскостей проекций П1/П4 является фронталью, Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. | А4В4 | = | АB |, a- величина угла наклона прямой АВ к плоскости П1.
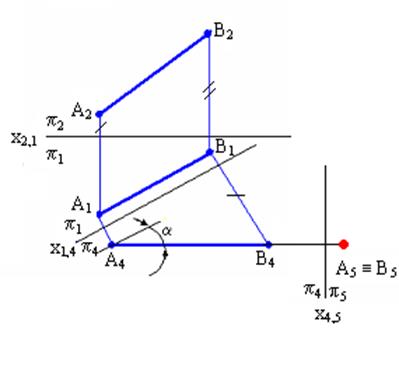 3адача 2. Преобразовать линию общего положения АВ в проецирующую прямую. Решение. 3адача 2. Преобразовать линию общего положения АВ в проецирующую прямую. Решение.
так как АВ // П4 и образует с ней новую систему плоскостей проекций П1/П4. Построения на комплексном чертеже: 1) проводим новую ось проекций х14 // А1В1; 2) построим проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2. 3) Заменим плоскость П1 на новую П5, которая будет 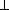 П4 и А4В4. Для этого проводим новую ось проекций х4,5. Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5. Прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и является горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из старых плоскостей проекций, и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций. П4 и А4В4. Для этого проводим новую ось проекций х4,5. Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5. Прямая АВ (А5В5) в новой системе плоскостей проекций заняла проецирующее положение и является горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из старых плоскостей проекций, и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.
Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Вначале прямую следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую. На рис.5.2 показано преобразование прямой АВ общего положения в горизонтально проецирующую.
Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения в новой системе плоскостей проекций стала проецирующей (рис. 5.3).
 (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости  , преобразовать в проецирующую, то плоскость , преобразовать в проецирующую, то плоскость  в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня. в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня.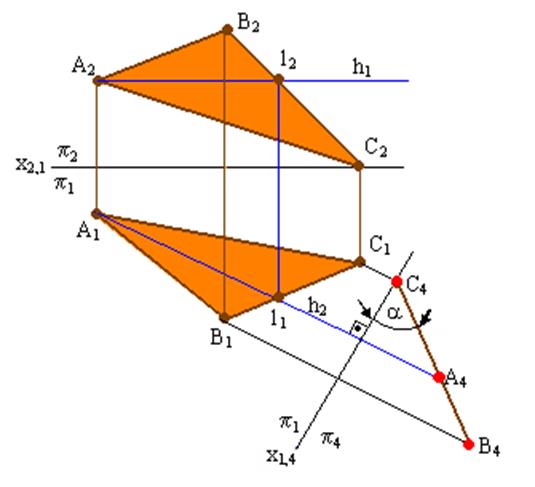
Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций. Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3, а затем проецирующую плоскость преобразовать в плоскость уровня. На рис. 5.4 показано преобразование плоскости ∆(АВС) в горизонтальную плоскость уровня. Допустим, что заданная плоскость Г является фронтально проецирующей (рис. 5.5). Заменим плоскость П1 новой плоскостью проекций П4, параллельной
1) проводим новую ось проекций х24 параллельно А2С2 на произвольном от нее расстоянии; такое положение оси проекций х24 обусловливается тем, что П4 параллельна Г (АВС). Ось х24 совпадает с прямой (А2С2), если плоскость П4 совмещается с плоскостью Г (АВС); 2) построим проекции точек А, В и С на плоскость П4;
Примечание. Так как плоскость треугольника АВС параллельна П4, значит отображение этого треугольника на П4 будет в натуральную величину. В данном курсе лекций рассматривается только способ замены плоскостей проекций. ЛЕКЦИЯ 6 МЕТРИЧЕСКИЕ ЗАДАЧИ 6.1. Общие положения 6.2. Задачи на определение расстояний между геометрическими фигурами
Метрическими (от греческих слов metron (греч.) – мера, metreo –мерю) называют задачи, решение которых связано с измерением расстояний и углов и других метрических характеристик. В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям. Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. аксиомы параллельного проецирования). Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических фигур, называют комплексными. 6.2. ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ Искомое расстояние во всех задачах этой группы измеряется длиной отрезка, заключенного между заданными геометрическими фигурами и перпендикулярного к одной из них (задачи 1 и 4) или одновременно к обеим (задачи 2, 3 и 5). Этот отрезок проецируется в конгруэнтный ему отрезок на плоскость проекций, которая будет перпендикулярна одной (задачи 1, 3 и 4) или обеим (задачи 2 и 5) геометрическим фигурам, между которыми определяется расстояние. Алгоритм решения задач этой группы будет следующим:
Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую АВ. Отрезок [МN] спроецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой АВ. Составляем алгоритм решения: 1. Преобразовать прямую АВ в проецирующую прямую способом замены плоскостей проекций. 2. Построить проекцию отрезка [МN] на плоскость П5  АВ, длина которого М5N5 определяет искомое расстояние. АВ, длина которого М5N5 определяет искомое расстояние.Построение. Для преобразования прямой АВ общего положения в проецирующую выполнены две последовательные замены плоскостей проекций: вначале прямая АВ преобразована в линию уровня, затем ли- ния уровня преобразована в проецирую- щую прямую. Построены проекций М4 и М5 точки М в системе П4/П5.
Отрезок [М5N5] является искомым: [М5N5] Задача 2. Определить расстояние между параллельными прямыми а и b. Для решения задачи необходимо выполнить две замены плоскостей проекций. Вначале прямые a и b необходимо сделать прямыми уровня. Для этого П4 необходимо расположить параллельно a1 и b1. Затем названные прямые необходимо расположить перпендикулярно П5. Расстояние между а5 и b5 будет натуральной величиной между параллельными прямыми a и b (рис. 6.2).
параллельно П4, потому что в плоскости П4 имеется ее натуральная величина. 2) Задачи 1- 5 можно также решать по следующей схеме: вначале определить метрически искаженные проекции искомого отрезка, а затем способом прямоугольного треугольника определить его действительную величину. Для решения задачи необходимо одну из заданных прямых преобразовать двойной заменой плоскостей проекций в проецирующую. Из точки этой прямой опустить перпендикуляр на вторую прямую. Этот перпендикуляр и будет расстоянием между заданными прямыми. Задача 4. Определение расстояния от точки до плоскости. Решение задачи приведено на рис. 6.3.
Для определения расстояния от точки М до плоскости треугольника ∆АВС необходимо плоскость треугольника общего положения ∆АВС преобразовать в плоскость проецирующую. Для этого нужно произвести замену плоскости проекций П2 на П4 перпендикулярно h1. Плоскость ∆АВС преобразуется в линию С4А4В4. На эту же плоскость П4 спроецируется точка М (М4). Перпендикуляр из М4 на линию С4А4В4 будет натуральной величиной расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи. расстояния от точки М до плоскости ∆АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи. Примечания: 1) Проекция перпендикуляра М1N1 в П1 располагается параллельно П4, потому что в плоскости П4 имеется ее натуральная величина. 2) Задачи 1- 5 можно также решать по следующей схеме: вначале определить метрически искаженные проекции искомого отрезка, а затем способом прямоугольного треугольника определить его действительную величину.
6.3. ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ВЕЛИЧИН
Общей схемой решения задач этой группы является приведение заданной плоской фигуры или плоскости угла в положение, параллельное одной из плоскостей проекций.
Углом между прямой и плоскостью называется угол между этой прямой и ее прямоугольной проекцией на данную плоскость. Решение задачи приведено на рис. 6.4. Для определения угла между прямой АВ и плоскостью S (а || b) необходимо: 1) Определить направление горизонтальной проекции горизонтали h1 и фронтальной проекции фронтали плоскости å (а || b).
3) Определить величину угла y вращением его вокруг горизонтали до положения, параллельного плоскости П1. 4) Вычислить значение искомого угла j = 90° – y°
Мерой угла между двумя плоскостями служит линейный угол, образованный двумя прямыми – сечениями граней этого угла плоскостью, перпендикулярной к их ребру. Пример определения угла между двумя плоскостями S (∆АВС) и G (∆АВD) приведен на рис. 6.5. В задаче необходимо линию пересечения АВ плоскостей S и G преобразовать в прямую уровня, а затем в линию проецирующую
6.4. ЗАДАЧИ НА ПОСТРОЕНИЕ В ПЛОСКОСТИ ОБЩЕГО РАЗМЕРАМ
Общей схемой решения задач этой группы является:
Лекция 7 ПОВЕРХНОСТИ 7.1. Понятия и определения 7.2. Линейчатые поверхности 7.1. Понятия и определения В начертательной геометрии фигуры задаются графически, поэтому целесообразно рассматривать поверхность как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующейся на таких основных элементарных геометрических понятиях, как точка и множество. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности: Поверхностью называется непрерывное двупараметрическое множество точек. Для получения наглядного изображения поверхности на чертеже закон перемещения линии целесообразно задавать графически в виде совокупности линий и указаний о характере перемещения линии. Эти указания могут быть заданы графически, в частности с помощью направляющей поверхности. В процессе образования поверхностей линия может оставаться неизменной или менять свою форму. Такой способ образования поверхности называется кинематическим, а сама поверхность- кинематической. Примером такого способа образования могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» профиля резца. Режущие кромки являются неотъемлемой частью исполнительных механизмов многих строительных и дорожных машин, применяемых не только для разработки и перемещения грунта (бульдозеры, грейдеры и т. п.), но и рытье траншей, котлованов, проходка траншей, профилирование откосов и многое другое. Но режущие кромки во многих случаях начинают уступать место производящей поверхности, с которой связано развитие прогрессивных производительных процессов обработки металлов давлением и обкаткой. Геометрическая сущность этих процессов – метод огибания.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1938; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.014 с.) |

 h (рис. 4.1.а).
h (рис. 4.1.а).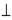 h1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали N1= ℓ1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения N2. Точки А2 и N2 определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.
h1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали N1= ℓ1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения N2. Точки А2 и N2 определяют фронтальную проекцию искомой прямой ℓ. Две проекции прямой определяют ее положение в пространстве.
 Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция − к фронтальной проекции фронтали этой плоскости.
Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция − к фронтальной проекции фронтали этой плоскости.

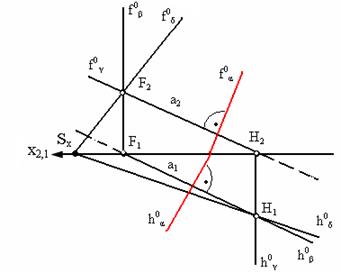
 На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.
На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.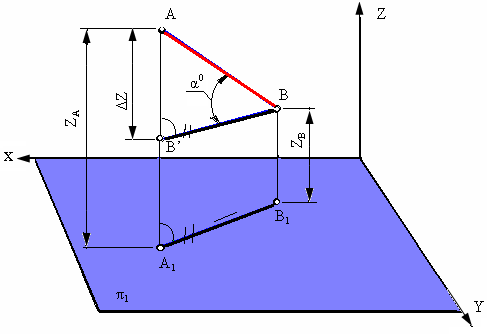
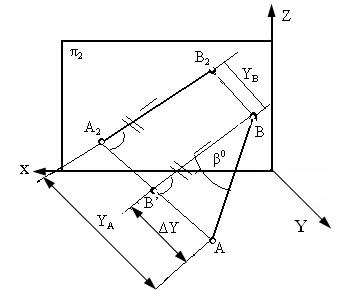 Следовательно, угол Δ АВВ’, лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π1 (угол α°).
Следовательно, угол Δ АВВ’, лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π1 (угол α°).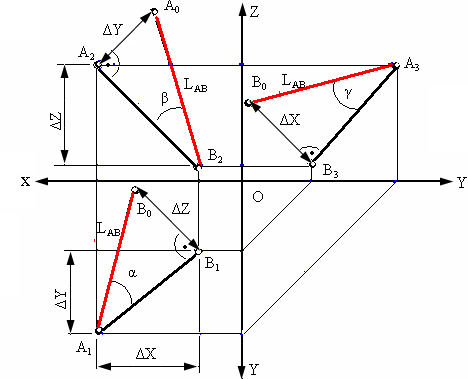
 Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис.4.9). На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали.
Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис.4.9). На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали.
 На чертеже плоскость
На чертеже плоскость  - величина угла наклона плоскости
- величина угла наклона плоскости 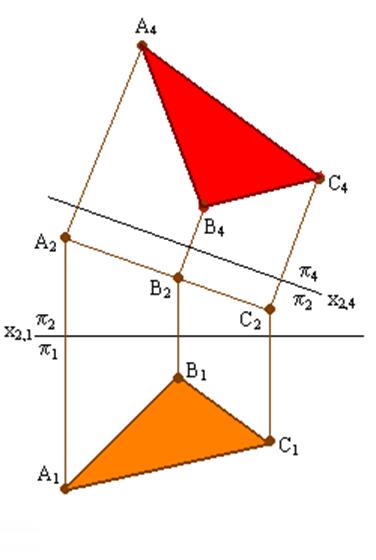 плоскости Г (∆АВС) и, перпендикулярной незаменяемой плоскости П2. В новой системе плоскостей проекций П2/П4 плоскость Г (АВС) станет горизонтальной плоскостью уровня.
плоскости Г (∆АВС) и, перпендикулярной незаменяемой плоскости П2. В новой системе плоскостей проекций П2/П4 плоскость Г (АВС) станет горизонтальной плоскостью уровня.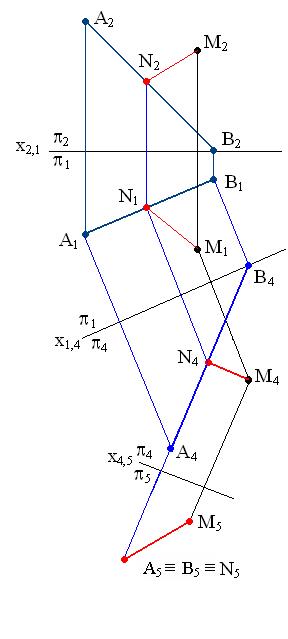
 [МN] и /М5N5/ = /МN/.
[МN] и /М5N5/ = /МN/.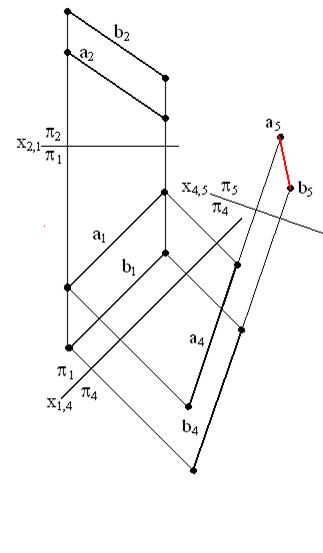
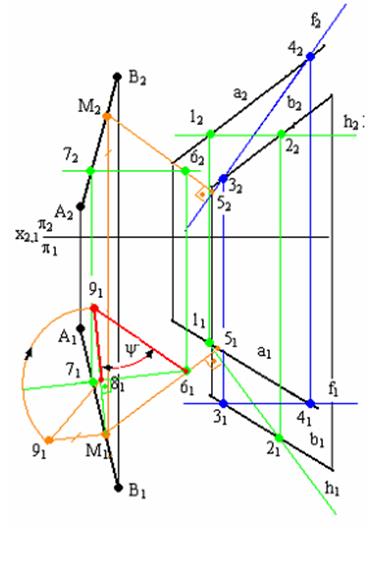 Задача 3. Определение вели- чины угла, образованного прямой и плоскостью.
Задача 3. Определение вели- чины угла, образованного прямой и плоскостью.