Точка, прямая и плоскость на комплексном чертеже

 

 

2.1. Ортогональные проекции точки и прямой.

2.2. Частные случаи расположения прямой в пространстве

2.3. Следы прямой линии

2.4. Ортогональная проекция плоскости

2.5. Частные случаи расположения плоскостей в пространстве

2.6. Следы плоскости

 

 

2.1. Ортогональные проекции точки и прямой.

 

Точка, как математическое понятие не имеет размеров. Очевидно. Если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.

В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку будем принимать шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.

При построении прямых необходимо знать следующие свойства прямой на комплексном чертеже (эпюре):

1. Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая прямая может быть задана проекциями двух ее точек. Прямую на комплексном чертеже можно задать и ее проекциями.

 

2. Всякая непрофильная прямая вполне определяется двумя своими проекциями, для определения же профильной прямой необходимо задать на проекциях прямой проекции ее двух точек

 

3. Чтобы задать на одной профильной прямой какую-нибудь точку, достаточно задать ее проекции на одноименных проекциях данной прямой.

 

4. Для деления данного отрезка в данном отношении достаточно разделить в этом отношении одну из проекций данного отрезка, а затем спроецировать делящую точку на другую проекцию отрезка.

 

 

2.2. Частные случаи расположения прямой в пространстве

 

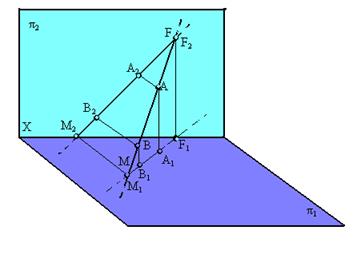
На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.

 

 

 

 

Рис. 2.1. Изображение прямых общего положения

 

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.

 

Прямые, параллельные плоскостям проекций.

 

1. Горизонтальная прямая h (рис. 2.2) – горизонталь

Рис. 2.2. Изображение горизонтальной прямой

 

Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций p₁.

Так как все эти точки этой прямой равноудалены от плоскости проекций p₁ (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций p₁ проецируются без искажения отрезок прямой АВ (А₁В₁=АВ) и углы наклона прямой к плоскостям проекций p₂ и p₃ (углы b° и g°).

 

 

2. Фронтальная прямая f (рис. 2.3) – фронталь

Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций p₂. Т. к. все точки этой прямой равноудалены от плоскости проекций p₂ (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций p₂ проецируются без

 

искажений отрезок этой прямой CD (C₂D₂+CD) и углы наклона прямой к плоскостям проекций p₁ и p₃ (углы a° и g°)

 

 

Рис. 2.3. Изображение фронтальной прямой

 

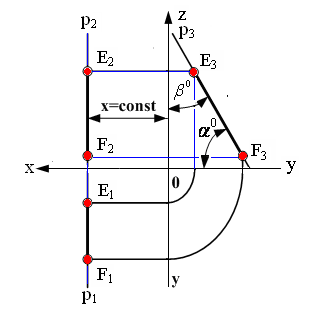
3. Профильная прямая p (рис. 2.4)

 

Профильная прямая – это прямая, параллельная профильной плоскости проекций p₃ . Так как все точки этой прямой равноудалены от плоскости проекций p₃ (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций p₃

 

 

проецируется без искажения отрезок этой прямой EF (E₃F₃=EF)и углы наклона прямой к плоскостям проекций p₁ и p₂ (углы a° и b°)

 

 

 

Рис. 2.4. Изображение профильной прямой

 

Прямые, принадлежащие плоскостям проекций

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

 

 

Рис. 2.5. Изображение прямой, принадлежащей горизонтальной плоскости проекций

 

 

 

Рис. 2.6. Изображение прямой, принадлежащей фронтальной плоскости проекций

 

На рис. 2.5,2.6,2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).

 

 

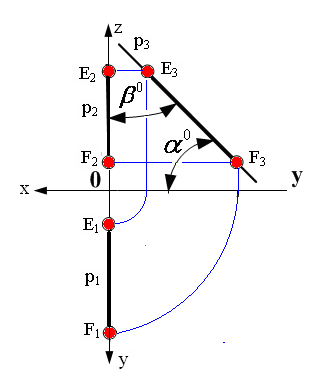
Рис. 2.7. Изображение прямой, принадлежащей профильной плоскости проекций

Прямые, перпендикулярные плоскостям проекций

Проецирующие прямые

 

 

На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций

 

Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость p₁ в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).

 

Рис. 2.8. Изображение прямой, перпендикулярной горизонтальной плоскости проекций

 

Прямая перендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость p₂ в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9)

 

 

Рис. 2.9. Изображение прямой, перпендикулярной фронтальной плоскости проекций

 

Прямая перендикулярная профильной плоскости проекций – профильнольно-проецирующая прямая. Эта прямая проецируется на плоскость p₃ в точку, а ее фронтальная проекция перпендикулярна оси Z

 

Рис. 2.10. Изображение прямой, перпендикулярной профильной плоскости проекций

 

 

Эти прямые являются частными случаями фронтали и горизонтали.

 

Следы прямой линии

Следом прямой линии называется точка пересечения прямой с плоскостью проекций.

В системе двух плоскостей проекций p₁ и p₂ прямая в общем случае имеет два следа (рис. 2.11 а,б):

1. Горизонтальный Н (Н₁, Н₂);

2. Фронтальный F (F₁, F₂)

 

 

 

а) б)

 

Рис. 2.11. Изображение следов прямой линии: а) в пространстве; б) на эпюре

Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций.

Установим правило нахождения следов прямой.

 

Для нахождения горизонтального следа прямой необходимо:

1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку Н_Х º Н₂)

2) восстановить перпендикуляр в точке Н_Х к оси Х (провести линию связи перпендикулярную к оси Х);

3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;

4) полученная точка пересечения и будет являться горизонтальным следом прямой а Н º Н₁

 

Для нахождения фронтального следа прямой необходимо:

1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка F_Xº F₁);

2) восстановить перпендикуляр в точке F_X к оси Х;

3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;

4) полученная точка пересечения Fº F₂ является фронтальным следом прямой а

 

В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическим фигурами будут только те, которые расположены в первом октанте.

Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.

 

2.4.Ортогональная проекция плоскости

 

На эпюре плоскость может быть задана графически одним из следующих способов, показанных на рис. 2.12.

 

 

а) б)

 

	в)
		г)

в)

 

 

 

 

 

 

д) е)

 

 

ж)

 

Рис. 2.12. Способы задания плоскости: а − тремя точками не лежащими на одной прямой; б − прямой и точкой вне ее; в − двумя пересекающимися прямыми; г − двумя параллельными прямыми; д, е − плоской фигурой; ж − следами плоскости

 

2.5. Частные случаи расположения плоскостей в пространстве

 

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекции.

 

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости.

 

1. Горизонтально проецирующая плоскость a^p₁.

 

 

Рис. 2.13. Изображение горизонтально-проецирующей плоскости

 

Плоскость a, перпендикулярная горизонтальной плоскости проекции p₁, называется горизонтально проецирующей (рис. 2.13).

Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на p₁ в прямую линию (горизонтальный след плоскости h_0a).

Угол b, который составляет горизонтальный след плоскости h_0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p₂. Фронтальный след такой плоскости перпендикулярен оси Х (f_0a ^ X).

 

2. Фронтально проецирующая плоскость b ^ p₂. Плоскость b перпендикулярная фронтальной плоскости проекций p₂ называется фронтально проецирующей (рис. 2.14).

 

 

 

Рис. 2.14. Изображение фронтально-проецирующей плоскости

 

Основным свойством фронтально-проецирующей плоскости является то, что любая фигура. Расположенная в этой плоскости, проецируется на p₂ в прямую линию (фронтальный след плоскости f_0b). Угол a, который составляет фронтальный след плоскости f_0b с координатной осью Х, равен углу наклона плоскости b к плоскости проекций p₁. Горизонтальный след такой плоскости перпендикулярен оси Х.

 

Плоскости, параллельные плоскостям проекций

(плоскости уровня)

 

 

1. Горизонтальная плоскость g÷÷p₁.

 

Плоскость g, параллельная плоскости p₁, называется горизонтальной (рис. 2.15).

 

 

Рис. 2.15. Изображение плоскости, параллельной горизонтальной плоскости проекций

 

Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскости проекций в натуральную величину (D А₁В₁С₁=DАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f_0g½½Х).

 

2. Фронтальная плоскость d½½p₂.

 

Плоскость d, параллельная плоскости p₂, называется фронтальной.

Любая фигура расположенная в такой плоскости. Проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.

Плоскость общего положения

 

Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.16.а).

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.

 

2.6. Следы плоскости

 

Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций.

а б

 

Рис. 2.16. Пример изображения следов плоскости: а) в пространстве;

б) на комплексном чертеже

 

В системе двух плоскостей проекций p₁ и p₂ плоскость в общем случае имеет два следа: горизонтальный h_a⁰ и фронтальный f_a⁰, которые являются пересечением плоскости a соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.16).

Точки пересечения плоскости a с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно S_x, S_y, S_z (рис. 2.16.а).

Главные линии плоскости

Главными линиями плоскости называют:

1. Горизонталь − прямую, принадлежащую плоскости и параллельную горизонтальной плоскости проекций.

2. Фронталь − прямую, принадлежащую плоскости и параллельную фронтальной плоскости проекций.

3. Линию наибольшего наклона − прямую, принадлежащую плоскости и перпендикулярную к горизонтали или фронтали этой плоскости.

 

 

Лекция 3