
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение двух плоскостей, когда одна из них частного положенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Результатом пересечения двух плоскостей является прямая, поэтому для ее определения достаточно найти две точки, принадлежащие одновременно каждой из двух заданных плоскостей. На рис. 5.2 заданы плоскости ABC и DEF. ABC – плоскость общего положения, DEF – горизонтально-проецирующая. Построим линию их пересечения MN.
Определим видимость линий на фронтальной плоскости проекций. При взгляде на горизонтальные проекции плоскостей снизу очевидно, что A′′C′′M′′N′′ находится перед D′′E′′F′′, что подтверждает анализ видимости конкурирующих точек 1 и 2. Невидимые участки линий изображены штриховой линией.
Пересечение прямой общего положения С плоскостью общего положения На рис. 5.3 даны плоскость общего положения ABC и прямая общего положения l. В этом случае для построения точки пересечения пользуются следующим алгоритмом.
2) Находят линию пересечения заданной и вспомогательной плоскостей. ABC 3) Точка пересечения найденной линии и заданной является искомой. 1-2 Видимость линий определяется аналогично при помощи конкурирующих точек: на горизонтальной плоскости проекций – 2 и 3, на фронтальной плоскости проекций – 4 и 5.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Условия параллельности и перпендикулярности прямых и плоскостей 2. Как построить точку пересечения прямой и плоскости частного положения? 3. Как построить линию пересечения двух плоскостей, если одна из них частного положения? 4. Как построить точку пересечения прямой общего положения и плоскости общего положения? 5. Как определить видимость линий при взаимном пересечении плоскостей?
- 1 - 2 - 3 7. Какой участок прямой l на фронтальной плоскости проекций является невидимым?
- 1 - 2 - 2 - 3
8. Линией пересечения плоскостей ABC и заданной пересекающимися прямыми а и в, является …
- 1 - 2 - 3 - 4
9. Какой участок плоскости ABC на горизонтальной плоскости проекций является невидимым?
- А12 - 12ВС - А34 - 34ВС
ЗАНЯТИЕ 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА Метрические задачи - это задачи, связанные с определением различных величин геометрических фигур (натуральных величин отрезка и плоскости, величины углов, кратчайших расстояний и т.д.). В начертательной геометриизадачи решаются графически. Количество геометрических построений и их характер при этом определяется не только сложностью задачи, но и в значительной степени зависят от того, с какими проекциями приходиться иметь дело (удобными или неудобными). Задачи решаются значительно проще в случае частного положения геометрической фигуры относительно плоскости проекций. Переход от общего положения к частному осуществляют, используя способыпреобразования чертежа. Четыре основные задачи преобразования: 1. Преобразовать чертеж так, чтобы прямая общего положения заняла положение прямой уровня. 2. Преобразовать чертеж так, чтобы прямая общего положения заняла положение проецирующей прямой. 3. Преобразовать чертеж так, чтобы плоскость общего положения заняла положение проецирующей плоскости. 4. Преобразовать чертеж так, чтобы плоскость общего положения заняла положение плоскости уровня.
|
||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.006 с.) |

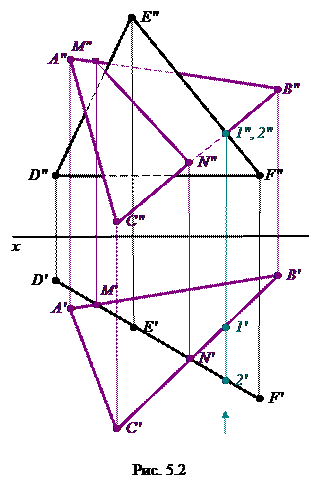 Поскольку, DEF проецируется в прямую линию на горизонтальную плоскость проекций, то M′N′ совпадает с D′E′F′. A′B′
Поскольку, DEF проецируется в прямую линию на горизонтальную плоскость проекций, то M′N′ совпадает с D′E′F′. A′B′  D′E′F′ = M′, B′C′
D′E′F′ = M′, B′C′  A′′B′′, N′′
A′′B′′, N′′ 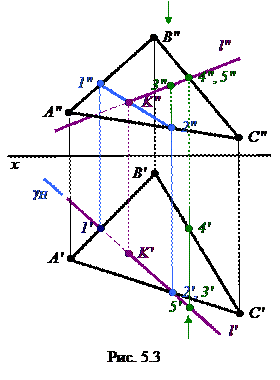 1) Заданную прямую заключают в вспомогательную проецирующую плоскость. На рис. 5.3 прямая l заключена в горизонтально-проецирующую плоскость γ, γН – горизонтальный след плоскости.
1) Заданную прямую заключают в вспомогательную проецирующую плоскость. На рис. 5.3 прямая l заключена в горизонтально-проецирующую плоскость γ, γН – горизонтальный след плоскости. γ = 1-2.
γ = 1-2. 6. Точкой пересечения прямой l и плоскости, заданной параллельными прямыми а и в является …
6. Точкой пересечения прямой l и плоскости, заданной параллельными прямыми а и в является …





