
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые, принадлежащие плоскости проекцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямые, принадлежащие плоскости проекций, являются частным случаем прямых уровня. Характерным признаком таких прямых будет принадлежность двух проекций прямой координатным осям. На рис. 3.9 прямая а принадлежит плоскости П1, на рис. 3.10 – плоскости П2,на рис. 3.11 - плоскости П3.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Если прямые в пространстве параллельны, то на чертеже параллельны их одноименные проекции. На рис. 3.12 – m ║ n.
Если прямые в пространстве пересекаются, то на чертеже пересекаются их одноименные проекции. При этом проекции точек пересечения лежат на одной линии связи. На рис. 3.13 – m ∩ n = K.
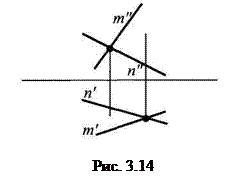
Если прямые в пространстве скрещиваются, то на чертеже их одноименные проекции могут пересекаться, но проекции точек пересечения не лежат на одной линии связи. На рис. 3.14 – m ÷ n.
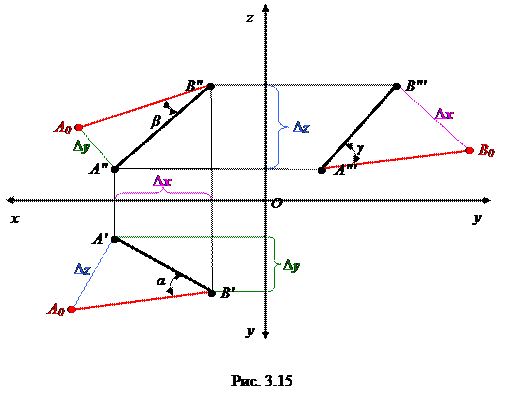
ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА МЕТОДОМ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА Метод применяется для определения натуральной величины отрезка общего положения. Натуральная величина отрезка общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция на одну из плоскостей проекций, а другим - разность расстояний концов отрезка от этой же плоскости. На рис. 13.15 натуральная величина отрезка АВ равна А0В′ = А0В′′ = А″′В0. Угол между катетом - проекцией и гипотенузой прямоугольного треугольника равен истинной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения. Таким образом: α - угол наклона отрезка АВ к горизонтальной плоскости проекций; β - угол наклона отрезка АВ к фронтальной плоскости проекций; γ - угол наклона отрезка АВ к профильной плоскости проекций.
ТЕОРЕМА О ПРЯМОМ УГЛЕ Для ортогонального проецирования справедлива теорема: для того чтобы прямой угол проецировался без искажений необходимо и достаточно, чтобы одна из его сторон была параллельна плоскости проекций, а вторая – не перпендикулярна к этой плоскости (рис. 3.16).
∟ ABC = 90º, AB ║ П1, BC не перпендикулярна П1, следовательно, ∟ A′B′C′ = 90º.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Как определить положение прямой относительно плоскостей проекций? 2. Как располагается горизонтальная проекция отрезка, если его фронтальная проекция равна самому отрезку? 3. Как называется прямая, если две ее проекции параллельны двум плоскостям проекций? 4. Как определить по проекциям прямых их взаимное положение? 5. Каким способом можно определить натуральную величину отрезка общего положения? 6. На каком чертеже прямая l является горизонтально-проецирующей?
- рис. б) - рис. в)
- рис. а) - рис. б) - рис. в)
8. На каком чертеже прямые c и d является параллельными?
- рис. а) - рис. б) - рис. в)
- рис. а) - рис. б)
10. Прямой а принадлежат точки …
- А и Е - В и D - В и Е - D и Е
ЗАНЯТИЕ 3
|
|||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.105 (0.006 с.) |




 На рис. 3.16 изображено:
На рис. 3.16 изображено: - рис. а)
- рис. а) 7. На каком чертеже прямая а является прямой общего положения,?
7. На каком чертеже прямая а является прямой общего положения,? 9. На каком чертеже прямые m и n является пересекающимися, скрещивающимися?
9. На каком чертеже прямые m и n является пересекающимися, скрещивающимися? - рис. в)
- рис. в)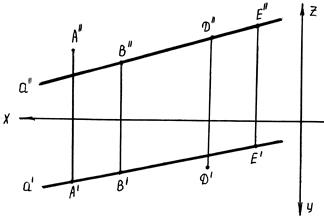 - А и D
- А и D


