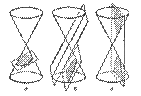Точка и прямая в плоскости. Главные линии плоскости (горизонталь, фронталь).

Точка и прямая в плоскости. Главные линии плоскости (горизонталь, фронталь).

Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (ΔКLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α ((ΔКLM), то пряма АВ, проходящая через эти точки, принадлежит плоскости α.

Горизонталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ, параллельную оси х.

Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости.

Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекцияф параллельна оси х.

Построение линий пересечения поверхностей.

Линия пересечения поверхностей состоит из точек, принадлежащих каждой из них. Общий способ построения линии пересечения заключается в последовательном нахождении точек, ей принадлежащих, при помощи вспомогательных секущих поверхностей - посредников. В качестве посредника выбирается плоскость или сфера. Выбор того или иного посредника зависит как от типа пересекаемых поверхностей, так и от их взаимного расположения.

Различают два вида пересечения поверхностей:

1)полное, когда все образующие или ребра одной поверхности соответственно пересекаются с другой поверхностью;2)частичное, когда честь образующих или ребер боковых поверхностей не участвуют в пересечении.

В результате полного пересечения получаются две замкнутые линии, а частичного – одна.

Построение линии пересечения начинают с нахождения её опорных точек. Промежуточные точки ищут в тех местах, где опорные точки расположены далеко друг от друга.

Линия пересечения двух поверхностей может быть:

1)пространственная ломаная линия – при пересечении двух многогранников;

2)пространственная кривая – при пересечении двух кривых поверхностей или кривой поверхности и многогранника.

 

Виды. Разрезы. Сечения.

Изображения предметов должны выполняться по методу прямоугольного проецирования. При этом предмет располагают между наблюдателем и соответствующей плоскостью проекций. За основные плоскости проекций принимают 6 граней куба. Главное изображение выбирают так, чтобы оно давало наиболее полное представление о форме и размерах предмета. Количество изображений на чертеже должно быть минимальным, но обеспечивающим полное представление о предмете.

	Вид снизу
Вид справа	Главный вид (вид спереди)	Вид слева	Вид сзади
	Вид сверху

Вид – изображение обращенной к наблюдателю видимой части поверхности предмета. Виды: основной, дополнительный, местный и развернутый. Основной вид – вид, который наиболее полно показывает форму поверхности предмета. Дополнительный вид – изображение предмета или его частей без искажения формы и размеров. Местный вид – изображение отдельного, ограниченного места поверхности предмета. Развернутый вид – изображение поверхностей некоторых предметов сложной формы. Названия видов не надписывают, если они расположены в установленной проекционной связи. Если проекционная связь нарушена, то направление проецирования должно быть указано стрелкой и прописной буквой. Разрез – изображение предмета, мысленно рассеченного одной (или несколькими) секущими плоскостями. В зависимости от положения секущей плоскости относительно плоскости проекций разрезы называют горизонтальными, вертикальными и наклонными. Горизонтальный разрез имеет секущую плоскость, параллельную горизонтальной плоскости проекций. Вертикальный разрез имеет секущую плоскость, горизонтальной плоскости проекций. Наклонный разрез имеет секущую плоскость, не параллельную и не горизонтальной плоскости проекций. Когда секущая плоскость совпадает с плоскостью симметрии предмета в целом, то положение секущей плоскости не обозначают и разрез надписью не сопровождают. Разрез обозначается, если секущая плоскость не является плоскостью симметрии предмета (например А – А).

Сечение - изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями (черт. 6). На сечении показывается только то, что получается непосредственно в секущей плоскости.

Образование конической поверхности. Сечения конической поверхности плоскостями.

КОНИЧЕСКИЕ СЕЧЕНИЯ - линия пересечения кругового конуса с плоскостями, не проходящими через его вершину. Конические сечения могут быть трех типов:

а) - секущая плоскость пересекает все образующие конуса в точках одной его полости; линия пересечения - замкнутая овальная кривая - эллипс, в частности, когда плоскость перпендикулярна оси конуса, - окружность;

б) - секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая - парабола, целиком лежащая в одной полости;

в) - секущая плоскость пересекает обе полости конуса; линия пересечения гипербола - состоит из двух одинаковых незамкнутых, простирающихся в бесконечность ветвей, лежащих на обеих полостях конуса.

 

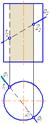
Образование цилиндрической поверхности. Сечения цилиндрической поверхности плоскостями.

В некоторой плоскости α рассмотрим окружность w(O,R) с центром в точке O и радиусом R. Через каждую точку окружности проведём прямую перпендикулярную плоскости α.

Цилиндрической поврехностью называется фигура образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности.

Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.

Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.

Образование сферической поверхности. Сечения сферической поверхности плоскостями.

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр.

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Точка и прямая в плоскости. Главные линии плоскости (горизонталь, фронталь).

Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (ΔКLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α ((ΔКLM), то пряма АВ, проходящая через эти точки, принадлежит плоскости α.

Горизонталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ, параллельную оси х.

Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости.

Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекцияф параллельна оси х.