
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции прямых общего и частного положенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ
Учебный процесс по начертательной геометрии включает следующие формы обучения: лекции, самостоятельную работу студентов (СРС), практические занятия, контроль знаний по темам курса, выполнение графических работ, экзамен. Лекции. На лекциях студенты получают основную информацию по теоретическим основам курса, знакомятся с методами решения задач. СРС. Теоретический материал углубленно изучается по рекомендованным учебникам и закрепляется решением упражнений, помещенных в этой тетради. Выполняются расчетно-графические работы по индивидуальным заданиям. Практические занятия. 1. Преподаватель проверяет задачи, самостоятельно решенные студентами и консультирует группу по материалу темы. 2. Проводится контроль знаний, оценивается степень подготовки студентов к практическим занятиям. 3. Решаются задачи из тетради или выполняются расчетно-графические работы. Рабочая тетрадь включает материал, обеспечивающий закрепление знаний по темам курса в процессе самостоятельной работы студентов, а также материалы, необходимые для проведения практических занятий и выполнения расчетно-графических работ. Учебный материал сгруппирован по практическим занятиям в соответствии с рабочей программой курса. В разделе для каждого практического занятия содержатся: 1. Краткие теоретические сведения и методические указания к изучаемой теме. 2. Упражнения для самостоятельного решения студентами после прослушанной лекции. 3. Условие задач, рекомендованных для решения на практических занятиях под руководством преподавателя. В рабочей тетради приняты обозначения: Точки обозначаются прописными буквами латинского алфавита (А, B, C, D,…), а также цифрами – 1, 2, 3,… Линии обозначаются строчными буквами латинского алфавита – а, b, с, d,… Плоскости обозначаются буквами греческого алфавита – a, b, g, e, p,… Плоскости проекций обозначаются: p1 – горизонтальная плоскость проекций, p2 – фронтальная плоскость проекций, p3 – профильная плоскость проекций. Проекции точек, линий, плоскостей обозначаются теми же буквами, что и оригиналы, только с индексами, соответствующими индексам плоскостям проекций – А 1, А 2... 11, 12,...
ТОЧКА И ЕЕ ПРОЕКЦИИ
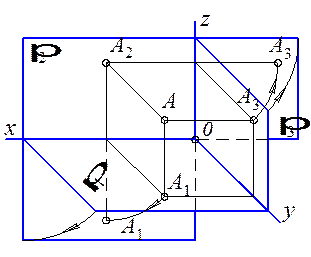
Модель проецирования точки Комплексный чертеж точки
Рис. 1.1 Рис. 1.2
Определитель точки пространства – координаты х, y, z точки, то есть расстояния точки от трех координатных плоскостей. Принимается, что плоскости проекций совмещены с координатными. Условная запись определителя точки: А (х, y, z). Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций. Комплексным чертежом называется плоский чертеж, состоящий из проекций изображаемого образа, размещенных в проекционной связи друг с другом. Линия проекционной связи всегда перпендикулярна оси проекций, разделяющие данные изображения. Комплексный чертеж точки содержит две проекции точки, связанные между собой линией проекционной связи. Для комплексного чертежа точки имеют такие положения: 1. Фронтальная и горизонтальная проекции точки всегда располагаются на вертикальной линии связи (А 2 А 1 ^ ох). 2. Фронтальная и профильная проекции точки всегда располагаются на горизонтальной линии связи (А 2 А 3 ^ оz). 3. Расстояние от фронтальной проекции точки до оси ох определяет высоту и определяется координатой z. Расстояние от горизонтальной проекции точки до оси ох определяет глубину точки и определяется координатой y. 4. По горизонтальной и фронтальной проекциям точки всегда можно построить ее профильную проекцию. Для этого на горизонтальной линии связи, проведенной через А 2, откладываются от оси оz координата y (координатным или графическим путем).
Контрольные вопросы 1. К каким проекциям относится ортогональная проекция точки? 2. Что такое чертеж точки? 3. Как получается чертеж в системе p1, p2, p3? 4. Как на чертеже определяется расстояние точки от плоскостей проекций p1, p2, p3? 5. При каком условии точки А и В находятся на одинаковом расстоянии от плоскости p3? 6. К какой из плоскостей проекции ближе всех расположена точка К (50, 30, 20)? 7. Сколько проекций точки определяют ее положение в пространстве? 8. При каком условии точка А будет равноудалена от плоскостей проекций p1, p2, p3?
Задачи
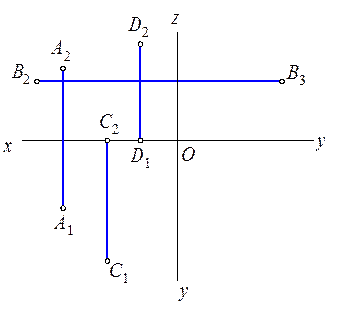
1.1.1. Построить чертеж точек: А (40, 15, 20); В (30, 30, 0); С (40, 0, 20); D (0, 30, 30). Построить наглядное изображение. 1.1.2. Построить третьи проекции т. А, В, С, D.
1.1.3. Построить третьи проекции т. А, В, С, D.
1.1.4. Построить третью проекцию точек. Измерить и записать координаты точек. Построить наглядное изображение точек.
1.1.5. Построить проекции точки В, расположенной на 20 мм выше плоскости p1 и на 15 мм ближе к плоскости p2, чем данная точка А.
1.1.6. Построить проекции точек А и В симметричных точке С (20, 15, 30) относительно плоскости p1 и начала координат.
1.1.7. По проекции А 2 построить проекции А 2 и А 3 так, чтобы z =
1.1.8. По проекции В 3 построить проекции А 1и А 2 так, чтобы y = 2 x (В 3 - произвольно).
ПРОЕЦИРОВАНИЕ ПРЯМОЙ
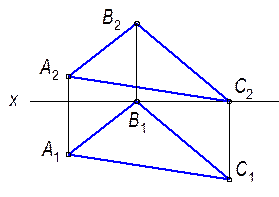
Рис. 2.3. НВ отрезка прямой
- Определитель прямой: две точки (АВ) или отрезок (l). - Точка принадлежит прямой, если проекции точки принадлежат одноименным проекциям прямой. - Проекциями прямой, в общем случае, являются прямые линии. - Точки пересечения прямой с плоскостями проекций называются следами прямой и определяются как особые точки прямой, одна из координат которых равна нулю. - Натуральная величина (НВ ) отрезка прямой общего положения определяется величиной гипотенузы прямоугольного треугольника, построенного на одной из проекций, как на катете. Второй катет треугольника равен разности расстояний концов отрезка от той плоскости проекций, на которой взят первый катет.
Задачи
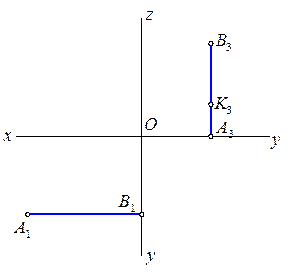
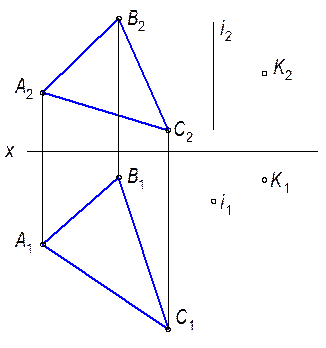
2.2.1. Построить на эпюре третью проекцию прямой и недостающие проекции принадлежащей ей точки К.
2.2.2. Построить на прямой точки: А с координатой z = 25мм. В с координатой z = 0мм. С с координатой y = 20мм.
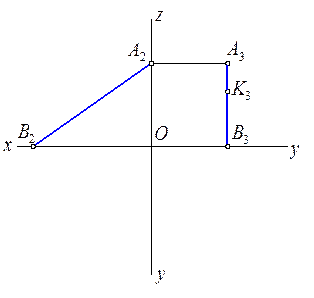
2.2.3. Дана ломанная линия ABCDE. Найти натуральную величину (НВ) этой ломанной линии. Построить на отрезке CD точку К, если СК = 15мм.
2.2.4. Определить натуральную величину (НВ ) отрезка АВ и угол
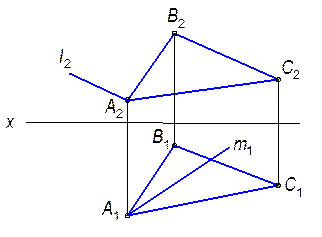
2.2.5. На прямой l отложить отрезок АВ = 30мм.
2.2.6. Построить проекции точки С принадлежащей прямой АВ и удаленной от плоскости p2 на 25мм.
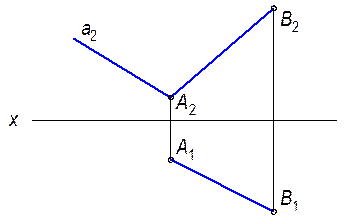
2.2.7. Построить фронтальную проекцию точки А, отстоящей от точки В на 40мм.
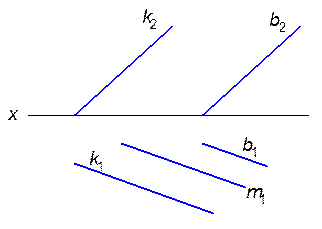
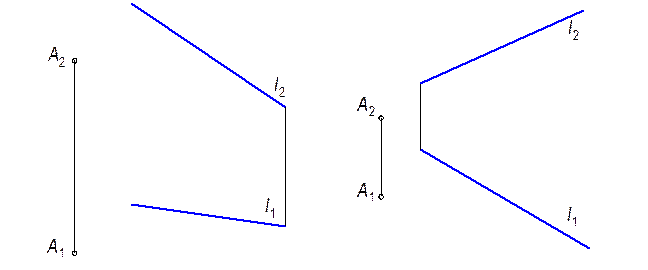
2.2.8. Через точку М провести прямую l, параллельную прямой k.
2.2.9. Через точку А провести прямую АВ, параллельную прямой KL.
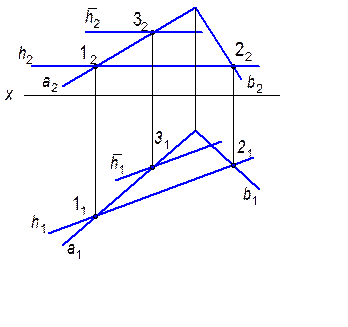
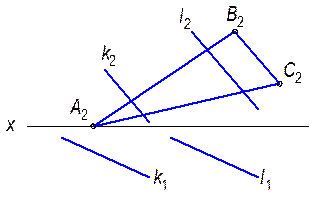
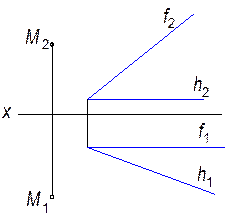
2.2.10. Через точку А провести горизонтальную прямую h, пересекающую прямую k.
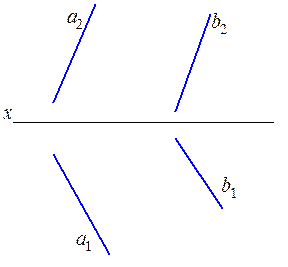
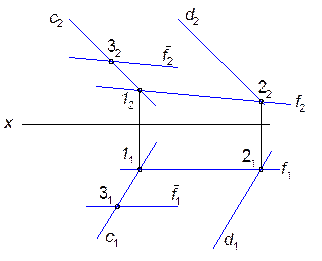
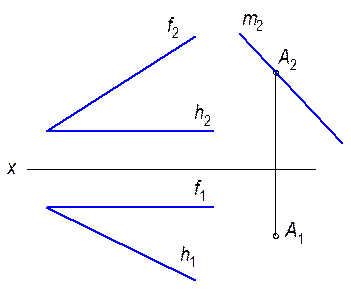
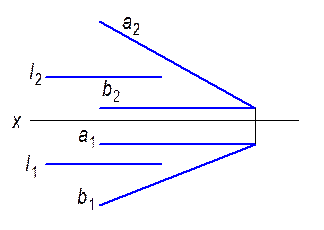
2.2.11. Провести фронтальную прямую f, находящуюся от плоскости p2 на расстоянии 25мм и пересекающую параллельные прямые a и b.
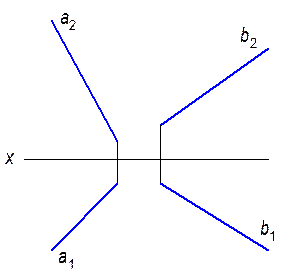
2.2.12. Через точку М провести прямую k, пересекающую прямую а и ось z.
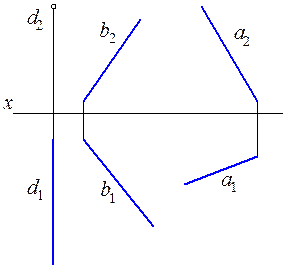
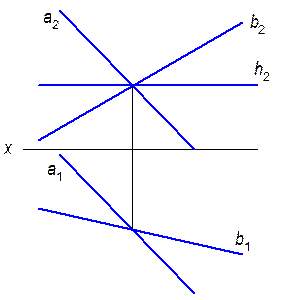
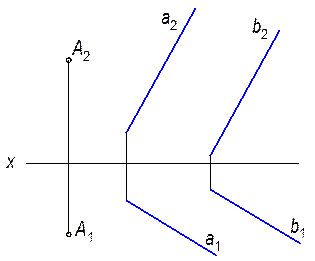
2.2.13. Построить проекции прямой, параллельной прямой a и пересекающей прямые b и d.
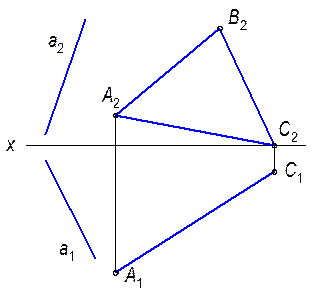
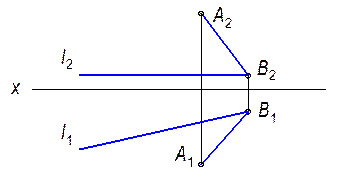
2.2.14. Через точку Е провести прямую, пересекающую прямые АВ и CD.
2.2.15. Построить проекции равнобедренного
2.2.16. АС диагональ ромба ABCD. В
ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ
Рис. 3.1. Модель плоскости Рис. 3.2. Чертеж плоскости
1. На чертеже плоскость может быть задана: проекциями трех точек, не лежащих на одной прямой; проекциями прямой и точки вне этой прямой; проекциями параллельных прямых; проекциями пересекающихся прямых; проекциями плоской фигуры; следами. 2. Прямая принадлежит плоскости, если она проведена через две точки, заведомо лежащие в этой плоскости или проходит через одну и параллельна прямой, лежащей в этой плоскости.
3. Точка принадлежит плоскости, если она построена на прямой, принадлежащей заданной плоскости. 4. По отношению к плоскости проекций плоскости разделяются на плоскости общего положения и плоскости частного положения – проецирующие (перпендикулярные к одной из плоскостей проекций) и уровня (параллельные к одной из плоскостей проекций). 5. В плоскости можно провести линии уровня (горизонталь, фронталь, профильная прямая), линию наибольшего наклона к каждой из плоскостей проекций.
Рис. 3.3. Горизонталь Рис. 3.4. Фронталь
Задачи
3.1.1. Построить l 1 и m 2 прямых, лежащих в плоскости
3.1.2. Построить m 2 прямой m, лежащей в плоскости a(k çç l).
3.1.3. Построить горизонтальную проекцию
3.1.4. Построить профильную проекцию
3.1.5. Построить D 2 и E 1 точек D и E, принадлежащих плоскости a(а çç b).
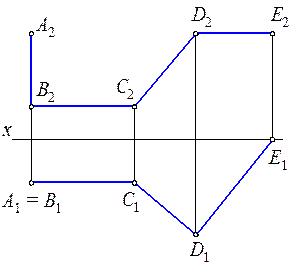
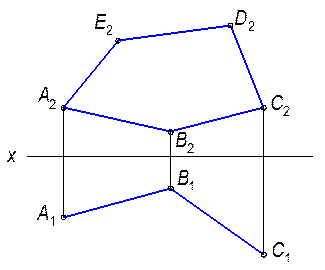
3.1.6. Построить горизонтальную проекцию пятиугольника A 1 B 1 C 1 D 1 E 1 по фронтальной проекции и горизонтальной проекции двух смежных сторон А 1 В 1 С 1.
3.1.7. Построить горизонтальную проекцию
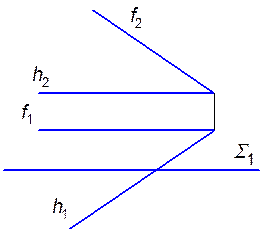
3.1.8. Провести в каждой из заданных плоскостей горизонталь (h) на расстоянии 15 мм от p1 и фронталь (f) на расстоянии 20 мм от p2.
3.1.9. В плоскости a(а Ç b) построить недостающую проекцию горизонтали (h 1).
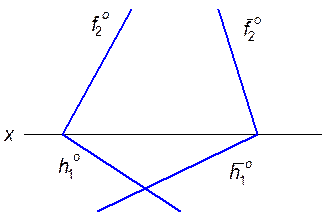
3.1.10. Построить горизонтальный след плоскости a, заданной фронтальным следом f 0 и точкой А.
3.1.11. Определить горизонтальную проекцию прямой m, проходящей через точку А и параллельную плоскости a(f Ç h).
3.1.12. Через прямую а провести плоскость a параллельную прямой b.
3.1.13. Построить проекции горизонтальной прямой, параллельной плоскости a(а çç b) и проходящей через точку А.
3.1.14. Построить горизонтальную проекцию
3.1.15. Построить горизонтальную проекцию
3.1.16. Через точку М провести профильную прямую (M - N), параллельную плоскости å(f Ç h).
3.1.17. Через точку А провести плоскость å, параллельную прямой.
а)
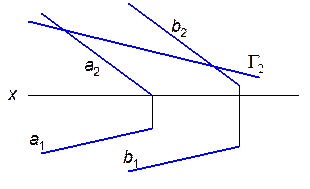
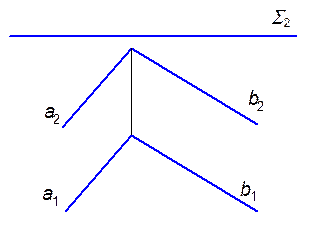
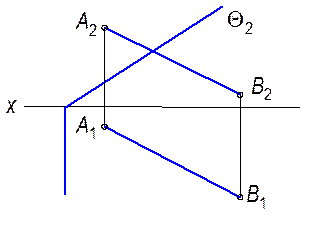
Задачи 4.1.1. Построить линию пересечения плоскости å (а çç b) с плоскостью (Г^ p2).
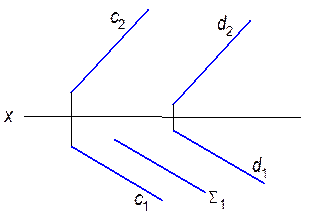
4.1.2. Построить линию пересечения плоскости a(c çç d) с плоскостью å(å ^ p1).
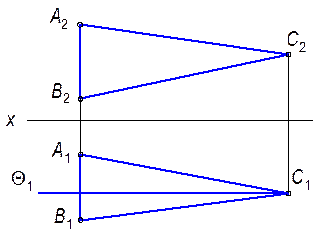
4.1.3. Построить линию пересечения плоскости Г(АВС) с плоскостью q(q ^ p1).
4.1.4. Построить линию пересечения плоскости Г(а Ç b) с плоскостью a(c çç d).
4.1.5. Построить линию пересечения плоскости a(f 0Ç h 0) с плоскостью b(` f 0Ç` h 0).
4.1.6. Найти линию пересечения двух плоскостей:
Задачи 5.1.1. Построить точку пересечения прямой АВ с плоскостью (q ^ p2).
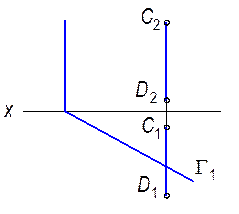
5.1.2. Построить точку пересечения прямой СD и плоскостью Г(Г ^ p1).
5.1.3. Построить проекции точки пересечения прямой m c плоскостью
5.1.4. Построить точку пересечения прямой m с плоскостью S(f Ç h).
5.1.5. Построить точку пересечения прямой l с плоскостью a (а Ç b).
5.1.6. Построить точку пересечения прямой а с плоскостью
Задачи
6.1.1. Построить проекции равнобедренного ∆ АВС, если СМ (СМ êêp1) высота А Î p1; В Î p2.
6.1.2. Построить проекции ромба АВСD, если АС (АС êêp2) диагональ ромба, В Î p1; D – равноудалена от плоскостей p1 и p2.
6.1.3. Построить проекции ∆ АВС с прямым углом при вершине А, гипотенуза ВС которого лежит на прямой l.
6.1.4. Через точку А провести проекции прямой, перпендикулярной к плоскости å (f Ç h).
6.1.5. Через точку А провести проекции прямой, перпендикулярной к плоскости ∆ (АВС).
6.1.6. Через точку К провести проекции перпендикуляра к плоскости å (а Ç b).
6.1.7. Через точку А провести проекции плоскости, перпендикулярной к прямой ВС.
6.1.8. В точке М пересечения медиан (центр тяжести) ∆ АВС провести перпендикуляр к его плоскости.
МНОГОГРАННИКИ Если все точки линии принадлежат поверхности, то линия принадлежит поверхности. Если точка принадлежит линии, а линия поверхности, то точка принадлежит поверхности.
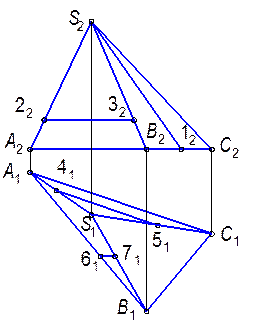
Задачи 7.1.1. Построить недостающие проекции точек, принадлежащих поверхностям геометрических фигур.
7.1.2. Построить недостающие проекции линий, принадлежащих поверхностям геометрических фигур.
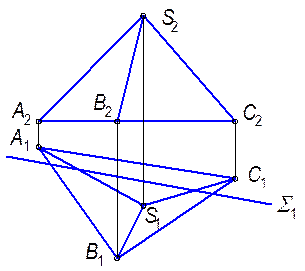
7.1.3. Построить линию пересечения пирамиды с плоскостью.
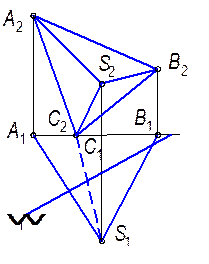
7.1.4. Построить линию пересечения плоскости с геометрическими фигурами.
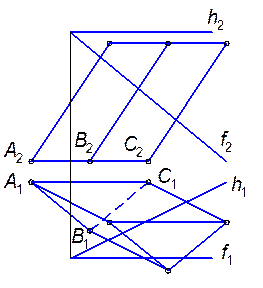
7.1.5. Построить точки пересечения прямой с геометрическими фигурами.
7.1.6. Построить линию пересечения двух многогранников и определить видимость.
СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА
Способы преобразования комплексного чертежа позволяют преобразовывать прямые и плоскости общего положения в частное положение относительно плоскостей проекций, что облегчает решение позиционных и метрических задач. Задачи
5.1.3.1. Найти горизонтальную проекцию отрезка AB, длина которого 45 мм.
8.1.3.2. Найти фронтальную проекцию точки К 1, отстоящей от горизонтали h на 20 мм.
8.1.3.3. Определить расстояние от точки М до плоскости
8.1.3.4. Определить углы наклона прямой АВ к плоскостям проекций
8.1.3.5. Определить расстояние между параллельными плоскостями
8.1.3.6. Определить углы наклона плоскости
8.1.3.7. Определить расстояние между параллельными прямыми a и b.
8.1.3.8. Определить расстояние от точки М до прямой а.
8.1.3.9. Построить проекции прямоугольного равнобедренного
8.1.3.10. Найти горизонтальную проекцию точки D, равноудаленной от вершин заданного треугольника АВС.
8.1.3.11. Найти горизонтальную проекцию прямой СD, параллельной прямой АВ, если известно, что расстояние между ними равно 20мм. Указать количество решений.
8.1.3.12. Провести прямую m, параллельной двум заданным прямым а и b и удаленную от прямой a на 20мм и от прямой b на 15мм. Указать количество решений.
8.1.3.13. Построить проекции квадрата ABCD по данной его стороне АВ и направлению а 2 фронтальной проекции смежной с АВ стороны АD.
Способ вращения Способ вращения заключается в том, что геометрический объект вращают вокруг некоторой оси до требуемого положения относительно плоскостей проекций. При этом все точки объекта описывают дуги окружностей в плоскостях, перпендикулярных оси вращения. Центры этих дуг располагаются на оси вращения, а радиусы равны кратчайшему расстоянию от вращаемых точек до оси. Оси вращения располагают параллельно или перпендикулярно одной из плоскостей проекций.
Рис. 8.2.2.1
Пусть точка А вращается вокруг оси i, перпендикулярной горизонтальной плоскости проекции (рис. 91). Вращаясь, точка А будет описывать окружность в плоскости, перпендикулярной оси вращения и, следовательно, параллельной горизонтальной плоскости проекций Таким образом, при вращении точки вокруг проецирующей прямой на плоскости перпендикулярной оси вращения, проекция точки перемещается по дуге окружности, а на плоскости, параллельной оси вращения - по прямой линии, параллельной оси ox. Вращение прямой линии и плоскости сводится к вращению на один и тот же угол двух точек, принадлежащих прямой, а вращение плоскости – трех ее точек, не лежащих на одной прямой. Пример 1: Повернем прямую общего положения АВ до положения горизонтали. Выберем ось вращения i, проходящую через точку А и перпендикулярную плоскости
Рис. 8.2.2.2
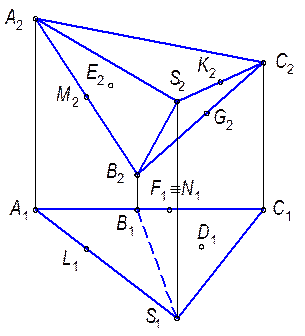
Пример 2: Повернем плоскость общего положения Горизонталь фронтально-проецирующей плоскости является фронтально-проецирующей прямой. Поэтому в плоскости Ось вращения проведем через вершину А, следовательно она при вращении остается неподвижной и достаточно повернуть две другие вершины
Рис. 8.2.2.3
Задачи
Задачи 8.2.4.1 – 8.2.4.4 ориентированны на метод решения способом вращения вокруг линии уровня, а остальные на способ вращения вокруг проецирующей прямой и плоско- параллельного перемещения. 8.2.4.1. Определить натуральную величину
8.2.4.2. Определить натуральную величину угла между прямыми а и b.
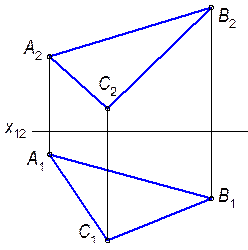
8.2.4.3. Определить натуральную величину параллелограмма ABCD.
8.2.4.4. Построить проекции квадрата ABCD, вершина D которого лежит на прямой а. Определить натуральную величину квадрата.
8.2.4.5. Определить расстояние от точки D до плоскости
8.2.4.6. Найти центр описанной вокруг
8.2.4.7. Определить угол наклона прямой AD к плоскости
8.2.4.8. Повернуть точку М вокруг оси i до совмещения с плоскостью
8.2.4.9. Плоскость
8.2.4.10. Построить проекции квадрата ABCD, вершина D, которого принадлежит прямой а.
Задачи
9.1.1. Построить проекции цилиндра, заданного его основанием и горизонтальной проекцией образующей А 1 В 1. Точка М лежит на поверхности цилиндра.
9.1.2. Построить проекции сферы, если даны проекции центра сферы 0 и точки М, лежащей на этой сфере.
9.1.3. Построить проекции конуса вращения с вершиной в данной точке S и основанием лежащим в плоскости
9.1.4. Построить проекции конуса вращения, ось которого лежит на прямой а. Высота конуса равна l, окружность основания касается плоскости
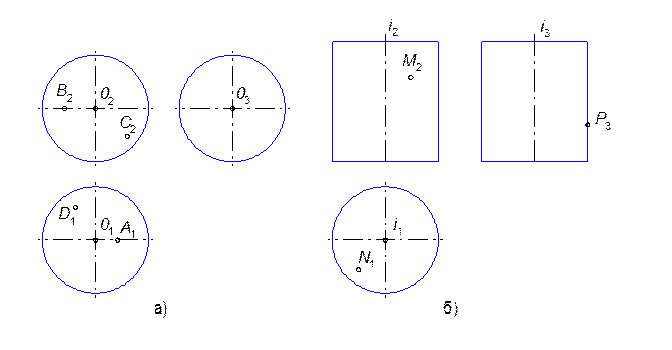
9.1.5. Найти недостающие проекции точек A,B,C,D на поверхности сферы (а); M,N,P на поверхности цилиндра (б); E,F,K,L на поверхности тора (в).
9.1.6. Построить фронтальную проекцию линии АВ на поверхности конуса вращения (а); горизонтальную проекцию линии MN на поверхности наклонного цилиндра (б); горизонтальную и профильную проекции линий АВС на поверхности сферы (в).
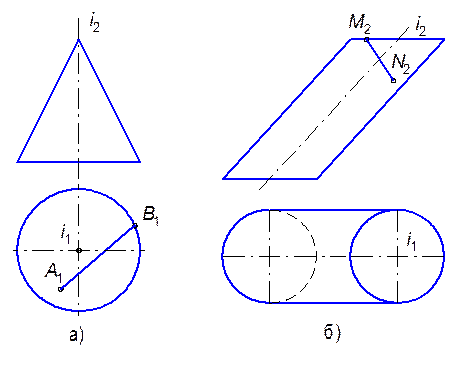
9.1.7. Поворотом вокруг оси i точку А совместить с поверхностью сферы (а), а точку В - с поверхностью тора (б).
Задачи
10.1.1. Построить недостающую проекцию цилиндра вращения и построить его сечение плоскостью
10.1.2. Построить сечение заданного цилиндра плоскостью
10.1.3. Построить профильную проекцию цилиндра и его сечение горизонтальными и профильными плоскостями.
10.1.4. Рассечь данный цилиндр плоскостью, параллельной его оси и наклоненной к плоскости
10.1.5. Построить проекции и натуральную величину сечения цилиндра плоскостью
10.1.6. Построить проекции и натуральную величину сечения конуса вращения плоскостью
10.1.7. Построить сечение конуса плоскостью
10.1.8. Дана прямая а 1 лежащая в основании конуса. Построить плоскость
10.1.9. Построить проекции и натуральную величину сечения конуса плоскостью
10.1.10. Построить горизонтальную и профильную проекции сечения конуса вращения горизонтальными и фронтально- проецирующими плоскостями.
10.1.11. Построить сечения сферы плоскостью, заданной прямой а и точкой А на поверхности сферы.
10.1.12. Построить на сфере кратчайшее расстояние между точками А и В на ней.
10.1.13. Построить горизонтальную и профильную проекции сечения сферы горизонтальными и профильными плоскостями.
10.1.14. Построить проекции и натуральную величину сечения тора плоскостью
Задачи 11.1.1. Определить точки пересечения прямой m с поверхностью сферы.
11.1.2. Определить точки пересечения прямой m с поверхностью цилиндра.
11.1.3. Определить точки пересечения прямой m с поверхностью конуса.
11.1.4. Определить точки пересечения прямой m с поверхностью тора.
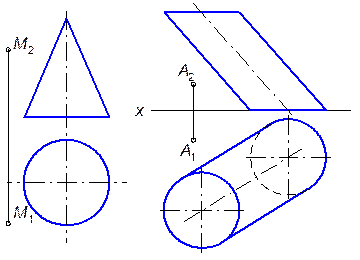
11.1.5. Определить кратчайшее расстояние от точки М до поверхности конуса (а) и от точки А до поверхности цилиндра (б).
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Рис. 12.5
Задачи
12.3.1. Построить проекции линии пересечения сферы и призмы.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.88.161 (0.013 с.) |





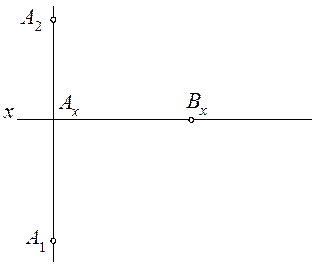

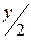 (А 2 - произвольно).
(А 2 - произвольно).


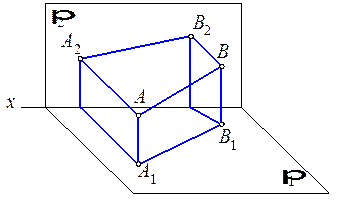
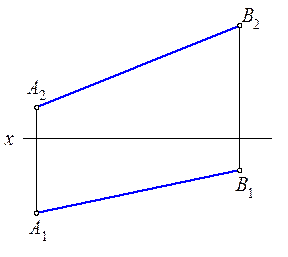

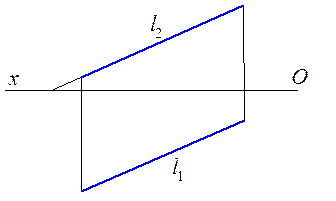
 Рис. 2.1. Проекция прямой Рис. 2.2. Следы прямой
Рис. 2.1. Проекция прямой Рис. 2.2. Следы прямой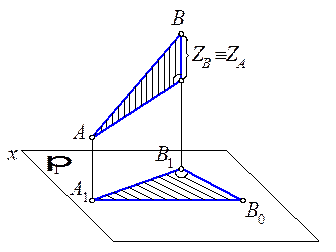


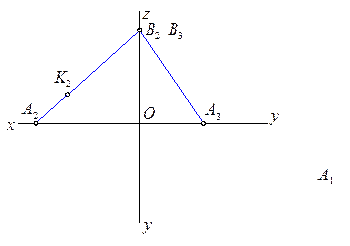



 наклона его к плоскости проекций p1.
наклона его к плоскости проекций p1.

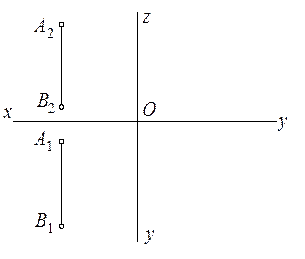
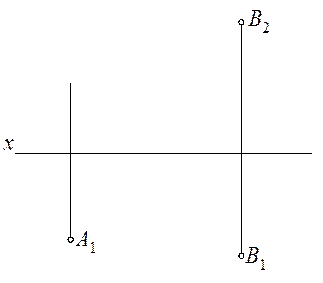
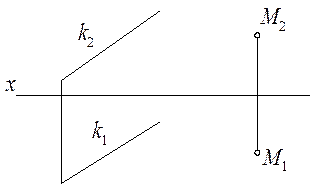




 АВС. Если СМ – высота
АВС. Если СМ – высота 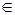 p1; B
p1; B 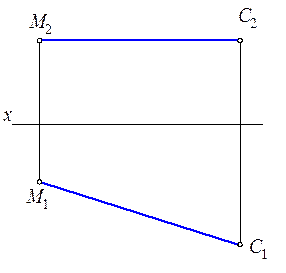


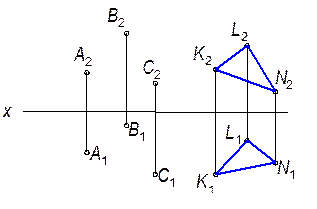




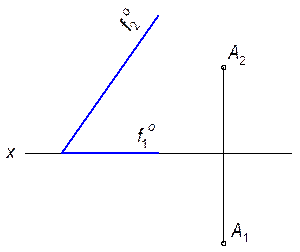
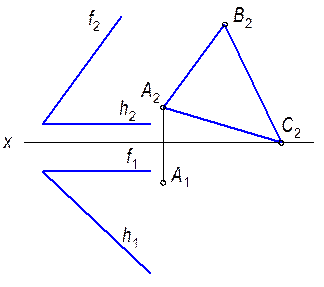
 б)
б) 












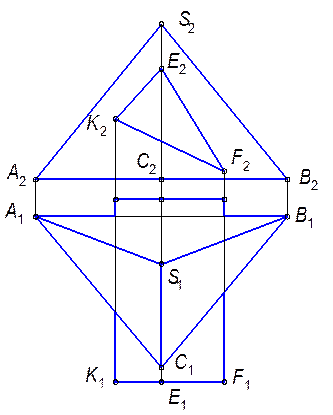


 (АВС).
(АВС).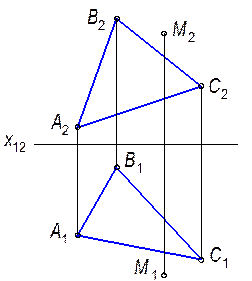
 и
и 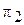 .
.
 и
и  .
.
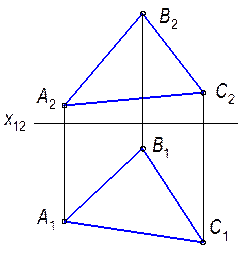


 АВС, катет АВ которого принадлежит прямой а. Угол при вершине А – прямой.
АВС, катет АВ которого принадлежит прямой а. Угол при вершине А – прямой.



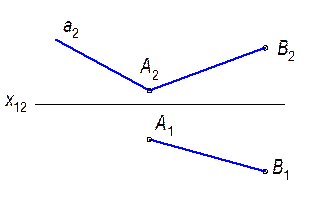
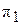 . Поэтому на плоскость
. Поэтому на плоскость 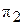 - в виде отрезка, параллельного плоскости
- в виде отрезка, параллельного плоскости 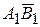 отражает натуральную величину отрезка АВ, а угол между
отражает натуральную величину отрезка АВ, а угол между 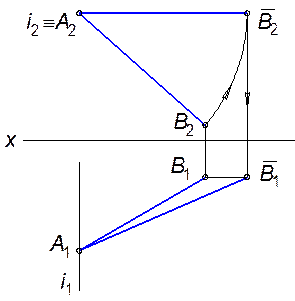
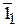 . Точка
. Точка 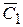 лежит на пересечении дуги радиуса А 1 С 1 и продолжения прямой
лежит на пересечении дуги радиуса А 1 С 1 и продолжения прямой 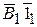 . Фронтальные проекции точек В и С перемещаются по линиям параллельным оси ox, до пересечения с соответствующими линиями связи от точек
. Фронтальные проекции точек В и С перемещаются по линиям параллельным оси ox, до пересечения с соответствующими линиями связи от точек  и
и  ) позволяет определить угол наклона плоскости
) позволяет определить угол наклона плоскости 



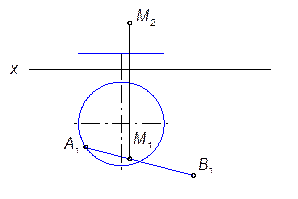

 . Радиус основания равен высоте конуса.
. Радиус основания равен высоте конуса.
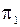 .
.



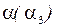 .
.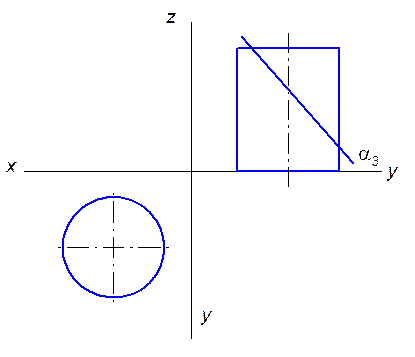

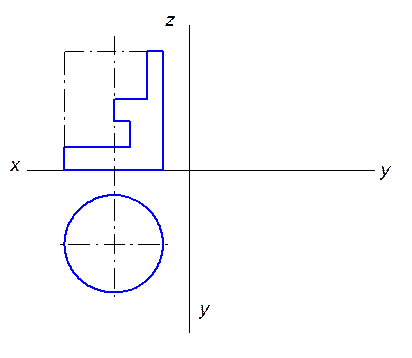
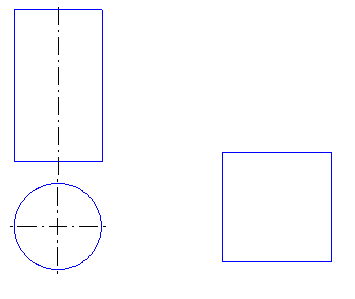
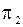 под углом 450 так, чтобы сечение было равновелико данному квадрату. Указать количество решений.
под углом 450 так, чтобы сечение было равновелико данному квадрату. Указать количество решений.
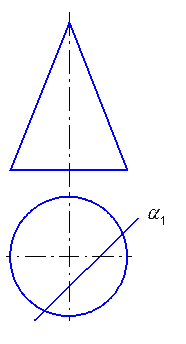
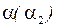 .
.
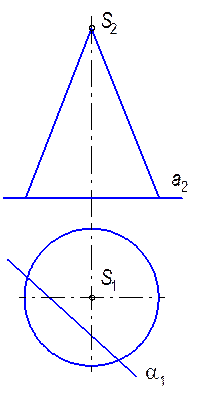



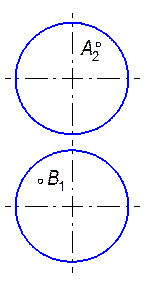


 a) б)
a) б)
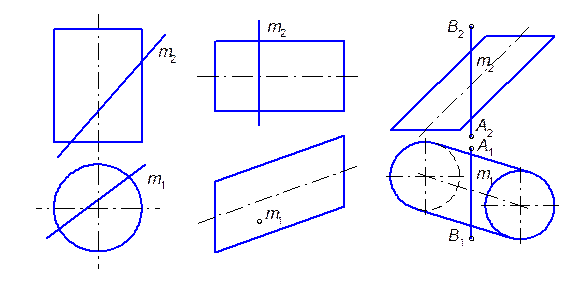 а) б) в)
а) б) в)
 а) б) в)
а) б) в)

 а) б)
а) б)




