Положение плоскостей относительно плоскостей проекций

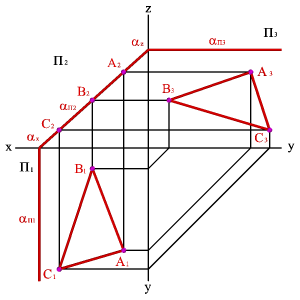
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальныйa_П1; - фронтальный a_П2; - профильный a_П3).

2. Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (a ^П₁), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом (рис. 29).

 

 

а) модель	б) эпюр
Рисунок 29. Горизонтально проецирующая плоскость

 

2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (a^П ₂)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом a_П2 (рис. 30).

 

 

а) модель	б) эпюр
Рисунок 30. Фронтально проецирующая плоскость

 

2.3. Плоскость, перпендикулярная профильной плоскости (a^П ₃) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис. 31).

 

а) модель	б) эпюр
Рисунок 32. Биссекторная плоскость

 

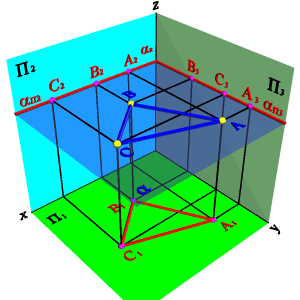
3. Плоскости, параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельна исследуемая плоскость, различают:

3.1. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций (aП ₁) - (a^П₂,a^П₃). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₁ без искажения, а на плоскости П₂ и П₃ в прямые - следы плоскости a_П2 и a_П3 (рис. 33).

 

а) модель	б) эпюр
Рисунок 33. Горизонтальная плоскость

3.2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (aП₂), (a^П₁, a^П₃). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₂ без искажения, а на плоскости П ₁ и П ₃ в прямые - следы плоскости a_П1 и a_П3 (рис. 34).

а) модель	б) эпюр
Рисунок 34. Фронтальная плоскость

 

3.3 профильная плоскость – плоскость, параллельная профильной плоскости проекций (a//П₃), (a^П₁, a^П₂). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₃ без искажения, а на плоскости П₁ и П₂ в прямые - следы плоскости a_П1 и a_П2 (рис. 35).

а) модель	б) эпюр
Рисунок 35. Профильная плоскость

3.5. Отображение относительного положения двух плоскостей

Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

 

Параллельные плоскости

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Это определение хорошо иллюстрируется задачей: через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми (a, b) (рис. 36).

а) модель	б) эпюр
Рисунок 36. Параллельные плоскости

Для решения задачи требуется через точку В провести плоскость, параллельную плоскости (a, b) и задать её двумя пересекающимися прямыми c и d.

Для того, чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой.

Пересекающиеся плоскости

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис. 37).

Дано: плоскость общего положения, заданная треугольником АВС, а вторая плоскость - горизонтально проецирующая a. Требуется построить линию пересечения заданных плоскостей.

Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью a - точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как a - горизонтально проецирующая плоскость, то проекция D₁F₁ совпадает со следом плоскости a_П1 таким образом остается только построить недостающие проекции DF на П₂ и П₃.

а) модель	б) эпюр
Рисунок 37. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью

 

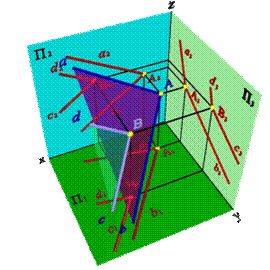
Рассмотрим общий случай пересечения плоскостей, когда плоскости занимают общее положение в пространстве.

Дано: Две плоскости общего положения a()n,m и b (ABC) (рис. 38). Требуется построить линию пересечения плоскостей a и b.

а) модель	б) эпюр
Рисунок 38. Пересечение плоскостей общего положения

 

 

Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с заданными плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точкапересечения этих прямых- К,которая одновременно принадлежит трем плоскостям a, b и g,т.е. искомой линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C), точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом, прямая (КМ) является линией пересечения плоскостей a и b.