Кривые поверхности. Классификация поверхностей.

Проецирование поверхностей

В начертательной геометрии поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию, перемещающуюся в пространстве и образующую поверхность, называют образую­щей. Образующие могут быть прямыми и кривыми. Образующие поверхность кривые могут быть постоянными и переменными, например закономерно изменяющимися.

Одна и та же поверхность в ряде случаев может рассматривать­ся как образованная движениями различных образующих. На­пример, круговой цилиндр может быть образован: во-первых, вращением прямой относительно неподвижной оси, параллель­ной образующей; во-вторых, движением окружности, центр ко­торой перемещается по прямой, перпендикулярной плоскости окружности; в-третьих, прямолинейным движением сферы.

При изображении поверхности на чертеже показывают лишь некоторые из множества положений образующей. На рисун­ке 49 показана поверхность с образующей АВ. При своем движении образующая остается параллельной выбранному направ­лению MN одновременно пересекает некоторую кривую линию CDE. Таким образом движение обра­зующей АВ направляется в простран­стве линией CDE.

Рисунок 49	Рисунок 50

Линию или линии, пересечение с которыми является обязательным ус­ловием движения образующей при образовании поверхности, называют направляющей или направляющими. На рисунке 50 показана проекция поверх­ности, образованной движением пря­мой АВ по двум направляющим — прямой О₁О₂ и пространственной кривой FGQ, не пересекающей прямую О₁О₂.

Иногда в качестве направляющей исполь­зуют линию, по которой движется некото­рая характерная для образующей точка, но не лежащая на ней, например центр окруж­ности.

Из различных форм образующих, направ­ляющих, а также закономерностей образова­ния конкретной поверхности выбирают те, которые являются наиболее простыми и удоб­ными для изображения на чертеже поверхнос­ти и решения задач, связанных с нею.

Иногда для задания поверхности используют понятие опре­делитель поверхности, под которым подразумевают совокуп­ность независимых условий, однозначно задающих поверхность. В числе условий, входящих в состав определителя, различают геометрическую часть (точки, линии, поверхности) и закон (алгоритм) образования поверхности геометрической частью оп­ределителя.

Рассмотрим краткую классификацию кривых поверхностей, принятую в начертательной геометрии.

Линейчатые развертываемые поверхности. Поверхность, ко­торая может быть образована движением прямой линии, назы­вают линейчатой поверхностью. Если линейчатая поверхность может быть развернута так, что всеми своими точками она со­вместится с плоскостью без каких-либо повреждений поверхно­сти (разрывов или складок), то ее называют развертываемой. К развертываемым поверхностям относятся только такие линей­чатые поверхности, у которых смежные прямолинейные образу­ющие параллельны, или пересекаются между собой, или являются касательными к некоторой заданной пространствен­ной кривой. Все остальные линейчатые и все нелинейчатые по­верхности относятся к неразвертываемым поверхностям.

Рисунок 51 Рисунок 52 Рисунок 53

 

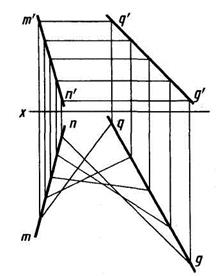
Развертываемые поверхности — цилиндрические, конические, с ребром возврата или торсовые. У цилиндрической поверхности образующие всегда параллельны, направляющая — одна кривая линия. Изображение на чертеже ранее показанной в простран­стве цилиндрической поверхности (см. рисунок 49) представлено на рисунке 51. Частные случаи — прямой круговой цилиндр, наклонный круговой цилиндр. У конических поверхностей все прямолинейные образующие имеют общую неподвижную точ­ку — вершину, направляющая — одна любая кривая линия. При­мер изображения конической поверхности на чертеже — рису­нок 52, проекции вершины s', s, направляющей c'd'e' cde. Частные случаи — прямой круговой конус, наклонный круговой конус. У поверхностей с ребром возвра­та или торсовых прямолинейные образующие касательны к одной криволинейной направляющей.

Линейчатые неразвертываемые поверхности: цилиндроид, коноид, гиперболический параболоид (косая плоскость). Повер­хность, называемая цилиндроидом, образуется при перемеще­нии прямой линии, во всех своих положениях сохраняющей па­раллельность некоторой заданной плоскости («плоскости параллелизма») и пересекающей две кривые линии (две направ­ляющие). Поверхность, называемая коноидом, образуется при перемещении прямой линии, во всех своих положениях сохраня­ющей параллельность некоторой плоскости («плоскости паралле­лизма») и пересекающей две направляющие, одна из которых кривая, а другая прямая линия (рисунок 53). Плоскостью параллелизма на рисунке 53 является плоскость Н, направляющие — кривая с проекциями a'g'q', agq, прямая с проекциями о₁’о₂’, о₁ о₂. В частном случае, если криволи­нейная направляющая — цилиндрическая винтовая линия с осью, совпадающей с прямолинейной направляющей, образу­емая поверхность — винтовой коноид, рассматриваемый ниже.

Рисунок 54	Рисунок 55

 

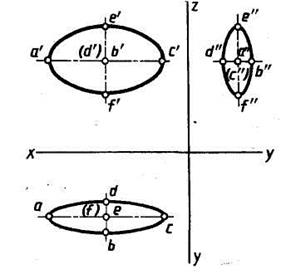
Чертеж гиперболического парабо­лоида, называемого косой плос­костью, приведен на рисунке 54. Образование этой поверхности можно рассматривать как резуль­тат перемещения прямолинейной образующей по двум направляю­щим — скрещивающимся прямым параллельно некоторой плоскости параллелизма. На рисунке 54 плоскость параллелизма — плос­кость проекций Н, направляю­щие — прямые с проекциями т'п' тп и q'g', qg.

Нелинейчатые поверхности. Их подразделяют на поверхнос­ти с постоянной образующей и поверхности с переменной обра­зующей.

Поверхности с постоянной образующей в свою очередь подразделяют на поверхности вращения с криволинейной об­разующей, например сфера, тор, эллипсоид вращения и др., и на цик­лические поверхности, напри­мер поверхности изогнутых труб постоянного сечения, пружин.

Поверхности с переменной образующей подразделяют на по­верхности циклические с переменной образующей, топографи­ческие поверхности аффинных и подобных линий и т. д. Чертеж поверхности второго порядка — эллипсоида — приведен на ри­сунке 55. Образующая эллипсоида — деформирующийся эл­липс, одна из проекций которого, например, d"e"b"f". Две направляющие — два пересекающихся эллипса, плоскости ко­торых ортогональны и одна ось общая, например с проекциями a'e'c'f' и adcb. Образующая пересекает направляющие в край­них точках своих осей. Плоскость образующего эллипса при пе­ремещении остается параллельной плоскости, образованной двумя пересекающимися осями направляющих эллипсов. Циклические поверхности с переменной образующей имеют образу­ющую — окружность переменного радиуса, направляющую — кри­вую, по которой перемещается центр образующей, плоскость образующей перпендикулярна к направляющей.

Каркасную поверхность задают некоторым множеством ли­ний или точек поверхности. Обычно такие линии — плоские кривые, плоскости которых параллельны между собой. Два пересекающихся семейства линий каркаса образуют сетчатый каркас поверхности. Точки пересечения линий образуют то­чечный каркас поверхности. Точечный каркас поверхности может быть задан и координатами точек поверхности. Каркас­ные поверхности широко используют при конструировании корпусов судов, самолетов, автомобилей, баллонов электрон­но-лучевых трубок. Из указанных поверхностей рассмотрим более подробно вин­товую.

Винтовые поверхности. Винтовые поверхности весьма широко используют в техни­ке для формообразования деталей различного назначения. Винтовая поверхность образуется при движении прямоли­нейной образующей по двум направляющим, одна из которых винтовая линия, другая — ось винтовой линии, которую обра­зующая пересекает под постоянным углом.

Прямая винтовая поверхность. У прямой винтовой поверх­ности угол между образующей и осью равен 90°. Это винто­вой коноид или прямой геликоид. Чертеж прямой винтовой поверхности приведен на рисунке 56. Перемещаясь в направ­лении, как указано стрелкой на горизонтальной проекции, отрезок АВ движется вдоль оси вверх и образует правую вин­товую поверхность.

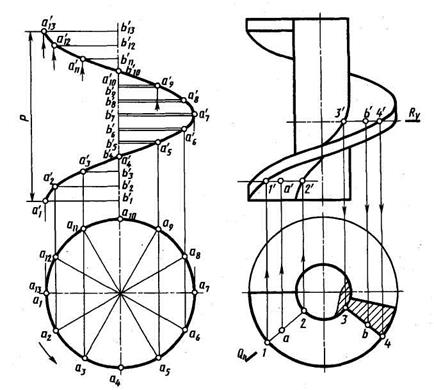
В сечении прямой винтовой поверхности (рисунок 57) плоско­стями, перпендикулярными оси или проходящими через ось, получаются отрезки прямолинейной образующей. Используя их, можно построить точки на винтовой поверхности. Так, на ри­сунке 69 по горизонтальной проекции а точки А построена ее фронтальная проекция а' на фронтальной проекции образующей 1'2' в секущей плоскости Q (Qh). По фронтальной проекции b' точки В построена ее горизонтальная проекция b на горизон­тальной проекции образующей 3—4 всекущей плоскости R.

Косая винтовая поверхность. Если у винтовой поверхности угол между образующей и осью не равен 90°, то ее называют косой винтовой поверхностью. Изображение косой винтовой поверхности — наклонного геликоида приведено на рисун­ке 70, а. Проекции отрезка АО — образующей изображены в ряде последовательных положений: от первого до тринадца­того. Точка А образующей перемещается по винтовой линии. Соответствующие положения проекций точки О отмечают на оси, руководствуясь тем, что проекция отрезка АО на ось вра­щения постоянна по величине.

 

Рисунок 56 Рисунок 57

 

 

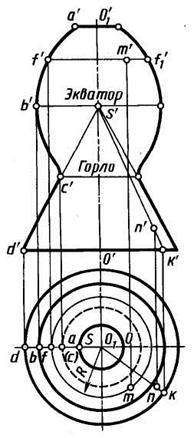
Поверхности вращения. Поверхности вращения и ограничиваемые ими тела имеют широкое применение во многих областях техники. В зависимости от вида образующей поверхности вращения могут быть ли­нейчатыми, нелинейчатыми или состо­ять из частей таких поверхностей.

Поверхностью вращения называют поверхность, получающуюся от враще­ния некоторой образующей линии вокруг неподвижной прямой— оси поверхности. Образующая линия может в общем случае иметь как кри­волинейные, так и прямолинейные участки. Поверхность вращения на чер­теже можно задать образующей и по­ложением оси. На рисунке 58 изоб­ражена поверхность вращения, которая образована вращением образующей вокруг оси ОО₁, перпендикулярной плоскости Н. При вращении каждая точка образующей описывает окруж­ность, плоскость которой перпендикулярна оси. Соответственно линия пересечения поверхности вра­щения любой плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями. Наибольшую параллель из двух соседних с нею параллелей по обе стороны от нее называют экватором, анало­гично наименьшую — горлом.

Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхно­стью вращения — меридианом. Если ось поверхности параллельна плоскости проекций, то меридиан, лежащий в плоскости, параллельной этой плоскости проекций, называют главным меридианом. На эту плоскость проекций главный меридиан проецируется без искажений.

Наиболее удобными для выполнения изображений поверх­ностей вращения являются случаи, когда их оси перпендику­лярны к плоскости Н, к плоскости V или к плоскости W.

Некоторые поверхности вращения являются частными слу­чаями поверхностей, рассмотренных ранее, например цилиндр вращения, конус вращения. Для цилиндра и конуса вращения меридианами являются прямые линии. Они параллельны оси и равноудалены от нее для цилиндра или пересекают ось в од­ной и той же ее точке под одним и тем же углом к оси для конуса. Цилиндр и конус вращения — поверхности, беско­нечные в направлении их образующих; поэтому на изображе­ниях их ограничивают какими-либо линиями, например линиями пересечения этих поверхностей с плоскостями проек­ций или какими-либо из параллелей. Из стереометрии извест­но, что прямой круговой цилиндр и прямой круговой конус ограничены поверхностью вращения и плоскостями, перпен­дикулярными к оси поверхности. Меридиан такого цилинд­ра — прямоугольник, конуса — треугольник.

 

 

Рисунок 58

Такая поверхность вращения, как сфера, является ограни­ченной и может быть изображена на чертеже полностью. Эква­тор и меридианы сферы — равные между собой окружности. При ортогональном проецировании на все три плоскости про­екций очертания сферы проецируются в окружность.

При вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, получается поверхность с названием тор. На ри­сунке 59 приведены: открытый тор, или круговое кольцо, — рисунок 59, а, закрытый тор — рисунок 59, б, самопересека­ющийся тор — рисунок 59, в, г. Тор (рис. 59, г) называют также лимоновидным. На рисунке 59 они изображены в по­ложении, когда ось тора перпендикулярна к плоскости про­екций Н. В открытый и закрытый торы могут быть вписаны сферы. Тор можно рассматривать как поверхность, огибаю­щую одинаковые сферы, центры которых находятся на ок­ружности.

В построениях на чертежах широко используют две системы круговых сечений тора: в плоскостях, перпендикулярных к его оси, и в плоскостях, проходящих через ось тора. При этом в плоскостях, перпендикулярных к оси тора, в свою очередь имеются два семейства окружностей — линий пересечения плоскостей с наружной поверхностью тора и линий пересечения плоскостей с внутренней поверхностью тора. У лимоновидного тора имеется только первое семейство окружностей. Кроме того, тор имеет еще и третью систему круговых сече­ний, которые лежат в плоскостях, проходящих через центр тора и касательных к его внутренней поверхности.

 

Рисунок 59

 

Точки на поверхности вращения. Положение точки на по­верхности вращения определяют по принадлежности точки ли­нии каркаса поверхности, т. е. с помощью окружности, проходящей через эту точку на поверхности вращения. В слу­чае линейчатых поверхностей для этой цели возможно приме­нение и прямолинейных образующих. Применение параллели и прямолинейной образующей для построения проекций точек, принадлежащих данной поверхности вращения, показано на рисунке 60.

Рисунок 60 Рисунок 61

 

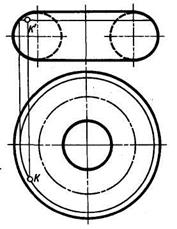
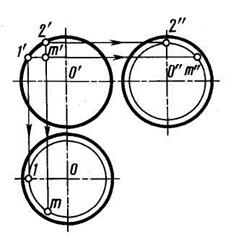
На рисунке 60 показано построение проекций точки К, принадлежащей поверхности тора. Следует отметить, что по­строение выполнено для видимых горизонтальной проекции к и фронтальной проекции к'.

На рисунке 61 показано построение по заданной фрон­тальной проекции т' точки на поверхности сферы ее гори­зонтальной т и профильной т" проекций. Проекция т построена с помощью окружности — параллели, проходящей через проекцию т'. Ее радиус о – 1. Проекция т" постро­ена с помощью окружности, плоскость которой параллельна профильной плоскости проекций, проходящей через проек­цию т'. Ее радиус о"2".