Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

 

а) модель	б) эпюр
Рисунок 20. Скрещивающиеся прямые

 

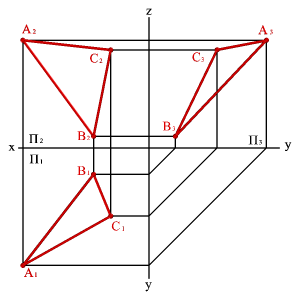
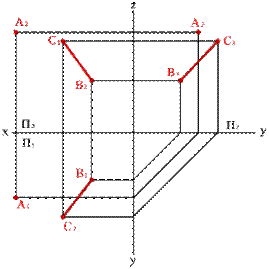
Точке пересечения фронтальных проекций прямых (рис.20) соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично).

Этот способ определения видимости по конкурирующим точкам. В данном случае точки А и В - фронтально конкурирующие, а С и D - горизонтально конкурирующие.

ПРОЕКЦИИ ПЛОСКОСТИ

3.1. Способы задания плоскости на чертеже

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис. 21);

 

а) модель	б) эпюр
Рисунок 21. Плоскость, заданная тремя точками, не лежащими на одной прямой

2. прямой линией и точкой, не принадлежащей этой прямой (рис. 22);

3. двумя пересекающимися прямыми (рис. 23);

4. двумя параллельными прямыми (рис. 24);

 

 

 

а) модель	б) эпюр
Рисунок 22. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии
а) модель	б) эпюр
Рисунок 23. Плоскость, заданная двумя пересекающимися прямыми
а) модель	б) эпюр
Рисунок 24. Плоскость, заданная двумя параллельными прямыми

5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис. 25).

Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная плоскость различают горизонтальный, фронтальный и профильный следы.

а) модель	б) эпюр
Рисунок 25. Плоскость, заданная следами

 

Следы плоскости общего положения пересекаются попарно на осях в точках a_x,a_y,a_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

 

Точка и прямая в плоскости

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.

Если точка принадлежит плоскости, то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.