Взаимное пересечение поверхностей

 

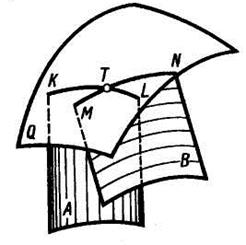
Форма большинства сложных и ответствен­ных деталей приборов и машин образована комбинацией раз­личных элементарных тел, расположенных в пространстве так, что поверхности их пересекаются между собой. Поэтому важ­ным этапом конструирования таких деталей является определе­ние границ исходных поверхностей, которыми и являются линии их взаимного пересечения.

В общем случае линию пересечения двух повер­хностей между собой строят по точкам, которые находят спомощью вспомогательных секущих по­верхностей (или плоскостей).

Две криволинейные поверхности А и В (рисунок 69) пересекаются тре­тьей секущей вспомогательной повер­хностью Q. Находят линии пересе­чения KL и MN вспомогательной поверхности с каждой из заданных. Точка Т пересечения построенных линий KL и MN принадлежит линии пересечения заданных поверхностей А и В. Повторяя такие построения многократно с помощью ана­логичных вспомогательных поверхностей, находят необходи­мое число общих точек двух поверхностей для проведения линии ихпересечения.

Сформулируем общее правило построения линии пересече­ния поверхностей:

– выбирают вид вспомогательных поверхностей;

– строят линии пересечения вспомогательных поверхностей с заданными поверхностями;

– находят точки пересечения построенных линий и соединяют их между собой плавной кривой.

 

Рисунок 69

Способ вспомогательных секущих плоскостей. Рассмотрим применение вспомогательных секущих плоско­стей на примере построения линии пересечения сферы с кону­сом вращения (рисунок 70).

Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси ко­нуса, которые пересекают сферу и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.

Построение начинают обычно с отыскания проекций ха­рактерных точек. Проекции 1' высшей и 2' низшей точек явля­ются точками пересечения фронтальных проекций очерков, так как центр сферы и ось конуса лежат в плоскости, параллель­ной плоскости V. Их горизонтальные 1, 2 ипрофильные 1", 2" проекции находят в проекционной связи. Проекции 3', 3, 3" и 4', 4, 4", лежащие на экваторе сферы, находят с помощью горизонтальной плоскости Q (Q_v), проходящей через центр сферы О (о'). Она пересекает сферу по экватору и конус по окружности радиуса r_q, в пересечении горизонтальных проек­ций которых и находят горизонтальные проекции 3, 4 точек искомой линии пересечения. Горизонтальные проекции 3 и 4 этих точек являются границами видимости участков линии пе­ресечения на этой проекции. Проекции промежуточных точек, например 5', 5, 5" и 6', 6, 6", находят с помощью вспомога­тельной горизонтальной плоскости Т(T_v). Их построение ясно из чертежа. Аналогично построены другие точки. Профиль­ные проекции точек линии пересечения строят по их фрон­тальной и горизонтальной проекциям. Точки с проекциями 7', 7, 7" и 8', 8, 8" являются границами видимости участков профильной проекции линии пересечения. Ниже проекций 7" и 8" профильная проекция линии пересечения видима. Точ­ное построение проекций этих точек см. на рисунке 70.

 

 

 

Рисунок 70

 

Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями.

 

Рисунок 71

Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа, в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рисунке 71) или одна из осей становиться проецирующей прямой, а вторая – линией уровня.

Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.71). Эта точка принимается за центр всех вспомогательных концентрических сфер. Каждая из концентрических сфер пересекает поверхности по окружностям – параллелям (а, b, c, d, n), фронтальные проекции которых являются прямыми линиями (а ₂, b ₂, c ₂, d ₂, n ₂). Проекции точек 1 ₂, 2 ₂, 3 ₂, 4 ₂, 5 ₂ и 6 ₂ пересечения проекций параллелей принадлежат проекции искомой линии пересечения поверхностей. Пересечение главных фронтальных меридианов поверхностей определяют положение верхней и нижней точек (7 и 8)линии.

Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны видимости линии пересечения поверхностей на горизонтальной проекции. Для этой цели использовалась вспомогательная секущая плоскость, которая пересекает поверхность Q по линии m, а поверхность G по образующим, горизонтальные проекции которых пересекаясь определяют положение искомых точек.

Соединив найденные точки 1... 10 с учетом видимости получим линию пересечения поверхностей.

 

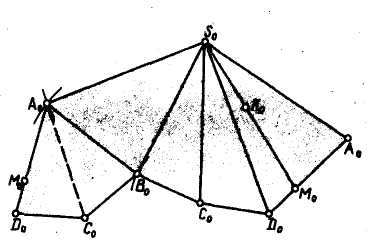
РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Развертка пирамиды. Развертка пи­рамиды осуществляется в следующем по­рядке:

а) определяют истинную величину всех ребер пирамиды любым из известных спо­собов. На рис. 72 способом вращения найдена длина боковых ребер и способом замены плоскостей проекций определено основание пирамиды;

б) по найденным трем сторонам (рис. 73) строят какую-либо из боковых граней, например SoAoBo, пристраивая к ней следующую SoBoCo, а затем и осталь­ные грани (масштаб развертки уменьшен);

в) достраивают основание пирамиды A₀B_oC_oD_o.

Точки, расположенные внутри контура развертки, находятся во взаимно одноз­начном соответствии с точками поверхно­сти многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. При­мером первой пары точек на рисунках слу­жат точки Ко, а иллюстрацией второго случая являются точки М и Мо.

Для определения точки Ко на развертке пришлось по ее ортогональным проекциям (рис. 74) найти длины отрезков AM (спо­собом замены плоскостей проекций) и SK (способом вращения). Эти отрезки и были использованы затем при построении на развертке сначала прямой SoMo и, нако­нец, точки Ко.

Рисунок 72

 

 

 

Рисунок 73

 

Развертки цилиндрической и конической поверхностей. Развертка цилиндрической поверхности выполняется аналогично развертке при­змы. Предварительно в заданный цилиндр вписывают n -угольную призму.

На рис. 74 выполнена развертка на­клонного эллиптического цилиндра. Так как нижнее основание его параллельно горизонтальной плоскости проекций, то для построения развертки использован способ раскатки. Параллельность образующих цилиндра горизонтальной плоскости проекций делает возможным выпол­нить развертку без предварительного пре­образования проекций.

 

 

Рисунок 74

 

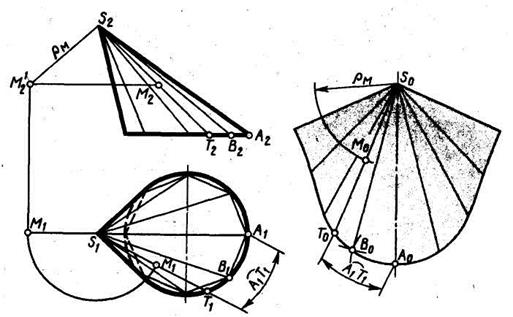
Развертка конической поверхности вы­полняется аналогично развертке пирами­ды в следующем порядке. Сначала в за­данный конус вписывают n -угольную пи­рамиду (число п, зависящее от размеров и масштаба чертежа, следует брать в пре­делах от 8 до 12). Затем строят развертку боковой поверхности вписанной пирамиды. Соединив концы ребер плавной кривой, получают прибли­женную, развертку боковой поверхности конуса.

На рис. 75 выполнено построение раз­вертки наклонного эллиптического конуса, заданного круговым основанием, лежа­щим в горизонтальной плоскости, и вер­шиной S. Истинная величина боковых ре­бер вписанной восьмиугольной пирамиды найдена способом вращения. Точка М, лежащая на поверхности конуса, перене­сена на развертку так же, как и при раз­вертке пирамиды.

 

 

Рисунок 75